顺次差1 的几个整数叫做连续数。
顺次差2的几个偶数叫做连续偶数。
顺次差2的几个奇数叫做连续奇数。
已知几个连续数的和,求这几个连续数各是多少的应用题。叫做连续数问题。
连续数的每一个数叫一项。最前面的项叫首项,最后面的项叫末项,转眼间的项叫中项。各个项数的和叫总和。
它的计算方法是:
{和–[1+2+3+……+(项数–1)]}÷项数=最小项(首项)
{和+[1+2+3+……+(项数–1)]}÷项数=最大项(末项)
总和÷项数=中间项(中项)
(首项+末项)×项数÷2=总和
例1、 7个连续自然数的和是84,这7个数各是多少?
可以先求最大数,也可以先求最小数,还可以先求中间数。
解法一:先求最大数:
(84+1+2+3+4+5+6)÷7=15
连续的各数是:9、10、11、12、13、14、15。
解法二:(84-1-2-3-4-5-6)÷7=9
连续的各数是:9、10、11、12、13、14、15
解法三:当连续数的个数是奇数时,一般可以先求中间数。
84÷7=12
连续的各数是:9、10、11、12、13、14、15
例2、 6个连续偶数的和是150,这6个偶数各是多少?
解法一:先求最大数:(150+2+4+6+8+10)÷6=30
6个连续偶数是:20、22、24、26、28、30。
解法二:先求最小数(150-2-4-6-8-10)=20
6个连续偶数是:20、22、24、26、28、30。
例3、 有七个连续奇数,第七个数是第二个数的3倍。求各数。
第七个数比第二个数大2×(7-2)=10,第七个数是第二个数的3倍,根据“差倍应用题”的计算方法,就可先求得第二个数。
[2×(7-2)]÷[3-1]=5
七个连续奇数是:3、5、7、9、11、13、15。
例4、 有七张电影票,座号是连续的单号。其座号的和是49,这些票各是多少号?
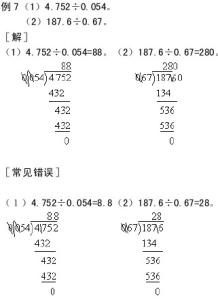
解法一:先求最大号:
(49+2+4+6+8+10+12)÷7=13
七个连续的单号是:1、3、5、7、9、11、13。
解法二:先求最小号
解法三先求中间号:(略)
 爱华网
爱华网