这部分内容在考试中一般很少单独考查,只是融合在各个题型的一些运算中,难度不大,属于容易题,但大家仍然不要忽略数学第2章指数函数对数函数和幂函数的知识点。以下是小编为您整理的关于高一数学第2章指数函数对数函数和幂函数知识点的相关资料,希望对您有所帮助。
高一数学第2章指数函数对数函数和幂函数知识点一
指数函数
指数函数是数学中重要的函数。应用到值e上的这个函数写为exp(x)。还可以等价的写为ex,这里的e是数学常数,就是自然对数的底数,近似等于 2.718281828,还称为欧拉数。
1、指数函数的定义
指数函数的一般形式为y=a^x(a>0且≠1) (x∈R).
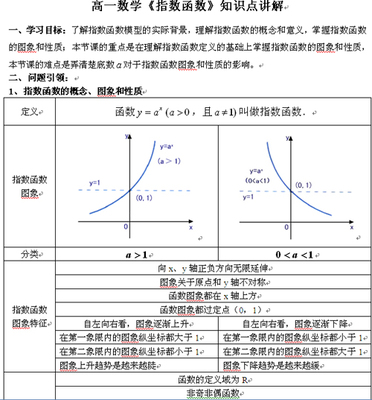
2、指数函数的性质
1.曲线沿x轴方向向左无限延展〈=〉函数的定义域为(-∞,+∞)
2.曲线在x轴上方,而且向左或向右随着x值的减小或增大无限靠近X轴(x轴是曲线的渐近线)〈=〉函数的值域为(0,+∞)
高一数学第2章指数函数对数函数和幂函数知识点二
对数函数
对数公式是数学中的一种常见公式,如果a^x=N(a>0,且a≠1),则x叫做以a为底N的对数,记做x=log(a)(N),其中a要写于log右下。
1.对数
(1)对数的定义:
如果ab=N(a>0,a≠1),那么b叫做以a为底N的对数,记作logaN=b.
(2)指数式与对数式的关系:ab=NlogaN=b(a>0,a≠1,N>0).两个式子表示的a、b、N三个数之间的关系是一样的,并且可以互化.
(3)对数运算性质:
①loga(MN)=logaM+logaN.
②loga(M/N)=logaM-logaN.
③logaMn=nlogaM.(M>0,N>0,a>0,a≠1)
④对数换底公式:logbN=(logab/logaN)(a>0,a≠1,b>0,b≠1,N>0).
2.对数函数
(1)对数函数的定义
函数y=logax(a>0,a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).
注意:真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零,底数则要大于0且不为1
对数函数的底数为什么要大于0且不为1呢?
在一个普通对数式里 a<0,或=1 的时候是会有相应b的值的。但是,根据对数定义: logaa=1;如果a=1或=0那么logaa就可以等于一切实数(比如log1 1也可以等于2,3,4,5,等等)第二,根据定义运算公式:loga M^n = nloga M 如果a<0,那么这个等式两边就不会成立 (比如,log(-2) 4^(-2) 就不等于(-2)*log(-2) 4;一个等于1/16,另一个等于-1/16
(2)对数函数的性质:
①定义域:(0,+∞).
②值域:R.
③过点(1,0),即当x=1时,y=0.
④当a>1时,在(0,+∞)上是增函数;当0
高一数学第2章指数函数对数函数和幂函数知识点三
幂函数
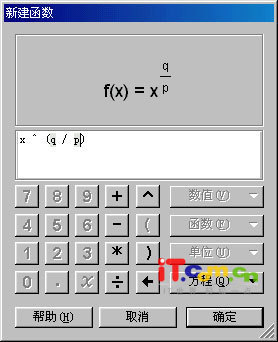
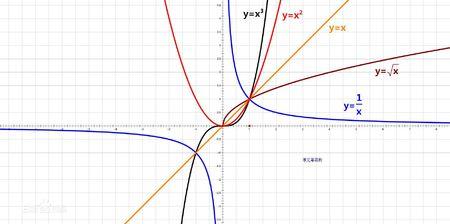
一般地,形如y=xα(α为实数)的函数,即以底数为自变量,幂为因变量,指数为常数的函数称为幂函数。例如函数y=x0 、y=x1、y=x2、y=x-1(注:y=x-1=1/x y=x0时x≠0)等都是幂函数。
定义:
形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
定义域和值域:
当a为不同的数值时,幂函数的定义域的不同情况如下:如果a为任意实数,则函数的定义域为大于0的所有实数;如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根[据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;如果同时q为奇数,则函数的定义域为不等于0的所有实数。当x为不同的数值时,幂函数的值域的不同情况如下:在x大于0时,函数的值域总是大于0的实数。在x小于0时,则只有同时q为奇数,函数的值域为非零的实数。而只有a为正数,0才进入函数的值域
 爱华网
爱华网