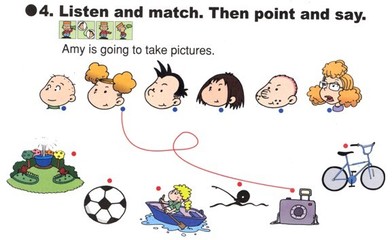
以钟表上的时针和分针行走的速度、时间、距离等方面计算为内容的应用题,叫做时钟问题。
时钟问题可以理解为分针追时针的追及问题。解答这类问题的关键就是求“速度差”。
分针走60格的同时,时针只走了5格。也就是分针走一格,时针走 = 格。分针每分钟比时针多走1– = 格。这个速度差是固定不变的。
例1、 现在是下午4时正,5时以前时针与分针正好重合的时刻是几时几分?
这是分针追及时针的问题。4时正,分针在时针后20小格,两针重合的时刻也就是分针追上时针的时刻。分针与时针的速度差为每分钟1– 格。
20÷(1– )= 分
例2、 现在是下午1时,再过多少时间,时针与分针第一次成直线(反方向)?
时针与分针成直线时,两针两针之间差30格。1点钟时,分针还在时针的后面,这时两针不可能成直线。显然,分针必须在越过时针后,才能出现两针成直线的情况。也就是说,从1点起,分针必须比时针多走(5+30)=35格
(5+30)÷(1- )= 分
例3、 2点与3点之间,时钟的两针第一次成直角的时刻是几时几分?
两针成直角时,两针之间相差15格,2点时,分针落后时针10格,必须让分针赶上时针,并超过时针15格,才能成直角,也就是说,分针要比时针多走10+15=25格。
10+15÷(1- )= 分
例4、 时钟的时针和分针由第一次成反方向开始到第二次再成反方向为止,中间一共需要多少时间?
第一次成反方向时,分针落后(或超过)时针30格,到第二次再成反方向时,分针必须比时针多走30+30=60格
(30+30)÷(1- )=65 分=1时5分 秒
例5、 9时与10时之间,时针与分针正好成60度角,这时候的时间是多少?
60度即钟盘上10格。有两种情况:
1、 分针与时针重合以前成60度角。9时,两针相差45格。即分针要比时针多走45-10=35格
(45-10)÷(1- )= 分
2、 分针与时针重合以后成60度角。分针要比时针多走45+10=55格
(45+10)÷(1- )=60分
例6、 两针正好成60度角的时刻是5点40分,不需多少时间两针第一次重合?
解法一:可以考虑两针从现在时刻到第一次重合的路程差及速度差,直接求出所需时间。
1、 两针的路程差。
20+30- ×20= 格
2、 所需时间
÷(1- )= 分
综合算式
(20+30- ×20)÷(1- )= 分
解法二:
将问题转化为:先求出从6时正开始到第一次重合所需时间然后加上前面的20分钟。
1、 从6时至两针重合所需时间。
30÷(1- )= 分

2、 从5时40分至两针重合所需时间
20+ = 分
 爱华网
爱华网