关键的八年级数学期末考试就临近了,只要努力过、奋斗过,就不会后悔。下面是小编为大家精心整理的八年级数学上册期末试卷,仅供参考。
八年级数学上册期末试题
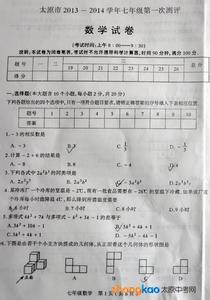
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,第1-8小题选对每小题得3分,第9-12小题选对每小题得4分,选错、不选或选出的答案超过一个均记零分.
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A.a+a=a2 B.a3•a2=a5 C.2 =2 D.a6÷a3=a2
3. 的平方根是( )
A.2 B.±2 C. D.±
4.用科学记数法表示﹣0.00059为( )
A.﹣59×10﹣5 B.﹣0.59×10﹣4 C.﹣5.9×10﹣4 D.﹣590×10﹣7
5.使分式 有意义的x的取值范围是( )
A.x≤3 B.x≥3 C.x≠3 D.x=3
6.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
7.若 有意义,则 的值是( )
A. B.2 C. D.7
8.已知a﹣b=1且ab=2,则式子a+b的值是( )
A.3 B.± C.±3 D.±4
9.如图所示,平行四边形ABCD的周长为4a,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长是( )
A.a B.2a C.3a D.4a
10.已知xy<0,化简二次根式y 的正确结果为( )
A. B. C. D.
11.如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )
A. B. C.2 D.
12.若关于x的分式方程 无解,则常数m的值为( )
A.1 B.2 C.﹣1 D.﹣2
二、填空题:本大题共4小题,共16分,只要求填写最后结果,每小题填对得4分.
13.将xy﹣x+y﹣1因式分解,其结果是 .
14.腰长为5,一条高为3的等腰三角形的底边长为 .
15.若x2﹣4x+4+ =0,则xy的值等于 .
16.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C= 度.
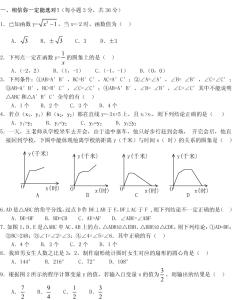
三、解答题:本大题共6小题,共64分。解答时要写出必要的文字说明、证明过程或演算步骤。
17.如图所示,写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标,并画出△ABC关于y对称的△A2B2C2.
18.先化简,再求值:
(1)5x2﹣(y+x)(x﹣y)﹣(2x﹣y)2,其中x=1,y=2.
(2)( )÷ ,其中a= .
19.列方程,解应用题.
某中学在莒县服装厂订做一批棉学生服,甲车间单独生产3天完成总量的 ,这时天气预报近期要来寒流,需要加快制作速度,这时增加了乙车间,两个车间又共同生产两天,完成了全部订单,如果乙车间单独制作这批棉学生服需要几天?
20.△ABC三边的长分别为a、b、c,且满足a2﹣4a+b2﹣4 c=4b﹣16﹣c2,试判定△ABC的形状,并证明你的结论.
21.如图,四边形ABCD是平行四边形,并且∠BCD=120°,CB=CE,CD=CF.
(1)求证:AE=AF;
(2)求∠EAF的度数.
22.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2 =(1+ )2,善于思考的小明进行了以下探索:
设a+b =(m+n )2(其中a、b、m、n均为整数),则有a+b =m .
a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b 的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n )2,用含m、n的式子分别表示a,b,得a= ,b= .
(2)利用所探索的结论,用完全平方式表示出: = .
(3)请化简: .
八年级数学上册期末试卷参考答案
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,第1-8小题选对每小题得3分,第9-12小题选对每小题得4分,选错、不选或选出的答案超过一个均记零分.
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
【考点】轴对称图形.
【分析】根据轴对称图形的概念求解.
【解答】解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
2.下列运算正确的是( )
A.a+a=a2 B.a3•a2=a5 C.2 =2 D.a6÷a3=a2
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;二次根式的加减法.
【分析】根据合并同类项、同底数幂的乘法、除法,即可解答.
【解答】解:A、a+a=2a,故错误;
B、a3•a2=a5,正确;
C、 ,故错误;
D、a6÷a3=a3,故错误;
故选:B.
【点评】本题考查了合并同类项、同底数幂的乘法、除法,解决本题的关键是熟记合并同类项、同底数幂的乘法、除法.
3. 的平方根是( )
A.2 B.±2 C. D.±
【考点】算术平方根;平方根.
【专题】常规题型.
【分析】先化简 ,然后再根据平方根的定义求解即可.
【解答】解:∵ =2,
∴ 的平方根是± .
故选D.
【点评】本题考查了平方根的定义以及算术平方根,先把 正确化简是解题的关键,本题比较容易出错.
4.用科学记数法表示﹣0.00059为( )
A.﹣59×10﹣5 B.﹣0.59×10﹣4 C.﹣5.9×10﹣4 D.﹣590×10﹣7
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:﹣0.00059=﹣5.9×10﹣4,
故选:C.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
5.使分式 有意义的x的取值范围是( )
A.x≤3 B.x≥3 C.x≠3 D.x=3
【考点】分式有意义的条件.
【分析】分式有意义的条件是分母不等于零,从而得到x﹣3≠0.
【解答】解:∵分式 有意义,
∴x﹣3≠0.
解得:x≠3.
故选:C.
【点评】本题主要考查的是分式有意义的条件,掌握分式有意义时,分式的分母不为零是解题的关键.
6.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
【考点】平行四边形的判定.
【分析】根据平行四边形判定定理进行判断.
【解答】解:A、由“AB∥DC,AD∥BC”可知,四边形ABCD的两组对边互相平行,则该四边形是平行四边形.故本选项不符合题意;
B、由“AB=DC,AD=BC”可知,四边形ABCD的两组对边相等,则该四边形是平行四边形.故本选项不符合题意;
C、由“AO=CO,BO=DO”可知,四边形ABCD的两条对角线互相平分,则该四边形是平行四边形.故本选项不符合题意;
D、由“AB∥DC,AD=BC”可知,四边形ABCD的一组对边平行,另一组对边相等,据此不能判定该四边形是平行四边形.故本选项符合题意;
故选D.
【点评】本题考查了平行四边形的判定.
(1)两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
7.若 有意义,则 的值是( )
A. B.2 C. D.7
【考点】二次根式有意义的条件.
【分析】根据二次根式中的被开方数必须是非负数求出x的值,根据算术平方根的概念计算即可.
【解答】解:由题意得,x≥0,﹣x≥0,
∴x=0,
则 =2,
故选:B.
【点评】本题考查的是二次根式有意义的条件以及算术平方根的概念,掌握二次根式中的被开方数必须是非负数是解题的关键.
8.已知a﹣b=1且ab=2,则式子a+b的值是( )
A.3 B.± C.±3 D.±4
【考点】完全平方公式.
【专题】计算题;整式.
【分析】把a﹣b=1两边平方,利用完全平方公式化简,将ab=2代入求出a2+b2的值,再利用完全平方公式求出所求式子的值即可.
【解答】解:把a﹣b=1两边平方得:(a﹣b)2=a2+b2﹣2ab=1,
将ab=2代入得:a2+b2=5,
∴(a+b)2=a2+b2+2ab=5+4=9,
则a+b=±3,
故选C
【点评】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.
9.如图所示,平行四边形ABCD的周长为4a,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长是( )
A.a B.2a C.3a D.4a
【考点】平行四边形的性质.
【分析】由▱ABCD的周长为4a,可得AD+CD=2a,OA=OC,又由OE⊥AC,根据线段垂直平分线的性质,可证得AE=CE,继而求得△DCE的周长=AD+CD.
【解答】解:∵▱ABCD的周长为4a,
∴AD+CD=2a,OA=OC,
∵OE⊥AC,
∴AE=CE,
∴△DCE的周长为:CD+DE+CE=CD+DE+AE=CD+AD=2a.
故选:B.
【点评】此题考查了平行四边形的性质以及线段垂直平分线的性质.注意得到△DCE的周长=AD+CD是关键.
10.已知xy<0,化简二次根式y 的正确结果为( )
A. B. C. D.
【考点】二次根式的性质与化简.
【分析】先求出x、y的范围,再根据二次根式的性质化简即可.
【解答】解:∵要使 有意义,必须 ≥0,
解得:x≥0,
∵xy<0,
∴y<0,
∴y =y• =﹣ ,
故选A.
【点评】本题考查了二次根式的性质的应用,能正确根据二次根式的性质进行化简是解此题的关键.
11.如图,小将同学将一个直角三角形的纸片折叠,A与B重合,折痕为DE,若已知AC=4,BC=3,∠C=90°,则EC的长为( )
A. B. C.2 D.
【考点】翻折变换(折叠问题).
【分析】DE是边AB的垂直平分线,则AE=BE,设AE=x,在直角△BCE中利用勾股定理即可列方程求得x的值,进而求得EC的长.
【解答】解:∵DE垂直平分AB,
∴AE=BE,
设AE=x,则BE=x,EC=4﹣x.
在直角△BCE中,BE2=EC2+BC2,则x2=(4﹣x)2+9,
解得:x= ,
则EC=AC﹣AE=4﹣ = .
故选B.
【点评】本题考查了图形的折叠的性质以及勾股定理,正确理解DE是AB的垂直平分线是本题的关键.
12.若关于x的分式方程 无解,则常数m的值为( )
A.1 B.2 C.﹣1 D.﹣2
【考点】分式方程的解;解一元一次方程.
【专题】计算题;转化思想;一次方程(组)及应用;分式方程及应用.
【分析】将分式方程去分母化为整式方程,由分式方程无解得到x=3,代入整式方程可得m的值.
【解答】解:将方程两边都乘以最简公分母(x﹣3),得:1=2(x﹣3)﹣m,
∵当x=3时,原分式方程无解,
∴1=﹣m,即m=﹣1;
故选C.
【点评】本题主要考查分式方程的解,对分式方程无解这一概念的理解是此题关键.
二、填空题:本大题共4小题,共16分,只要求填写最后结果,每小题填对得4分.
13.将xy﹣x+y﹣1因式分解,其结果是 (y﹣1)(x+1) .
【考点】因式分解-分组分解法.
【分析】首先重新分组,进而利用提取公因式法分解因式得出答案.
【解答】解:xy﹣x+y﹣1
=x(y﹣1)+y﹣1
=(y﹣1)(x+1).
故答案为:(y﹣1)(x+1).
【点评】此题主要考查了分组分解法分解因式,正确分组是解题关键.
14.腰长为5,一条高为3的等腰三角形的底边长为 8或 或3 .
【考点】等腰三角形的性质;三角形三边关系.
【分析】根据不同边上的高为3分类讨论,利用勾股定理即可得到本题的答案.
【解答】解:①如图1.
当AB=AC=5,AD=3,
则BD=CD=4,
所以底边长为8;
②如图2.
当AB=AC=5,CD=3时,
则AD=4,
所以BD=1,
则BC= = ,
即此时底边长为 ;
③如图3.
当AB=AC=5,CD=3时,
则AD=4,
所以BD=9,
则BC= =3 ,
即此时底边长为3 .
故答案为:8或 或3 .
【点评】本题考查了等腰三角形的性质,勾股定理,解题的关键是分三种情况分类讨论.
15.若x2﹣4x+4+ =0,则xy的值等于 6 .
【考点】解二元一次方程组;非负数的性质:偶次方;非负数的性质:算术平方根;配方法的应用.
【专题】计算题;一次方程(组)及应用.
【分析】已知等式变形后,利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可确定出xy的值.
【解答】解:∵x2﹣4x+4+ =(x﹣2)2+ =0,
∴ ,
解得: ,
则xy=6.
故答案为:6
【点评】此题考查了解二元一次方程组,配方法的应用,以及非负数的性质,熟练掌握运算法则是解本题的关键.
16.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C= 180 度.
【考点】勾股定理的逆定理;勾股定理.
【分析】勾股定理的逆定理是判定直角三角形的方法之一.
【解答】解:连接AC,根据勾股定理得AC= =25,
∵AD2+DC2=AC2即72+242=252,
∴根据勾股定理的逆定理,△ADC也是直角三角形,∠D=90°,
故∠A+∠C=∠D+∠B=180°,故填180.
【点评】本题考查了勾股定理和勾股定理的逆定理,两条定理在同一题目考查,是比较好的题目.
三、解答题:本大题共6小题,共64分。解答时要写出必要的文字说明、证明过程或演算步骤。
17.如图所示,写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标,并画出△ABC关于y对称的△A2B2C2.
【考点】作图-轴对称变换.
【分析】分别利用关于x轴、y轴对称点的坐标性质得出各对应点的位置,进而得出答案.
【解答】解:△ABC各顶点的坐标以及△ABC关于x轴对称的△A1B1C1的各顶点坐标:
A1(﹣3,﹣2),B1(﹣4,3),C1(﹣1,1),
如图所示:△A2B2C2,即为所求.
【点评】此题主要考查了轴对称变换,得出对应点位置是解题关键.
18.先化简,再求值:
(1)5x2﹣(y+x)(x﹣y)﹣(2x﹣y)2,其中x=1,y=2.
(2)( )÷ ,其中a= .
【考点】分式的化简求值;整式的混合运算—化简求值.
【分析】(1)先根据整式混合运算的法则把原式进行化简,再把x、y的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
【解答】解:(1)原式=5x2﹣x2+y2﹣4x2+4xy﹣y2
=4xy,
当x=1,y=2时,原式=4×1×2=8;
(2)原式= •
= •
=a﹣1,
当a= 时,原式= ﹣1.
【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
19.列方程,解应用题.
某中学在莒县服装厂订做一批棉学生服,甲车间单独生产3天完成总量的 ,这时天气预报近期要来寒流,需要加快制作速度,这时增加了乙车间,两个车间又共同生产两天,完成了全部订单,如果乙车间单独制作这批棉学生服需要几天?
【考点】分式方程的应用.
【分析】设乙车间单独制作这批棉学生服需要x天,则每天能制作总量的 ;甲车间单独生产3天完成总量的 ,则每天能制作总量的 ,根据总的工作量为1列出方程并解答.
【解答】解:设乙车间单独制作这批棉学生服需要x天,则每天能制作总量的 ;甲车间单独生产3天完成总量的 ,则每天能制作总量的 ,
根据题意,得: +2×( + )=1,
解得x=4.5.
经检验,x=4.5是原方程的根.
答:乙车间单独制作这批棉学生服需要4.5天.
【点评】本题考查了分式方程的应用.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.
20.△ABC三边的长分别为a、b、c,且满足a2﹣4a+b2﹣4 c=4b﹣16﹣c2,试判定△ABC的形状,并证明你的结论.
【考点】因式分解的应用.
【分析】根据完全平方公式,可得非负数的和为零,可得每个非负数为零,可得a、b、c的值,根据勾股定理逆定理,可得答案.
【解答】解:△ABC是等腰直角三角形.
理由:∵a2﹣4a+b2﹣4 c=4b﹣16﹣c2,
∴(a2﹣4a+4)+(b2﹣4b+4)+(c2﹣4 c+8)=0,
即:(a﹣2)2+(b﹣2)2+(c﹣2 )2=0.
∵(a﹣2)2≥0,(b﹣2)2≥0,(c﹣2 )2≥0,
∴a﹣2=0,b﹣2=0,c﹣2 =0,
∴a=b=2,c=2 ,
∵22+22=(2 )2,
∴a2+b2=c2,
所以△ABC是以c为斜边的等腰直角三角形.
【点评】本题考查了因式分解的应用,勾股定理逆定理,利用了非负数的和为零得出a、b、c的值是解题关键.
21.如图,四边形ABCD是平行四边形,并且∠BCD=120°,CB=CE,CD=CF.
(1)求证:AE=AF;
(2)求∠EAF的度数.
【考点】全等三角形的判定与性质;平行四边形的性质.
【分析】(1)寻找分别含有AE和AF的三角形,通过证明两三角形全等得出AE=AF.
(2)在∠BAD中能找出∠EAF=∠BAD﹣(∠BAE+∠FAD),在(1)中我们证出了三角形全等,将∠FAD换成等角∠AEB即可解决.
【解答】(1)证明:∵四边形ABCD是平行四边形,并且∠BCD=120°,
∴∠BCE=∠DCF=60°,CB=DA,CD=BA,∠ABC=∠ADC,
∵CB=CE,CD=CF,
∴△BEC和△DCF都是等边三角形,
∴CB=CE=BE=DA,CD=CF=DF=BA,
∴∠ABC+∠CBE=∠ADC+∠CDF,
即:∠ABE=∠FDA
在△ABE和△FDA中,AB=DF,∠ABE=∠FDA,BE=DA,
∴△ABE≌△FDA (SAS),
∴AE=AF.
(2)解:∵在△ABE中,∠ABE=∠ABC+∠CBE=60°+60°=120°,
∴∠BAE+∠AEB=60°,
∵∠AEB=∠FAD,
∴∠BAE+∠FAD=60°,
∵∠BAD=∠BCD=120°,
∴∠EAF=∠BAD﹣(∠BAE+∠FAD)=120°﹣60°=60°.
答:∠EAF的度数为60°.
【点评】本题考查全等三角形的判定与性质,解题的关键是寻找合适的全等三角形,通过寻找等量关系证得全等,从而得出结论.
22.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2 =(1+ )2,善于思考的小明进行了以下探索:
设a+b =(m+n )2(其中a、b、m、n均为整数),则有a+b =m .
a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b 的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n )2,用含m、n的式子分别表示a,b,得a= m2+3n2 ,b= 2mn .
(2)利用所探索的结论,用完全平方式表示出: = (2+ )2 .
(3)请化简: .
【考点】二次根式的性质与化简.
【专题】阅读型.
【分析】(1)利用已知直接去括号进而得出a,b的值;
(2)直接利用完全平方公式,变形得出答案;
(3)直接利用完全平方公式,变形化简即可.
【解答】解:(1)∵a+b =(m+n )2,
∴a+b =(m+n )2=m2+3n2+2 mn,
∴a=m2+3n2,b=2mn;
故答案为:m2+3n2;2mn;
(2) =(2+ )2;
故答案为:(2+ )2;
(3)∵12+6 =(3+ )2,
∴ = =3+ .
【点评】此题主要考查了二次根式的性质与化简,正确利用完全平方公式化简是解题关键.
 爱华网
爱华网