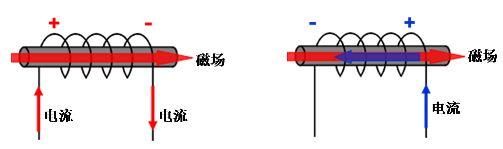
电感是闭合回路的一种属性,是一个物理量。当线圈通过电流后,在线圈中形成磁场感应,感应磁场又会产生感应电流来抵制通过线圈中的电流。以下是由小编整理关于电感基础知识的内容,希望大家喜欢!
电感的定义导体的一种性质,用导体中感生的电动势或电压与产生此电压的电流变化率之比来量度。稳恒电流产生稳定的磁场,不断变化的电流(交流)或涨落的直流产生变化的磁场,变化的磁场反过来使处于此磁场的导体感生电动势。感生电动势的大小与电流的变化率成正比。比例因数称为电感,以符号L表示,单位为亨利(H)。
电感是闭合回路的一种属性,即当通过闭合回路的电流改变时,会出现电动势来抵抗电流的改变。这种电感称为自感(self-inductance),是闭合回路自己本身的属性。假设一个闭合回路的电流改变,由于感应作用而产生电动势于另外一个闭合回路,这种电感称为互感(mutual inductance)。
自感
当线圈中有电流通过时,线圈的周围就会产生磁场。当线圈中电流发生变化时,其周围的磁场也产生相应的变化,此变化的磁场可使线圈自身产生感应电动势(感生电动势)(电动势用以表示有源元件理想电源的端电压),这就是自感。
互感
两个电感线圈相互靠近时,一个电感线圈的磁场变化将影响另一个电感线圈,这种影响就是互感。互感的大小取决于电感线圈的自感与两个电感线圈耦合的程度,利用此原理制成的元件叫做互感器。
电感的计算公式自感
一个通有电流为I的线圈(或回路),其各匝交链的磁通量的总和称作该线圈的磁链ψ。如果各线匝交链的磁通量都是Φ,线圈的匝数为N,则线圈的磁链ψ=NΦ。线圈电流I随时间变化时,磁链Ψ也随时间变化。根据电磁感应定律,在线圈中将感生自感电动势EL,其值为
定义线圈的自感L为自感电动势eL和电流的时间导数dI/dt的比值并冠以负号,即
以上二式中,ψ和eL的正方向,以及ψ和I的正方向都符合右手螺旋规则。已知电感L,就可以由dI/dt计算自感电动势。此外,自感还可定义如下
线性磁媒质下四种自感计算公式
从工程观点看,除铁磁材料以外的媒质可认为是线性磁媒质,它们的磁导率近似等于真空磁导率μ0。置于这种媒质中的线圈的自感,只和线圈及其线匝导体的形状、尺寸有关,和电流的量值无关。
四种几何形状简单的线圈或回路的自感L的计算公式如下:
(1)长螺线管的自感(忽略端部效应和线匝径向尺寸)
式中l为螺线管的长度;S为螺线管的截面积;N为总匝数。
(2)无磁芯环形密绕线圈的自感(环的截面为正方形,环的平均半径为R)
式中b为正方形截面的边长;N为总匝数。若R≫b,则近似有L≈μ0Nb/2πR,形式上与长螺线管自感计算式相同。
(3)同轴电缆的自感(忽略端部效应)
式中R1、R2分别为同轴电缆内外导体的半径;l为电缆长度;Li和Lo分别称为同轴电缆的内自感和外自>感,其中内自感Li的值仅与电缆内导体的长度有关,而与其半径无关。
(4)二线传输线的自感(忽略端部效应)
式中R为两导线的半径;l为传输线长度;D为两导线轴线间距离。
互感
设线性磁媒质中有两个相邻的线圈。线圈1中有电流I1。I1产生的与线圈2交链的那部分磁通量形成互感磁链ψ21。电流I1随时间变化时,ψ21也随之变化;由电磁感应定律,线圈2中将出现互感电动势M2
定义线圈1对线圈2的互感M21为或类似的,若线圈2中有电流I2,它产生互感磁链ψ12与线圈1交链。I2变化时,线圈1中出现互感电动势EM1
式中M12称线圈2对线圈1的互感。上式是M12的定义式。
若电流I1是恒定电流,或I1是变化率较低的时变电流,互感磁链ψ12和I1成正比,此比例系数(正常数)即线圈1对线圈2的互感M21,且
ψ21=M21I1
类似的,若电流I2是恒定电流或变化率较低的时变电流,ψ2和I2成正比,比例系数即线圈2对线圈1的互感M12,且
ψ12=M12I2
理论证明,M12=M21,用M代表它们,则
在线圈1、2中同时通以时变电流,它们分别是I1、I2时,线圈中的感应电动势e1,e2是自感电动势和互感电动势之和
线性磁媒质下二种互感计算公式
互感M不仅和线圈及其导体的形状、尺寸、真空磁导率μ0有关,还和两线圈的相互位置有关。
(1)两同轴长螺线管间的互感(忽略端部效应,近似认为两螺线管半径为同一数值R,设两螺线管长度分别为l1和l2,且l1>l2)
式中N1,N2分别为两螺线管的匝数。
(2)两对传输线间的互感(设两对二线传输线AA′和BB′相互平行,忽略端部效应及导线半径的影响)
式中DAB′、DA′B、DAB、DA′B′分别为两对传输线间相应导线间的距离,如图示;l为传输线长度。
三相制均衡输电线的电感
三根输电线之间有互感。在采用三相输电线换位技术后,各相均衡。在考虑了自感磁链和互感磁链的效应后,可得每一相两对平行的传输线输电线单位长度的等效电感L为
式中D= (DAB、DBC、DCA分别为相应相线间的距离)称几何平均距离;R为导线半径。
 爱华网
爱华网