数列作为高考的考点与热点,在历年的高考中所占比例较大,特别在综合题中的应用,能力要求越来越高。以下是小编为您整理的关于2017年高考数学数列的应用知识点的相关资料,希望对您有所帮助。
一、数列递推思想在某些概率问题方面的应用
例:已知,正四面体中,一枚棋子从一个顶点出发,选任何一条棱移动的概率都相等,每次移动前,掷一次骰子,出现偶数点,则棋子原地不动;若出现奇数点,则移动。 一枚棋子从点开始移动到点,求掷次骰子,才到达点的概率。
点拨:此题位置不确定,掷点奇偶不定,关系复杂,利用递推思想是最有郊的方法,通过构建递推数列,问题迎刃而解。一般存在相互依存关系问题的概率都可运用递推思路去解决。
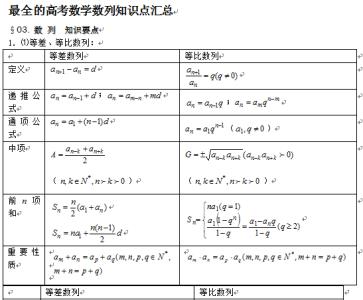
综上所述,灵活运用递推思维,构造递推数列解决某些问题,可以起到化繁为简、化抽象为具体的奇效。 其运用过程中,融高度的逻辑性于一体,是数学中化归思想的深度体现,因此在平时高考复习中,应引起我们足够的重视。
二、数列递推思想在计数方面的应用
例:将一个圆分成个扇形部分,依次为,每一扇形分别用种不同颜色中任一种涂色,其中相邻部分涂不同颜色,则不同的染色方案有多少种?
点拨:在一些复杂的计数问题中,运用数列递推思维组建递推关系可起到“疱丁解牛”的作用,使问题清晰而明了。需要说明的是,此题涉及到计数中的染色问题,通过递归关系得到一个一般化的通式,此式在染色问题中应用相当广泛。
三、数列在归纳推理中应用
例:一白珠下面挂一黑珠,每一黑珠下挂一黑珠与一白珠,则第11行黑珠的个数为________。[…第一行][…第二行][…第三行][…第四行][…第五行][…第六行]
点拨:此题通过运用递推思想得到一个递推关系,正是著名的“斐波拉契数列”。 在一些数列归纳通项的推理中,利用递推思想,构建递推公式,使有限拓展到无限,由特殊变成一般规律,这是解决此类问题常见思路与方法,同理这也体现了合理推理的精髓所在。
四、数列用递推思想解决一些浓度混合应用题
例:现有流量均为300m3/s的两条河流汇合于某处后,不断混合,它们的含沙量分别为2kg/m3和0。2kg/m3。 假设从汇合处开始,沿岸设有若干观测点,两股水流在流经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交换100m3的水量,即从股流入股100m3水,经混合后,又从股流入股100m3的水量并混合。问:从第个观测开始,两股河水的含沙量之差小于0。01kg/m3(不考虑泥沙沉淀)。
点拨:在浓度混合问题中,不断地“混合”,使问题变得较为“混沌”,此类问题可通过构建交叉递推数列,再利用递推数列的解法去化“混沌”为“清晰”,使思路明了而清晰。
 爱华网
爱华网