小学数学常用的十一种解题思路
一、直接思路
“直接思路”是解题中的常规思路。它一般是通过分析、综合、归纳等方法,直接找到解题的途径。
【顺向综合思路】从已知条件出发,根据数量关系先选择两个已知数量,提出可以解决的问题;然后把所求出的数量作为新的已知条件,与其他的已知条件搭配,再提出可以解决的问题;这样逐步推导,直到求出所要求的解为止。这就是顺向综合思路,运用这种思路解题的方法叫“综合法”。
例1 兄弟俩骑车出外郊游,弟弟先出发,速度为每分钟200米,弟弟出发5分钟后,哥哥带一条狗出发,以每分钟250米的速度追赶弟弟,而狗以每分钟300米的速度向弟弟追去,追上弟弟后,立即返回,见到哥哥后又立即向弟弟追去,直到哥哥追上弟弟,这时狗跑了多少千米?
分析(按顺向综合思路探索):
(1)根据弟弟速度为每分钟200米,出发5分钟的条件,可以求什么?
可以求出弟弟走了多少米,也就是哥哥追赶弟弟的距离。
(2)根据弟弟速度为每分钟200米,哥哥速度为每分钟250米,可以求什么?
可以求出哥哥每分钟能追上弟弟多少米。
(3)通过计算后可以知道哥哥追赶弟弟的距离为1000米,每分钟可追上的距离为50米,根据这两个条件,可以求什么?
可以求出哥哥赶上弟弟所需的时间。
(4)狗在哥哥与弟弟之间来回不断奔跑,看起来很复杂,仔细想一想,狗跑的时间与谁用的时间是一样的?
狗跑的时间与哥哥追上弟弟所用的时间是相同的。
(5)已知狗以每分钟300米的速度,在哥哥与弟弟之间来回奔跑,直到哥哥追上弟弟为止,和哥哥追上弟弟所需的时间,可以求什么?
可以求出这时狗总共跑了多少距离?
这个分析思路可以用下图(图2.1)表示。
例2 下面图形(图2.2)中有多少条线段?
分析(仍可用综合思路考虑):
我们知道,直线上两点间的一段叫做线段,如果我们把上面任意相邻两点间的线段叫做基本线段,那么就可以这样来计数。
(1)左端点是A的线段有哪些?
有 AB AC AD AE AF AG共 6条。
(2)左端点是B的线段有哪些?
有 BC、BD、BE、BF、BG共5条。
(3)左端点是C的线段有哪些?
有CD、CE、CF、CG共4条。
(4)左端点是D的线段有哪些?
有DE、DF、DG共3条。
(5)左端点是E的线段有哪些?
有EF、EG共2条。
(6)左端点是F的线段有哪些?
有FG共1条。
然后把这些线段加起来就是所要求的线段。
二、逆向分析思路
从题目的问题入手,根据数量关系,找出解这个问题所需要的两个条件,然后把其中的一个(或两个)未知的条件作为要解决的问题,再找出解这一个(或两个)问题所需的条件;这样逐步逆推,直到所找的条件在题里都是已知的为止,这就是逆向分析思路,运用这种思路解题的方法叫分析法。
例1 两只船分别从上游的A地和下游的B地同时相向而行,水的流速为每分钟30米,两船在静水中的速度都是每分钟600米,有一天,两船又分别从A、B两地同时相向而行,但这次水流速度为平时的2倍,所以两船相遇的地点比平时相遇点相差60米,求A、B两地间的距离。
分析(用分析思路考虑):
(1)要求A、B两地间的距离,根据题意需要什么条件?
需要知道两船的速度和与两船相遇的时间。
(2)要求两船的速度和,必要什么条件?
两船分别的速度各是多少。题中已告之在静水中两船都是每分钟600米,那么不论其水速是否改变,其速度和均为(600+600)米,这是因为顺水船速为:船速+水速,逆水船速为:船速-水速,故顺水船速与逆水船速的和为:船速+水速+船速-水速=2个船速(实为船在静水中的速度)
(3)要求相遇的时间,根据题意要什么条件?
两次相遇的时间因为距离相同,速度和相同,所以应该是相等的,这就是说,尽管水流的速度第二次比第一次每分钟增加了30米,仍不会改变相遇时间,只是改变了相遇地点:偏离原相遇点60米,由此可知两船相遇的时间为60÷30=2(小时)。
此分析思路可以用下图(图2.3)表示:
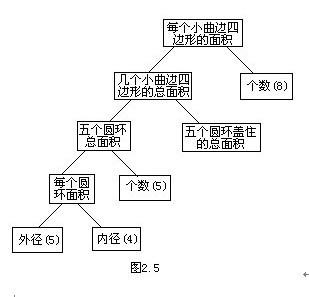
例2 五环图由内径为4,外径为5的五个圆环组成,其中两两相交的小曲边四边形(阴影部分)的面积都相等(如图2.4),已知五个圆环盖住的总面积是122.5,求每个小曲边四边形的面积(圆周率π取3.14)
分析(仍用逆向分析思路探索):
(1)要求每个小曲边四边形的面积,根据题意必须知道什么条件?
曲边四边形的面积,没有公式可求,但若知道8个小曲边四边形的总面积,则只要用8个曲边四边形总面积除以8,就可以得到每个小曲边四边形的面积了。
(2)要求8个小曲边四边形的总面积,根据题意需要什么条件?
8个小曲边四边形恰好是圆环面积两两相交重叠一次的部分,因此只要把五个圆环的总面积减去五个圆环盖住的总面积就可以了。
(3)要求五个圆环的总面积,根据题意需要什么条件?
求出一个圆环的面积,然后乘以5,就是五个圆环的总面积。
(4)要求每个圆环的面积,需要什么条件?
已知圆环的内径(4)和外径(5),然后按圆环面积公式求就是了。
圆环面积公式为:
S圆环=π(R2-r2)
=π(R+r)(R-r)
其思路可用下图(图2.5)表示:
三、一步倒推思路
顺向综合思路和逆向分析思路是互相联系,不可分割的。在解题时,两种思路常常协同运用,一般根据问题先逆推第一步,再根据应用题的条件顺推,使双方在中间接通,我们把这种思路叫“一步倒推思路”。这种思路简明实用。
例1 一只桶装满10千克水,另外有可装3千克和7千克水的两只空桶,利用这三只桶,怎样才能把10千克水分为5千克的两份?
分析(用一步倒推思路考虑):
(1)逆推第一步:把10千克水平分为5千克的两份,根据题意,关键是要找到什么条件?
因为有一只可装3千克水的桶,只要在另一只桶里剩2千克水,利用3+2=5,就可以把水分成5千克一桶,所以关键是要先倒出一个2千克水。
(2)按条件顺推。第一次:10千克水倒入7千克桶,10千克水桶剩3千克水,7千克水倒入3千克桶,7千克水桶剩4千克水,3千克水桶里有水3千克;第二次:3千克桶的水倒入10千克水桶,这时10千克水桶里有水6千克,把7千克桶里的4千克水倒入3千克水桶里,这时7千克水桶里剩水1千克,3千克水桶里有水3千克;第三次:3千克桶里的水倒入10千克桶里,这时10千克桶里有水9千克,7千克桶里的1千克水倒入3千克桶里,这时7千克桶里无水,3千克桶里有水1千克;第四次:10千克桶里的9千克水倒入7千克桶里,10千克水桶里剩下 2千克水,7千克桶里的水倒入3千克桶里(原有1千克水),只倒出2千克水,7千克桶里剩水5千克,3千克桶里有水3千克,然后把3千克桶里的3千克水倒10千克桶里,因为原有2千克水,这时也正好是5千克水了。
其思路可用下图(图2.6和图2.7)表示:
问题:
例2 今有长度分别为1、2、3……9厘米的线段各一条,可用多少种不同的方法,从中选用若干条线段组成正方形?
分析(仍可用一步倒推思路来考虑):
(1)逆推第一步。要求能用多少种不同方法,从中选用若干条线段组成正方形必须的条件是什么?
根据题意,必须知道两个条件。一是确定正方形边长的长度范围,二是每一种边长有几种组成方法。
(2)从条件顺推。
①因为九条线段的长度各不相同,所以用这些线段组成的正方形至少要7条,最多用了9条,这样就可以求出正方形边长的长度范围为(1+2+……
②当边长为7厘米时,各边分别由1+6、2+5、3+4及7组成,只有一种组成方法。
③当边长为8厘米时,各边分别由1+7、2+6、3+5及8组成,也只有一种组成方法。
④当边长为9厘米时,各边分别由1+8、2+7、3+6及9;1+8、2+7、4+5及9;2+7、3+6、4+5及9;1+8、3+6、4+5及9;1+8、2+7、3+6及4+5共5种组成方法。
⑤当边长为10厘米时,各边分别由1+9、2+8、3+7及4+6组成,也只有一种组成方法。
⑤当边长为11厘米时,各边分别由2+9、 3+8、4+7及5+6组成,也只有一种组成方法。
⑥将上述各种组成法相加,就是所求问题了。
此题的思路图如下(图2.8):
问题:
 爱华网
爱华网