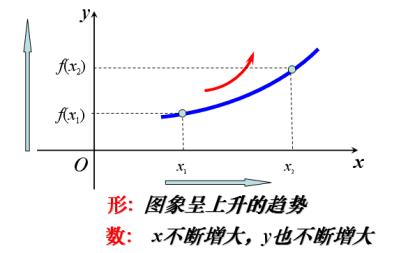
函数的单调性是函数的一个很重要的性质,也是历年高考命题的重点。但是不少同学由于对概念认识不足,审题不清,在解答这类题时容易出现错解。下面小编对函数单调性加以说明。
一、 判断函数单调性的方法
1、 定义法:利用定义严格判断
2、 利用函数的运算性质:如若f(x)、g(x)为增函数,则
(1) f(x)+g(x)为增函数;
(2) x(1)为减函数(f(x)≠0);
(3) 为增函数(f(x)≥0);
(4) f(x) ·g(x)为增函数(f(x)>0,g(x)>0);
(5) - f(x)为减函数。
3、 利用复合函数关系判断单调性。
法则是“同增异减”,即两个简单函数的单调性相同,则这两个函数的复合函数为增函数,若两个简单函数的单调性相反,则这两个函数的复合函数为减函数。
4、 图象法
5、 导数法
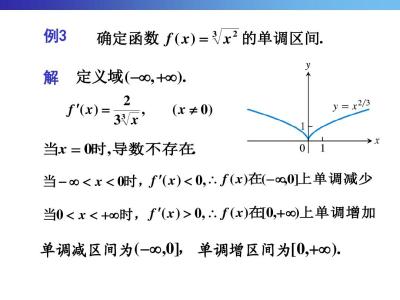
(1) 若f(x)在某个区间内可导,当f′(x)>0时,f(x)为增函数;当f′(x)<0时,f(x)为减函数;
(2) 若f(x)在某个区间内可导,当f(x)该区间上递增时,则f′(x)≥0;当f(x)该区间上递减时,f′(x)≤0。
二、 对函数单调性的理解
1、 单调性是与“区间”紧密相关的概念,一个函数在不同的区间上,可以有不同的单调性;
2、 函数的单调性只能在函数的定义域内来讨论,所以求函数的单调区间,必须先求函数的定义域。
3、 函数的单调性定义中的x1、x2有三个特征:一是任意性;二是有大小,即x1<x2(或x1>x2);三是同属于一个单调区间,三者缺一不可。
4、 由于定义域都是充要性命题,因此由f(x)是增(减)函数且f(x1)<f(x2)( f(x1)> f(x2)x1<x2
这说明单调性使得自变量间的不等关系和函数值之间的不等关系可以“互逆互推”。
5、函数的单调性是对某个区间而言的,所以要受到区间的限制。例如函数y = x(1)分别在
(-∞,0),(0,+∞)内都是单调递减的,但不能说它在整个定义域即(-∞,0)∪(0,+∞)内单调递减,只能分开写,即函数的单调区间为(-∞,0)和(0,+∞),不能用“∪”。
6、在研究函数的单调性时,常需要先将函数化简,转化为讨论一些熟知的函数的单调性,因此掌握并熟记一次函数、二次函数、指数函数、对数函数、三角函数的单调性,将大大缩短我们的判断过程。
 爱华网
爱华网