往往有同学进入高中以后不能适应数学学习,进而影响到学习的积极性,甚至成绩一落千丈。为什么会这样呢?让我们先看看高中数学和初中数学有些什么样的转变吧。
一、高中数学的特点
1、 理论加强
2、 课程增多
3、 难度增大
4、 要求提高
二、掌握数学思想
高中数学从学习方法和思想方法上更接近于高等数学。学好它,需要我们从方法论的高度来掌握它。我们在研究数学问题时要经常运用唯物辩证的思想去解决数学问题。数学思想,实质上就是唯物辩证法在数学中的运用的反映。中学数学学习要重点掌握的的数学思想有以上几个:集合与对应思想,初步公理化思想,数形结合思想,运动思想,转化思想,变换思想。
例如,数列、一次函数、解析几何中的直线几个概念都可以用函数(特殊的对应)的概念来统一。又比如,数、方程、不等式、数列几个概念也都可以统一到函数概念。
再看看下面这个运用“矛盾”的观点来解题的例子。
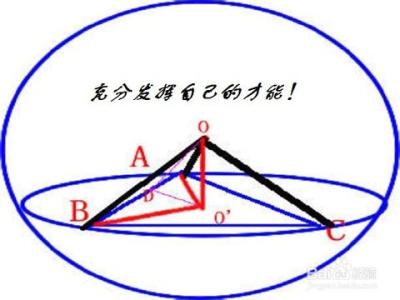
已知动点Q在圆x2+y2=1上移动,定点P(2,0),求线段PQ中点的轨迹。
分析此题,图中P、Q、M三点是互相制约的,而Q点的运动将带动M点的运动;主要矛盾是点Q的运动,而点Q的运动轨迹遵循方程x02+y02=1;次要矛盾关系:M是线段PQ的中点,可以用中点公式将M的坐标(x,y)用点Q的坐标表示出来。
x=(x0+2)/2
y=y0/2
显然,用代入的方法,消去题中的x0、y0就可以求得所求轨迹。
数学思想方法与解题技巧是不同的,在证明或求解中,运用归纳、演绎、换元等方法解题问题可以说是解题的技术性问题,而数学思想是解题时带有指导性的普遍思想方法。在解一道题时,从整体考虑,应如何着手,有什么途径?就是在数学思想方法的指导下的普遍性问题。
有了数学思想以后,还要掌握具体的方法,比如:换元、待定系数、数学归纳法、分析法、综合法、反证法等等。只有在解题思想的指导下,灵活地运用具体的解题方法才能真正地学好数学,仅仅掌握具体的操作方法,而没有从解题思想的角度考虑问题,往往难于使数学学习进入更高的层次,会为今后进入大学深造带来很有麻烦。
在具体的方法中,常用的有:观察与实验,联想与类比,比较与分类,分析与综合,归纳与演绎,一般与特殊,有限与无限,抽象与概括等。
要打赢一场战役,不可能只是勇猛冲杀、一不怕死二不怕苦就可以打赢的,必须制订好事关全局的战术和策略问题。解数学题时,也要注意解题思维策略问题,经常要思考:选择什么角度来进入,应遵循什么原则性的东西。一般地,在解题中所采取的总体思路,是带有原则性的思想方法,是一种宏观的指导,一般性的解决方案。
中学数学中经常用到的数学思维策略有:以简驭繁、数形结全、进退互用、化生为熟、正难则反、倒顺相还、动静转换、分合相辅。
如果有了正确的数学思想方法,采取了恰当的数学思维策略,又有了丰富的经验和扎实的基本功,一定可以学好高中数学。
三、学习方法的改进
身处应试教育的怪圈,每个教师和学生都不由自主地陷入“题海”之中,教师拍心某种题型没讲,高考时做不出,学生怕少做一道题,万一考了损失太惨重,在这样一种氛围中,往往忽视了学习方法的培养,每个学生都有自己的方法,但什么样的学习方法才是正确的方法呢?是不是一定要“博览群题”才能提高水平呢?
现实告诉我们,大胆改进学习方法,这是一个非常重大的问题。
(一) 学会听、读
我们每天在学校里都在听老师讲课,阅读课本或者资料,但我们听和读对不对呢?
让我们从听(听讲、课堂学习)和读(阅读课本和相关资料)两方面来谈谈吧。
学生学习的知识,往往是间接的知识,是抽象化、形式化的知识,这些知识是在前人探索和实践的基础上提炼出来的,一般不包含探索和思维的过程。因此必须听好老师讲课,集中注意力,积极思考问题。弄清讲得内容是什么?怎么分析?理由是什么?采用什么方法?还有什么疑问?只有这样,才可能对教学内容有所理解。
听讲的过程不是一个被动参预的过程,在听讲的前提下,还要展开来分析:这里用了什么思想方法,这样做的目的是什么?为什么老师就能想到最简捷的方法?这个题有没有更直接的方法?
“学而不思则罔,思而不学则殆”,在听讲的过程中一定要有积极的思考和参预,这样才能达到最高的学习效率。
阅读数学教材也是掌握数学知识的非常重要的方法。只有真正阅读和数学教材,才能较好地掌握数学语言,提高自学能力。一定要改变只做题不看书,把课本当成查公式的辞典的不良倾向。阅读课本,也要争取老师的指导。阅读当天的内容或一个单元一章的内容,都要通盘考虑,要有目标。
比如,学习反正弦函数,从知识上来讲,通过阅读,应弄请以下几个问题:
(1)是不是每个函数都有反函数,如果不是,在什么情况下函数有反函数?
(2)正弦函数在什么情况下有反函数?若有,其反函数如何表示?
(3)正弦函数的图象与反正弦函数的图象是什么关系?
(4)反正弦函数有什么性质?
(5)如何求反正弦函数的值?
(二) 学会思考
1、善于发现问题和提出问题
2、善于反思与反求
 爱华网
爱华网