高中数学函数的单调性也可以叫做函数的增减性。当函数f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。以下是小编为您整理的关于2017年高考数学函数的单调性必考知识点的相关资料,希望对您有所帮助。
高中数学知识点:函数的单调性
一般地,设函数f(x)的定义域为I:
如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1
如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1f(x2).那么就是f(x)在这个区间上是减函数。
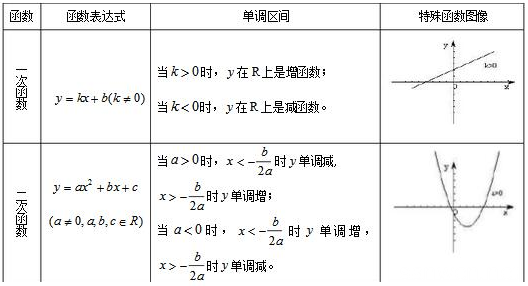
高中数学知识点:函数的单调区间
单调区间是指函数在某一区间内的函数值Y,随自变量X增大而增大(或减小)恒成立。如果函数y=f(x)在某个区间是增函数或减函数。那么就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间叫做y=f(x)的单调区间。
高中数学知识点:函数的单调图像
高中数学知识点:函数的单调性的应用
高中数学知识点:求函数单调性的基本方法
解:先要弄清概念和研究目的,因为函数本身是动态的,所以判断函数的单调性、奇偶性,还有研究函数切线的斜率、极值等等,都是为了更好地了解函数本身所采用的方法。其次就解题技巧而言,当然是立足于掌握课本上的例题,然后再找些典型例题做做就可以了,这部分知识仅就应付解题而言应该不是很难。最后找些考试试卷题目来解,针对考试会出的题型强化一下,所谓知己知彼百战不殆。 1、把握好函数单调性的定义。证明函数单调性一般(初学最好用定义)用定义(谨防循环论证),如果函数解析式异常复杂或者具有某种特殊形式,可以采用函数单调性定义的等价形式证明。另外还请注意函数单调性的定义是[充要命题]。
2、熟练掌握基本初等函数的单调性及其单调区间。理解并掌握判断复合函数单调性的方法:同增异减。
3、高三选修课本有导数及其应用,用导数求函数的单调区间一般是非常简便的。 还应注意函数单调性的应用,例如求极值、比较大小,还有和不等式有关的问题。
高中数学知识点:例题
判断函数的单调性y = 1/ x的平方-2x-3。
设x^2-2x-3=t,
令x^2-2x-3=0,
解得:x=3或x=-1,
当x>3和x<-1时,t>0,
当-1
所以得到x^2-2x-1对称轴是1。
根据反比例函数性质:
在整个定义域上是1/t是增函数。
当t>0时,x>3时,
t是增函数,1/t是减函数,
所以(3,+∞)是减区间,
而x<-1时,t是减函数,
所以1/t是增函数。
因此(-∞,-1)是增区间,
当x<0时,
-1
所以1/t是增函数,
因此(-1,1)是增区间,
而1
因此(1,3)是减区间,
得到增区间是(-∞,-1)和(-1,1),
(1,3)和(3,+∞)是减区间。
高中数学知识点:判断复合函数的单调性
方法:1、导数
2、构造基本初等函数(已知单调性的函数)
3、复合函数 4.定义法 5.数形结合 复合函数的单调性一般是看函数包含的两个函数的单调性
(1)如果两个都是增的,那么函数就是增函数
(2)一个是减一个是增,那就是减函数
(3)两个都是减,那就是增函数
高中数学知识点:复合函数求导公式
F'(g(x)) = [ F(g(x+dx)) - F(g(x)) ] / dx ......
(1) g(x+dx) - g(x) = g'(x)*dx = dg(x) ........
(2) g(x+dx) = g(x) + dg(x) .........
(3) F'(g(x)) = [ F(g(x) + dg(x)) - F(g(x)) ] /dx = [ F(g(x) + dg(x)) - F(g(x)) ] / dg(x) * dg(x)/dx = F'(g) * g'(x)
高三选修课本有导数及其应用把握好函数单调性的定义。证明函数单调性一般用定义法.函数的单调性就是随着x的变大,y在变大就是增函数,y变小就是减函数,具有这样的性质就说函数具有单调性。
 爱华网
爱华网