方差的计算、知识点归纳
方差在考试中考察不是很难,记住基本公式往里带就能解答正确,但是方差的概念让不少同学为此很是头痛。那方差到底是什么,怎样计算呢,下面小编就为大家整理一些题型和解题方法技巧。
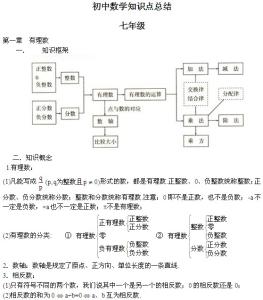
一、 概念和公式
方差的概念与计算公式,例1 两人的5次测验成绩如下:X: 50,100,100,60,50 E(X)=72;Y: 73, 70, 75,72,70 E(Y)=72。平均成绩相同,但X 不稳定,对平均值的偏离大。方差描述随机变量对于数学期望的偏离程度。单个偏离是消除符号影响方差即偏离平方的均值,记为D(X):直接计算公式分离散型和连续型,具体为:这里 是一个数。推导另一种计算公式得到:“方差等于平方的均值减去均值的平方”。其中,分别为离散型和连续型计算公式。 称为标准差或均方差,方差描述波动程度。

基本定义:设X是一个随机变量,若E{[X-E(X)]2}存在,则称E{[X-E(X)]2}为X的方差,记为D(X),Var(X)或DX。即D(X)=E{[X-E(X)]2}称为方差,而σ(X)=D(X)0.5(与X有相同的量纲)称为标准差(或均方差)。即用来衡量一组数据的离散程度的统计量。方差刻画了随机变量的取值对于其数学期望的离散程度。(标准差、方差越大,离散程度越大。否则,反之)若X的取值比较集中,则方差D(X)较小,若X的取值比较分散,则方差D(X)较大。因此,D(X)是刻画X取值分散程度的一个量,它是衡量取值分散程度的一个尺度。
当数据分布比较分散(即数据在平均数附近波动较大)时,各个数据与平均数的差的平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。因此方差越大,数据的波动越大;方差越小,数据的波动就越小
二、 计算方法和原理
若x1,x2,x3......xn的平均数为m则方差方差公式方差公式例1 两人的5次测验成绩如下:
X: 50,100,100,60,50 E(X )=72;
Y: 73, 70, 75,72,70 E(Y )=72。
平均成绩相同,但X 不稳定,对平均值的偏离大。方差描述随机变量对于数学期望的偏离程度。
单个偏离是消除符号影响方差即偏离平方的均值,记为D(X ):
直接计算公式分离散型和连续型,具体为:这里 是一个数。推导另一种计算公式
得到:“方差等于平方的均值减去均值的平方”。
其中,分别为离散型和连续型的计算公式。 称为标准差或均方差,方差描述波动。
设一组数据x1,x2,x3……xn中,各组数据与它们的平均数x(拔)的差的平方分别是(x1-x拔)2,(x2-x拔)2……(xn-x拔)2,那么我们用他们的平均数来衡量这组数据的波动大小,并把它叫做这组数据的方差。
方差分析的基本原理是认为不同处理组的均数间的差别基本来源有两个:
(1) 随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示, 记作SSw,组内自由度dfw。
(2) 实验条件,即不同的处理造成的差异,称为组间差异。用变量在各组的均值与总均值之偏差平方和表示,记作SSb,组间自由度dfb。
总偏差平方和 SSt = SSb + SSw。
组内SSw、组间SSb除以各自的自由度(组内dfw =n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MSw和MSb,一种情况是处理没有作用,即各组样本均来自同一总体,MSb/MSw≈1。另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体。那么,MSb>>MSw(远远大于)。
MSb/MSw比值构成F分布。用F值与其临界值比较,推断各样本是否来自相同的总体
三、 计算和性质
方差的计算公式D(X)=E(X²)-[E(X)]²
例题:随机变量X的分布函数F(X)=
 爱华网
爱华网