高中数学有许多奇妙之处,发人深省,高中数学的奇妙驱使人们不断深入研究数学。以下是小编为您整理的关于2017年高考数学直线与圆的位置关系的相关资料,希望对您有所帮助。
高中数学直线与圆的位置关系一
高中数学直线与圆的位置关系二
圆上一点的切线方程
如果在平面直角坐标系中还可以直接将
直线方程: 与圆的方程: 联立得出
若判别式>0 则该方程有两个根,即直线与圆有两个交点,相交;
若判别式=0 则该方程有一个根,即直线与圆有一个交点,相切;
若判别式<0 则该方程有零个根,即直线与圆有零个交点,相离。
高中数学直线与圆的位置关系判断
当△<0时,直线与圆没有公共点;
当△=0时,直线与圆相切;
当△>0时,直线与圆相交。
2.求出圆心到直线的距离d,半径为r
d>r,则直线与圆相离,反之相交
d=r,则直线与圆相切
直线与圆的位置关系例题分析
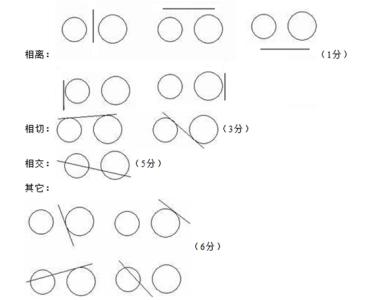
请你类比一条直线和一个圆的三种位置关系,在图,在①、②、③中,分别各画出一条直线,使它与两个圆都相离、都相切、都相交,并在图④中也画上一条直线,使它与两个圆具有不同于前面3种情况的位置关系
【考点】作图—复杂作图;圆与圆的位置关系
【分析】相离时,直线和任意一圆都没有交点;相切时,直线和每个圆都只有一个交点;相交时,直线和每个圆都有2个交点;可选和一个相离,一个相切或者其他。
【解答】解:答案不唯一,可供参考的有:
【点评】本题考查学生的动手能力以及分类概括能力:有都相离的;都相切的;都相交的,也有可能一个相交,一个相切。
 爱华网
爱华网