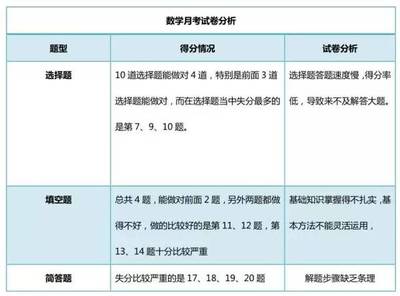
考试是检测学生学习效果的重要手段和方法,考前需要做好各方面的知识储备。下面是小编为大家整理的上海高考数学考点分析,希望对大家有所帮助!
上海高考数学考点分析
一、填空题:1. 不等式的运算;掌握集合的“交”、“并”、“补”等运算
2. 函数的有关概念,函数的最大值
3. 会根据已知三角比的值求角
4. 掌握指数函数的性质,掌握互为反函数的两个函数之间的关系
5. 复数的四则运算
6. 诱导公式,两角和与差的正弦、余弦、正切
7. 曲线与方程(双曲线标准方程和几何性质;抛物线标准方程和几何性质)
8. 随机事件与概率
9. 二项式定理
10. 数列的有关概念(等差数列,掌握等差数列的通项公式及前
项和公式;理解数列、数列的项、通项、有穷数列、无穷数列、递增数列、递减数列、常数列等概念)
11. 掌握参数方程与直角坐标方程的互化,加深对曲线方程的理解,强化数形结合观点,掌握圆与椭圆的参数方程
12. 会用球的表面积和体积公式进行有关的度量计算
13. 向量的度量计算
14. 数列的新定义(数列的有关概念:理解数列、数列的项、通项、有穷数列、无穷数列、递增数列、递减数列、常数列等概念)
二、选择题:15.圆的标准方程和一般方程;能在简单的问题情景中判断条件的充分性、必要性或充分必要性;空间直线与平面的位置关系
不等式的基本性质,会用不等式基本性质判断不等关系
16. 函数的基本性质,通过对函数零点的研究,体会“二分法”和逼近思想
17. 等差数列,掌握等差数列的通项公式及前
项和公式;等比数列,掌握等比数列的通项公式及前
项和公式;会(体验)用类比的思想方法对等差数列和等比数列进行研究(的活动)
18. 三角函数综合
三、解答题:19. 立体几何,会在简单的空间图形中用向量方法进行有关角(包括异面直线所成角)的度量计算,掌握棱锥的有关概念以及正棱锥的有关性质,会解决椎体的表面积、体积的计算问题
20.
21. 数列型应用题

22. 新定义函数题
 爱华网
爱华网