复数x被定义为二元有序实数对(a,b)[1] ,记为z=a+bi,这里a和b是实数,i是虚数单位。在复数a+bi中,a=Re(z)称为实部,b=Im(z)称为虚部。当虚部等于零时,这个复数可以视为实数;当z的虚部不等于零时,实部等于零时,常称z为纯虚数。复数域是实数域的代数闭包,也即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受。
复数的四则运算规定为:加法法则:(a+bi)+(c+di)=(a+c)+(b+d)i;减法法则:(a+bi)-(c+di)=(a-c)+(b-d)i;乘法法则:(a+bi)·(c+di)=(ac-bd)+(bc+ad)i;除法法则:(a+bi)÷(c+di)=[(ac+bd)/(c²+d²)]+[(bc-ad)/(c²+d²)]i.
例如:[(a+bi)+(c+di)]-[(a+c)+(b+d)i]=0,最终结果还是0,也就在数字中没有复数的存在。
[(a+bi)+(c+di)]-[(a+c)+(b+d)i]=Z是一个函数。
主要内容
定义
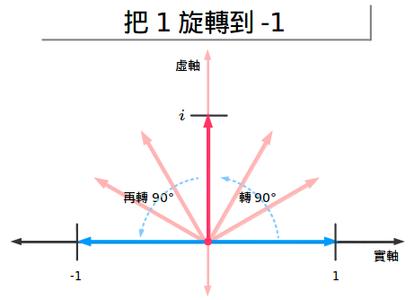
数集拓展到实数范围内,仍有些运算无法进行,(比如对负数开偶数次方),为了使方程有解,我们将数集再次扩充。
在实数域上定义二元有序对z=(a,b),并规定有序对之间有运算"+","x" (记z1=(a,b),z2=(c,d)):
z1 + z2=(a+c,b+d)
z1 x z2=(ac-bd,bc+ad)
容易验证,这样定义的有序对全体在有序对的加法和乘法下成一个域,并且对任何复数z,我们有
z=(a,b)=(a.0)+(0,1) x (b,0)
令f是从实数域到复数域的映射,f(a)=(a,0),则这个映射保持了实数域上的加法和乘法,因此实数域可以嵌入复数域中,可以视为复数域的子域。
记(0,1)=i,则根据我们定义的运算,(a,b)=(a.0)+(0,1) x (b,0):=a+bi,i x i=(0,1) x (0,1)=(-1,0)=-1,这就只通过实数解决了虚数单位i的存在问题。
形如 的数称为复数(complex number),其中规定i为虚数单位,且 (a,b是任意实数)
我们将复数 中的实数a称为复数z的实部(real part)记作Rez=a
实数b称为复数z的虚部(imaginary part)记作 Imz=b.
当a=0且b≠0时,z=bi,我们就将其称为纯虚数。
复数的模
将复数的实部与虚部的平方和的正的平方根的值称为该复数的模,记作∣z∣.
即对于复数 ,它的模
复数的集合用C表示,实数的集合用R表示,显然,R是C的真子集。
复数集是无序集,不能建立大小顺序。
 爱华网
爱华网



