四色猜想的书面常规证明
□秋屏
通常人们把四色猜想称之为世界近代三大数学难题之一(另外两个是费马大定理和哥德巴赫猜想),其内容是:“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”用数学语言表示,即“将平面任意地细分为不相重迭的区域,每一个区域总可以用‘1’、‘2’、‘3’、‘4’这四个数字之一来标记,而不会使相邻的两个区域得到相同的数字。”一百五十多年以来,世界各国的数学家们等,为之苦思冥想、绞尽脑汁欲将其证明为一个定理来。其间一些人宣称此猜想得以证明,但后来又被人推翻,直至1976年6月,美国数学家哈肯与阿佩尔称:他们在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿判断,终于完成了四色猜想成为定理的证明。此举轰动了世界,以致于当两位数学家将他们的研究成果发表的时候,当地的邮局在当天发出的所有邮件上都加盖了“四色足够”的特制邮戳,以庆祝这一难题获得解决。此后到最近几年前又有人称他们利用计算机进一步加以验证,以证实了证明的正确性。于是,目前大都认为这一百多年前的猜想,现已是个可以加以证明的“四色定理”了。最近两年我国公众人物黎鸣又突然宣称:他无需计算机,单凭他发现的“公理”再加上他的什么逻辑,就可用书面的常规的定理证明方法证明“四色定理”云云。于是便遭到方舟子等人的驳斥和批判,致使黎、方二人居然公开打赌而最终以决输赢。
如此一百五十多年间真可谓沸沸扬扬,好不热闹,为着这一猜想引出各路人马摆开一场场学术的鏖战。关于计算机的证明方式和过程是怎样进行并得到数学界认可的,我不太清楚,也不太关注。我所关注的是怎样用书面的常规方法加以证明,以使四色猜想成为定理,成为一如数学上其他定理采取书面传统的证明方法得证那样而让人容易接受认可的定理。近闻黎鸣先生的宣称,十分惊喜,于是悉心阅读思考,结果却发现他并没真正证明出来。黎鸣先生在证明过程中提出了破解“四色猜想”的两个基本公理,第一个为“公理一:凡处于球面或平面上的地图面积(国家、省、湖泊、海洋等),均与其相邻的面积(国家、省、湖泊、海洋等)处于三类不同的全相邻的关系之中,即全相邻数分别等于2、3、4的全相邻的关系之中。”并进一步解释道:
“关于这个公理,其实是前述的相邻几何学中‘黎鸣公理三角’中的第四行所指示的内容。这里稍作说明的是,为什么球面或平面地图面积的全相邻数不可能等于或大于5以上的自然数。这可以通过大量试错的过程来获得证明,并以此而作为归纳性的公理。对于球面或平面地图上的面积而言,这可以认为是不争的事实,因此,我们可以直接引用为不证自明的公理。但对于一般的人们来说,我们也不妨运用图论的方法作出如下简捷而直观的证明。
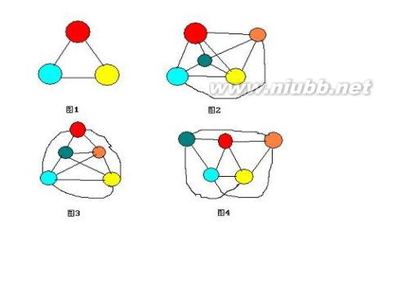
对于球面或平面上的一个全相邻数等于3的地图系统来说,如下面图1中所示的三角形,无论在这个三角形内还是外,为了保证所有色点之间的连线(表示相邻)不发生交叉(即不相邻),都最多只能增加一个色点(即最多只能使全相邻数增加到4),如果各增加两个以上色点的话,就将必然发生连线交叉的情况,而且三角形内外分别增加的这两个色点之间的连线,也显然不能不与原有的连线相互交叉,这可以分别参见图3、图4和图2。这就显然证明,在球面或平面的地图上,形成5个数字以上面积(色点)全相邻的关系是不可能的,于是关于全相邻数不可能等于和大于5以上数字的问题也同样即获得证明。”
黎鸣公理一图示如下:
其实,他的所谓公理一基本上就是四色猜想的等价表述,既说是不证自明的公理,又说可以通过大量试错的过程来获得证明,同时并说可运用图论的方法作出简捷而直观的证明,这本就存在着自相矛盾和逻辑混乱。同时大量试错而获得的结论,并不一定都是数学公理,定理能通过大量试错来证明其正确性,但它只是可通过书面常规证明证明出的定理,而非无法作推导证明且不正自明的公理。尤其需要指出的是,仅通过几例图示凭着直观而不加逻辑推演地画一画,从而就说命题的内容获证了,这也不是数学的证明方法和过程。试想若用如此没逻辑说服力的图论方法去证明命题,那么四色猜想谁都能证明,因为谁去画任何一张地图,只用不超过四种颜色就可使相邻国家不同色了的。即使用黎鸣先生的方法去证明四色猜想,而问题的关键就在于:为什么不存在“全相邻数不可能等于或大于5以上的自然数”呢?黎鸣先生根本没能令人信服地回答出,即根本没能从书面常规的方式证明出。所以他并没有发现什么新的公理,也根本没证明四色猜想的。他只不过是对该猜想作了并不高明的基本上的等价表述而已,他的宣称只会被稍加思考的人们加以彻底否定。而方舟子等人对其宣称只是作了想当然的肤浅的批判,却没能指出问题的实质所在。所以那些人鼓噪着的批判和嘲讽也是幼稚可笑的,丝毫没什么科学与社会意义。
那么四色猜想究竟该如何进行书面常规证明呢?笔者出于对科学的好奇和崇尚,于茶余饭后对此曾作了番苦心思考和探索,感谢真主,终于让我有所收获!兹谨将证明过程公之于众,敬请诸位方家明鉴,并祈不吝教正!
若要证明四色猜想首先得搞清楚这样一些概念、定义和性质,同时还必须先证明一些新定理。
区域和边界线的定义:同一平面内由线条所围构成的面积不为零的封闭几何图形,叫区域。围构成区域的线,叫该区域的边界线。
子区域的定义:一个区域内不包含有其他区域的基本区域,叫子区域。
母区域的定义:由子区域所组合成的复杂区域,叫母区域。
相邻和相邻边界线的定义:一个区域与另一区域存在共有的全部或部分边界线(是线,而不仅仅是点),则这两个区域叫相邻。共有的全部或部分边界线,叫相邻边界线。
被部分封闭的子区域和被完全封闭的子区域的定义和性质:一个子区域与若干子区域相邻,若这个子区域的边界线部分由相邻边界线构成,则该子区域叫被与之有相邻边界线的若干子区域部分封闭。被部分封闭的子区域在一定范围内将不再与部分封闭它的若干子区域以外的其他任何子区域相邻;一个子区域与若干子区域相邻,若这个子区域的边界线纯由相邻边界线构成,则该子区域叫被与之有相邻边界线的若干子区域完全封闭。被完全封闭的子区域在所有范围内将不再与完全封闭它的若干子区域以外的其他任何子区域相邻。
全相邻的定义和性质:同一平面内由若干子区域所组合成的母区域中,当其中任何一个子区域都与其余的子区域相邻,则这若干子区域叫全相邻。由于相邻时存在着部分封闭和完全封闭的情形,则相邻的子区域数目愈多,全相邻的可能性就会愈小。
相邻定理一:同一平面内只有四个子区域,要使它们在尽可能全相邻的条件下而尽可能不被完全封闭,当这四个子区域全相邻时,则其中就必会有某一个子区域被其余三个完全封闭。
相邻定理一图示(图中数字系子区域名称):
相邻定理一证明过程:
根据命题题设和相关定义作图可知,子区域(1)、(2)、(3)、(4)全相邻,子区域(1)、(2)、(4)分别不被相应的其余三个完全封闭。线段AB——在子区域(1)中按顺时针方向读,系子区域(1)和子区域(2)的相邻边界线;BC——在子区域(1)中按顺时针方向读,系子区域(1)和子区域(3)的相邻边界线;CD——在子区域(1)中按顺时针方向读,系子区域(1)和子区域(4)的相邻边界线;FB——在子区域(2)中按顺时针方向读,系子区域(2)和子区域(3)的相邻边界线;EF——在子区域(2)中按顺时针方向读,系子区域(2)和子区域(4)的相邻边界线;FC——在子区域(3)中按顺时针方向读,系子区域(3)和子区域(4)的相邻边界线。
那么子区域(3)为何必被其余三个完全封闭呢?假设区域(3)不被其余三个完全封闭,则其边界线就不纯由相邻边界线构成,即BC、FB、FC就不纯是相邻边界线。当BC不是相邻边界线时,子区域(1)和子区域(3)就不相邻,这与命题题设条件四个子区域全相邻矛盾,所以假设不能成立;当FB不是相邻边界线时,子区域(2)和子区域(3)就不相邻,这与命题题设条件四个子区域全相邻矛盾,所以假设不能成立;当FC不是相邻边界线时,子区域(3)和子区域(4)就不相邻,这与命题题设条件四个子区域全相邻矛盾,所以假设不能成立;当BC、FB同时都不是相邻边界线时,子区域(1)和子区域(3)就不相邻,子区域(2)和子区域(3)就不相邻,这与命题题设条件四个子区域全相邻矛盾,所以假设不能成立;当BC、FC同时都不是相邻边界线时,子区域(1)和子区域(3)就不相邻,子区域(3)和子区域(4)就不相邻,这与命题题设条件四个子区域全相邻矛盾,所以假设不能成立;当FB、FC同时都不是相邻边界线时,子区域(2)和子区域(3)就不相邻,子区域(3)和子区域(4)就不相邻,这与命题题设条件四个子区域全相邻矛盾,所以假设不能成立。如此以来,假设在所有情况下都不能成立,因此子区域(3)必被其余三个完全封闭,从而使得命题得证。
相邻定理二:同一平面内只有五个子区域,要使它们在尽可能全相邻的条件下而尽可能不被完全封闭,当其中有那样四个子区域全相邻时,则这四个中的某一个就必会被相应的其余三个完全封闭。被完全封闭的那个子区域,将不可能再与相应的余下的第五个子区域相邻。同时,另外的四个子区域全相邻时,则必有一个不可能与相应的余下的那第五个子区域,即上述的那个被完全封闭的子区域相邻。这样以来,这五个子区域中就会有两个不可能相邻,即五个子区域是不可能全相邻的,只可能存在每四个子区域全相邻。
相邻定理二图示(图中数字系子区域名称):
相邻定理二证明过程:
根据命题题设和相关定义作图可知,子区域(1)、(2)、(3)、(4)全相邻,子区域(1)、(2)、(4)、(5)全相邻。
当那样四个子区域,即子区域(1)、(2)、(3)、(4)全相邻时,子区域(3)是否必会被子区域(1)、(2)、(4)完全封闭呢?利用反证法等,即可证得子区域(3)必会被子区域(1)、(2)、(4)完全封闭,以及子区域(3)将不可能再与相应的余下的第五个子区域,即子区域(5)相邻。证明步骤过程与相邻定理一的证明步骤过程相类似,这里不再重复。
那么另外四个子区域,即子区域(1)、(2)、(4)、(5)全相邻时,由上述证明结论可知,子区域(5)不与子区域(3)相邻,所以子区域(1)、(2)、(4)、(5)这四个子区域中,就会有一个子区域,即子区域(5)不可能与相应的余下的那第五个子区域,即被完全封闭的子区域(3)相邻。
这样以来,子区域(1)、(2)、(3)、(4)、(5)这五个子区域中就会有两个不可能相邻,即五个子区域是不可能全相邻的,只可能存在每四个子区域全相邻。
由以上证明过程可知,命题得证。
相邻定理三:同一平面内有五个以上的子区域,要是它们尽可能全相邻,只可能存在每四个子区域可全相邻,而不可能存在每四个以上的子区域可全相邻。
相邻定理三证明过程:
当只有五个子区域时,由相邻定理二可知,只可能存在每四个子区域可全相邻,而不可能存在五个子区域可全相邻。所以子区域增加至五个以上时,鉴于全相邻的定义和性质所决定,也就只可能存在每四个子区域可全相邻,而不可能存在每四个以上的子区域可全相邻。
所以通过以上的直观推论,配合作图,命题即可得到证明。
相邻定理四:同一平面内对于任何一个母区域,不论子区域的数量是多少,只可能存在每两个、三个、四个子区域全相邻的状态。
相邻定理四证明过程:
当子区域有两个时,根据全相邻的定义可知,可形成两个子区域全相邻。当子区域有三个时,根据全相邻的定义可知,可形成三个子区域全相邻。当子区域有四个时,根据全相邻的定义可知,可形成四个子区域全相邻。当子区域有五个时,根据全相邻的定义和相邻定理二可知,可形成每四个子区域全相邻。当子区域有五个以上时,根据全相邻的定义和相邻定理三可知,可形成每四个子区域全相邻。
由以上分类推演可知,不论子区域的数量是多少,只可能存在每两个、三个、四个子区域全相邻的状态,因而命题得证。
若给每两个全相邻的子区域组成的母区域着色,使相邻子区域颜色不同,至少需用两种或三种色种;若给每三个全相邻的子区域组成的母区域着色,使相邻子区域颜色不同,至少需用三种或四种色种;若给每四个全相邻的子区域组成的母区域着色,使相邻子区域颜色不同,至少需用四种色种。所以根据相邻定理四可知,若将任何一个母区域中的每个子区域都着上颜色,要是相邻子区域的颜色不相同,最多选用四种色种就完全可以完成了,因而四色猜想得证。
2008年1月27日雪暮回历1429年1月18日起草于抱真轩灯下
2008年7月5日17时34分回历1429年7月1日于抱真轩脱稿
2008年11月11日0时36分回历1429年11月12日于抱真轩修改
(拙作并发表于《人民网》、《新华网》、《中国数学在线》、《西陆网·世界科学苑》、《数学中国》等媒体。)
【博主声明:我最后的结论仅仅是在描述那些现象而没能给出证明,等于还是没有证出。其实即使彻底证明了“只可能存在最多四个子区域全相邻”,也证明不了四色猜想的,因为“只可能存在最多四个子区域全相邻”,并不是“最多着四种颜色”的充要条件啊!这是因为:若给每三个全相邻的子区域组成的母区域着色,使相邻子区域颜色不同,至少需用三种或四种色种。同时,就我目前所阅读到的有关四色猜想的文章来看,谁也没证明出来。所以我倒觉得四色猜想应当是个无法证明的公理。另外,我仅认为自己最先并彻底证明了“西西弗斯串(数学黑洞)”这一数学之谜,谁若感兴趣可前去看看,很简单的,易于理解。另外,拙文《数学中的致命错误——反证法》,我觉得很值得探讨,截止目前,国际数学界还没一个人能驳倒我的论证,谁觉得有价值的话,尚请垂赐高论!】
 爱华网
爱华网