看过这样一道题,问,“程序结构化设计的三种基础结构,顺序、选择、循环是不是必须的?”当然,你知道这样一个论断,只要有这三种就足够了;但是能不能更少呢?答案是“可以”,原因就是递归能取代循环的作用,例如下面的对一个数组里面元素求和的函数:
float rsum (float a[], const int n)
{
if (n <= 0) return 0;
else return rsum(a, n ? 1) + a[n ? 1];
}
实际上就是:
sum = 0;
for (int i = 0; i < n; i++) sum += a[i];
但实际的情况是,任何的一种语言里面都有循环结构,但不是任何的语言都支持递归;套用一句话,递归是万能的,但没有递归不是万万不能的。然而,我看到现在的某些人,不管什么问题都要递归,明明循环是第一个想到的方法,偏偏费尽脑筋去寻找递归算法。对此,我真的不知道该说什么。
递归是算法吗
经常的看到“递归算法”、“非递归算法”,这种提法没有语义上的问题,并且我自己也这样用??递归的算法。但这也正说明了,递归不是算法,他是一种思想,正是因为某个算法的指导思想是递归的,所以才被称为递归算法;而一个有递归算法的问题,当你不使用递归作为指导思想,这样得到的算法就是非递归算法。??而对于循环能处理的问题,都有递归解法,在这个意义上说,循环算法都可以称为非递归算法。
我在这咬文嚼字没什么别的意思,只是想让大家知道,能写出什么样的算法,关键是看你编写算法时的指导思想。如果一开始就想到了循环、迭代的方法,你再费心耗神去找什么递归算法??即使找到了一种看似“简洁”的算法,由于他的低效实际上还是废物??你还在做这种无用功干什么?典型的学究陋习。如果你仅仅想到了递归的方法,现在你想用栈来消解掉递归,你做的工作仅仅是把系统做的事自己做了,你又能把效率提高多少?盲目的迷信消解递归就一定能提高效率是无根据的??你做的工作的方法如果不得当的话,甚至还不如系统原来的做法。
从学排列组合那天开始,我所知道的阶乘就是这个样子n! =1×2×……n。如果让我来写阶乘的算法,我也只会想到从1乘到n。再如,斐波那契数列,如果有人用自然语言描述的话,一定是这样的,开始两项是0、1,以后的每项都是前面两项的和。所以让我写也只会得到“保存前两项,然后相加得到结果”的迭代解法。??现在只要是讲到递归几乎就有他们的登场,美其名曰:“定义是递归的,所以我们写递归算法”。我想问的是,定义的递归抽象是从哪里来的?显然阶乘的定义是从一个循环过程抽象来的,斐波那契数列的定义是个迭代的抽象。于是,我们先从一个本不是递归的事实抽象出一个递归的定义,然后我们说,“因为问题的定义是递归的,因此我们很容易写出递归算法”,接着说,“我们也能将这个递归算法转化为循环、迭代算法”,给人的感觉就像是1÷3=0.33……,0.33……×3=0.99……,然后我们花了好大的心智才明白1=0.99……。
还是有那么些人乐此不疲,是凡讲到递归就要提到这两个,结果,没有一个学生看到阶乘那样定义没有疑问的,没有一个对于那个递归的阶乘函数抱有钦佩之情的??瞎折腾什么呢?所以,如果要讲递归,就要一个令人信服的例子,而这个例子非汉诺塔莫属。
汉诺塔的非递归解法
似乎这个问题的最佳解法就是递归,如果你想用栈来消解掉递归达到形式上的消除递归,你还是在使用递归的思想,因此,他本质上还是一个递归的算法。
我们这本黄皮书在谈论到“什么情况使用递归”的时候,在“3.问题的解法是递归的”这里面,就这样说了“有些问题只能用递归的方法来解决,一个典型的例子就是汉诺塔”。
但我坚信,如果一个问题能用分析的办法解决??递归实际上就是一个分析解法,能将问题分解成-1规模的同等问题和移动一个盘子,如果这样分解下去一定会有解,最后分解到移动1号盘子,问题就解决了??那么我也应该能用综合的办法解决,就是从当前的状态来确定怎样移动,而不是逆推得到决定。这是对实际工作过程的一个模拟,试想如果让我们去搬盘子,我们肯定不会用递归来思考现在应该怎么搬??只要8个盘子,我们脑子里的“工作栈”恐怕就要溢出了??我们要立即决定怎么搬,而不是从多少步之后的情景来知道怎么搬。下面我们通过模拟人的正向思维来寻找这个解法。
假设如下搬7个盘子的初始状态(选用7个是因为我曾经写出了一个1~6结果正确的算法,而在7个的时候才发现一个条件的选择错误,具体大家自己尝试吧),我们唯一的选择就是搬动1号盘子,但是我们的问题是向B搬还是向C搬?
显然,我们必须将7号盘子搬到C,在这之前要把6号搬到B,5号就要搬到C,……以此类推,就会得出结论(规律1):当前柱最上面的盘子的目标柱应该是,从当前柱上“需要搬动的盘子”最下面一个的目标柱,向上交替交换目标柱到它时的目标柱。就是说,如果当前柱是A,需要移动m个盘子,从上面向下数的第m个盘子的目标柱是C,那么最上面的盘子的目标柱就是这样:if(m % 2) 目标和第m个盘子的目标相同(C);else目标和第m个盘子的目标不同(B)。接下来,我们需要考虑如果发生了阻塞,该怎么办,如下所示:
3号盘子的目标柱是C,但是已经有了1号盘子,我们最直觉的反映就是??将碍事的盘子搬到另一根柱子上面去。于是,我们要做的是(规律2):保存当前柱的信息(柱子号、应该搬动的最下面一块盘子的号,和它的目标柱),以备当障碍清除后回到现在的柱子继续搬,将当前柱转换为碍事的盘子所在的柱子。假设这样若干步后,我们将7号盘子从A搬到了C,此时,保存当前柱号的栈一定是空了,我们该怎么办呢?
显而易见的,转换当前柱为B,把6号盘子搬到C。由此可得出(规律3):假设当前的问题规模为n,搬动第n个盘子到C后,问题规模减1,当前柱转换到另一个柱子,最下面的盘子的目标柱为C。
综上,我们已经把这个问题解决了,可以看出,关键是如何确定当前柱需要移动多少盘子,这个问题请大家自己考虑,给出如下例程,因为没有经过任何优化,本人的编码水平又比较低,所以这个函数很慢??比递归的还慢10倍。
#include
#include
using namespace std;
class Needle
{
public:
Needle() { a.push_back(100); }//每一个柱子都有一个底座
void push(int n) { a.push_back(n); }
int top() { return a.back(); }
int pop() { int n = a.back(); a.pop_back(); return n; }
int movenum(int n) { int i = 1;while (a[i] > n) i++; returna.size() - i; }
int size() { return a.size(); }
int operator [] (int n) { return a[n]; }
private:
vector a;
};
void Hanoi(int n)
{
Needle needle[3],ns;//3个柱子,ns是转换柱子时的保存栈,借用了Needle的栈结构
int source = 0, target, target_m = 2, disk, m = n;
for (int i = n; i > 0; i--)needle[0].push(i);//在A柱上放n个盘子
while (n)//问题规模为n,开始搬动
{
if (!m) { source = ns.pop(); target_m = ns.pop();
m = needle[source].movenum(ns.pop());}//障碍盘子搬走后,回到原来的当前柱
if (m % 2) target = target_m; else target = 3 - source -target_m;//规律1的实现
if (needle[source].top() <needle[target].top())//当前柱顶端盘子可以搬动时,移动盘子
{
disk = needle[source].top();m--;
cout << disk << " move " << (char)(source + 0x41)<< " to "<< (char)(target + 0x41) <<endl;//显示搬动过程
needle[target].push(needle[source].pop());//在目标柱上面放盘子
if (disk == n) { source = 1 - source; target_m = 2; m = --n;}规律3的实现
}
else//规律2的实现
{
ns.push(needle[source][needle[source].size() - m]);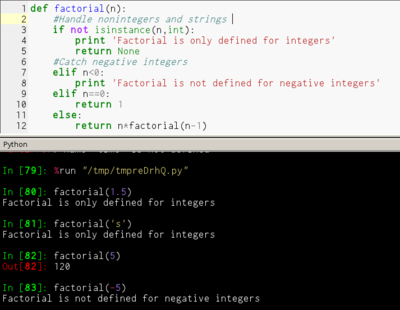
ns.push(target_m); ns.push(source);
m = needle[target].movenum(needle[source].top());
target_m = 3 - source - target; source = target;
}
}
}
这个算法实现比递归算法复杂了很多(递归算法在网上、书上随便都可以找到),而且还慢很多,似乎是多余的,然而,这是有现实意义的。我不知道现在还在搬64个盘子的僧人是怎么搬的,不过我猜想一定不是先递归到1个盘子,然后再搬??等递归出来,估计胡子一打把了(能不能在人世还两说)。我们一定是马上决定下一步怎么搬,就如我上面写的那样,这才是人的正常思维,而用递归来思考,想出来怎么搬的时候,黄瓜菜都凉了。正像我们做事的方法,虽然我今生今世完不成这项事业,但我一定要为后人完成我能完成的,而不是在那空想后人应该怎么完成??如果达不到最终的结果,那也一定保证向正确的方向前进,而不是呆在原地空想。
由此看出,计算机编程实际上和正常的做事步骤的差距还是很大的??我们的做事步骤如果直接用计算机来实现的话,其实并不能最优,原因就是,实际中的相关性在计算机中可能并不存在??比如人脑的逆推深度是有限的,而计算机要比人脑深很多,论记忆的准确性,计算机要比人脑强很多。这也导致了一个普通的程序员和一个资深的程序员写的算法的速度常常有天壤之别。因为,后者知道计算机喜欢怎么思考。
 爱华网
爱华网
