适合中国的货币乘数模型
作者:刘植荣
不久前,一家金融机构高管撰文称“货币乘数与存款准备金率成反比”,这样表述并不正确。存款准备金率的倒数是简单存款乘数,它是基础货币所能创造货币的倍数的最大值,它帮助初学者理解货币创造过程,但不能被用作现实货币政策分析,因为简单存款乘数的一个假设就是银行系统外没有现金流通,而事实上,银行系统外到处是钞票。所以说,货币乘数一定小于存款准备金率的倒数。
央行要求银行把吸收的存款向央行交存一定比率的法定准备金,用R表示,法定存款准备金率用r表示。除此之外,银行本身也要留存一定比率的超额准备金(excessreserve),以随时支付储户提款。我们把超额准备金用E表示,超额准备金率用e表示。
再有,企业从银行借款后,一般要提出一部分现金,用以支付员工的工资和日常开销。这样,银行系统之外必然要流通一些现金。中国央行把货币划分为三个层次,银行系统之外流通的现金叫M0,M0加上单位活期存款叫狭义货币M1,M1加上单位定期存款、个人存款和其他存款叫广义货币M2。为了便于下文的公式推导,我们把M0用C表示,把M2用M表示,把银行存款用D表示。由于中国的活期存款与定期存款的法定准备金率实行单一比率,故本文把现金比率(currency-depositratio)定义为银行系统之外的现金与银行各项存款总额的比率,我们用c表示。在此,请读者格外注意:教科书把现金比率定义为银行系统之外的现金与银行活期存款的比率。
在货币创造过程中,央行的法定存款准备金率只是其中的一个变量,超额准备金率以及现金比率也影响着货币创造。
假如一家银行把从央行获得的100元的货币投放贷给A企业,并假定r=10%,e=2%,c=6%。因为C+D=100,C/D=6%,从而得出C=(6÷106)×100=5.66元,即A企业从这100元借款中提取5.66元的现金,把剩下的100-5.66=94.34元存入银行账户。银行收到这笔存款后,要交存央行94.34×10%=9.43元法定存款准备金,自己留存94.34×2%=1.89元超额准备金,剩余的94.34-9.43-1.89=83.02元可供继续放贷。
B企业从银行借到这83.02元,提取C=(6÷106)×83.02=4.70元现金,把剩下的78.32元存入银行账户。银行收到这笔存款后,交存央行78.32×10%=7.83元法定存款准备金,自己留存78.32×2%=1.57元超额准备金,剩余的78.32-7.83-1.57=68.92元可供继续放贷。如此这般,周而复始。
观察以上数据可知,央行向银行投放的100元货币,银行每放贷一次,放贷金额、企业提取的现金、法定存款准备金和超额准备金均为上一次的83.02%,从而形成无穷递减等比数列,公比q=0.8302。根据无穷递减等比数列的求和公式S=a/(1-q),我们求出流出银行系统的现金总额C=5.66÷(1-0.8302)=33.33元,存款总额D=94.34÷(1-0.8302)=555.59元,法定存款准备金总额R=9.43÷(1-0.8302)=55.54元,超额准备金总额E=1.89÷(1-0.8302)=11.13元。货币总量M=C+D=33.33+555.59=588.92元。
我们知道,基础货币为银行系统外的现金与法定存款准备金和超额准备金之和,用B表示,则B=C+R+E=33.33+55.54+11.13=100元,正好是央行投放的100元基础货币。
货币乘数(moneymultiplier)就是货币总量与基础货币的比值,用m表示,则m=M/B。本例的货币乘数m=588.92÷100=5.89,而本例的简单存款乘数为10,两者相差甚远。
依据以上分析,我们就可把货币乘数公式推导出来。经济学上所讲的货币如不特别说明均指广义货币;同理,如不特别说明,货币乘数均指广义货币乘数。
因为B=C+R+E,而R=D×r,E=D×e,所以B=C+D×r+D×e。还因为c=C/D,所以C=D×c。综合前面方程得出B=D×c+D×r+D×e=D×(c+r+e)。又因为M=C+D=D×c+D=D×(c+1),所以,货币乘数m=M/B=D×(c+1)/﹝D×(c+r+e)﹞,化简并整理这个方程得m=(1+c)/(r+e+c)。这就是货币乘数模型。
现在,我们用这个货币乘数模型计算本文例子中的货币乘数m=(1+0.06)÷(0.1+0.02+0.06)=5.89,与用数列求和法计算的结果相同。
根据中国央行发布的2013年3月末货币数据,M=1035858.37亿元,B=253649.82亿元(央行叫“储备货币”),r=18.25%,e=2.0%,C=55460.52亿元,D=980397.86亿元。我们可计算出c=C/D=55460.52亿÷980397.86亿=5.66%。把r、e和c的值代入货币乘数模型,m=(1+0.0566)÷(0.1825+0.02+0.0566)=4.08。我们用m=M/B进行验算,m=1035858.37亿÷253649.82亿=4.08。
同样,我们用货币乘数模型计算出2012年第4季度末、第3季度末、第2季度末和第1季度末的货币乘数分别是3.85、4.02、4.07和3.95,而这4个季度的实际货币乘数分别是3.86、4.00、4.06和3.95。这证明,货币乘数模型m=(1+c)/(r+e+c)适用中国货币统计口径,其精确度远远高于乔顿货币乘数模型。
货币乘数模型是研究货币经济的一个非常重要的工具,通过它可以知道央行投放一定量的基础货币会创造出多少货币来;货币乘数模型也解释了货币总量是法定存款准备金率、超额准备金率和现金比率的函数,即使央行不对基础货币进行操作,调整这三个变量就可以控制货币总量。(本文发《新金融观察》2013年7月1日第09版)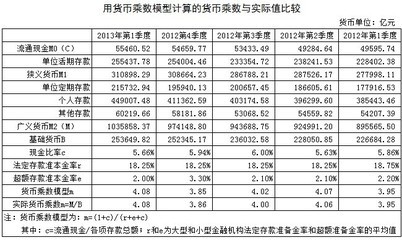
 爱华网
爱华网



