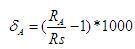前面在“求连续自然数立方和的公式”一文中，介绍了用列表法推导公式的过程。这种方法浅显易懂，的确有它的优越性。在“有趣的图形数”中，也曾经用图形法推出过求连续自然数平方和的公式：
这里用列表法再来推导一下这个公式，进一步体会列表法的优点。
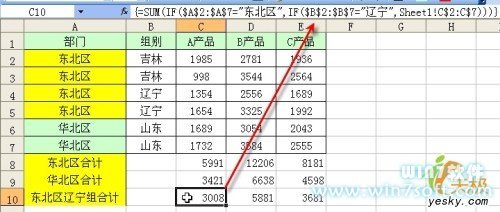
首先，算出从1开始的一些连续自然数的和与平方和，列出下表：
然后，以连续自然数的平方和为分子，连续自然数的和为分母，构成分数
用数学归纳法很容易证明等式的正确性，这样就轻而易举地推出了求连续自然数平方和的公式。
这个妙不可言的推导过程是数学家波利亚的杰作，关键之处是他运用了“猜想—证明”的思路。联想到当年著名文学家胡适也曾经有过“大胆假设，小心求证”的名言。看来，无论数学也好，文学也好，追求真理的道路是相通的。
这件事对我们教师有什么启示吗？有的，那就是：切莫轻视了对学生观察、类比和猜想能力的培养！这往往是培育创新思维的有效途径。
经常和Execl打交道的人肯定觉得求和公式是大家时常用到的。Excel里有哪几路求和公式呢？他们的使用方式又是怎样？我为大家汇总一下。Excel各种条件求和的公式汇总——步骤/方法Excel各种条件求和的公式汇总 1、使用SUMIF（）公式的单条件
混源天然气碳同位素计算公式推导：文献中（如Jenden et al.,1993；高先志, 1997），混源天然气碳同位素计算一般用近似计算，但是并没给出具体的推导过程。特别的，高先志（1997）基于“质量守恒原则,两种不同碳同位素浓度的甲烷混合，混合前后甲烷碳同
求数组长度的方法有两种 第一种是intarray[n];strlen(array);//这个方法可以求得字符串数组的长度char sizeof(array);sizeof（array）;//可以求的数组的长度
求专门讲方言的电视剧 比如重庆 上海 苏州 （东北的不要 多介绍几个我来帮他解答图片符号编号排版地图
以动画演示单项式乘以多项式的公式推导1.（方案一）新建画板，用文字工具输入教材例题：为了扩大绿地的面积，要把街心花园的一块长m米，宽b米的长方形绿地，向两边分别加宽a米和c米，你能用几种方法表示扩大后绿地的面积？2.单击工具栏下方“自定义工
爱华网