Herzer认为,对于大晶粒的无规取向多晶态材料,每个晶粒的磁化强度按各个晶粒的易磁化方向排列,在每个晶粒中形成磁畴,材料的磁化过程由每个晶粒的磁晶各向异性能决定。但是,对于无规取向的细小多晶材料来说,各个微小的晶粒中的原子磁矩同时受到铁磁交换作用以及磁晶各向异性场的作用,它们的磁化不再能够像大晶粒那样按照每个晶粒的易磁化方向排列。
定义一个与交换作用相关的特征长度Lex(Ferromegnetic exchangelength),称之为铁磁交换长度,它由交换能和磁晶各向异性能决定。当材料的晶粒尺寸D,其表示式如下:
=K1/N1/2;N=(Lex/D)3;Lex=[A/]1/2
上式中,A为交换作用劲度(亦称为交换积分),N未铁磁交换长度范围内的晶粒个数。得:
=K14D6/A3
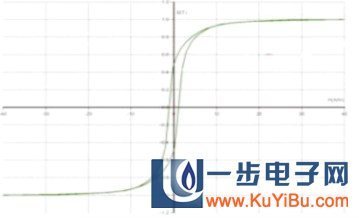
对于α-Fe(Si) , A=10-11J/m、K1=8KJ/m3,由此,可以计算与D的关系。
图纳米晶中与D的关系
由此可见,随着D的减小,平均涨落减小,当D=10~20nm时,趋近于零,磁晶各向异性被有效平均掉了。
若假定磁化过程是自旋的一致转动过程,则矫顽力和仅与起始磁导率有关,从而导出以下公式:
Hc=Pc/Js=PcK14D6/(JsA3)
μi=Pμ/[u0]=PuJs2A3/u0K14D6
式中,Pc和Pμ为常数,Js为饱和磁化强度。以上式子说明,若合金的晶粒尺寸D
这一结果表明,随着晶粒尺寸的变小,磁导率显著上升,矫顽力明显下降,除此之外,上述结果还表明,纳米晶软磁材料的磁性能和有效磁晶各向异性能有关,选择合适的处理方法及其处理条件,使有效磁晶各向异性能达到极小值,是获得高磁导率的条件之一。当D>Lex时,这一情况和通常的较大晶粒软磁材料完全不同,此时晶粒的大小远远超过畴壁厚度,磁化过程取决于晶界上的畴壁钉扎,因此,Hc∝D-1,1/μi∝D-1,即随晶粒尺寸的减小,磁导率下降而矫顽力上升。
纳米晶软磁材料具有优异软磁性能的另一个原因是其具有较低的饱和磁致伸缩系数。Herzer认为,纳米晶合金材料的饱和磁致伸缩系数是结晶相和剩余非晶相磁致伸缩的平均:
λs=λsa(1+Vc)+λscVc
其中,Vc是结晶相的体积百分含量,λsa和λsc分别是结晶相和剩余非晶相的饱和磁致伸缩系数。
已知α-Fe(Si)的饱和磁致伸缩系数与Si的含量有关,当Si的原子百分含量约为11.3%时,其饱和磁致伸缩系数为零,Si的含量增加时,饱和磁致伸缩系数为负数。在此,我们估计其饱和磁致伸缩系数为4×10-6,非晶相的饱和磁致伸缩系数可以使用原始试样的数据,即36×10-6左右。
为了获得非晶态合金的最佳软磁性能,除了要求较低的有效磁晶各向异性场和饱和磁致伸缩系数外,还要满足一个新的条件,即晶化相的饱和磁化强度和剩余非晶相的磁化强度之差△Ms=Msc-Msa为最小,因为较大的差值将造成合金的不均匀化,在晶相和非晶相的界面形成较强的杂散场而妨碍畴壁位移。
 爱华网
爱华网



