毕业设计：卷积码编码及其解码的程序设计_之＆凡

1绪论

信息论作为现代科学技术中具有重大意义的崭新学科的诞生标志是美国数学家香农1948年发表的著名论述《通信的数学理论》，至此以后编码技术已发展了半个多世纪，编码理论起源于现代通信技术与电子计算机技术中差错控制研究的需要，是信息论的一个专门分支。

1．1编码理论的基本概念

信息论源于对通信系统的研究，又服务于通信系统。Shannon给出的通信系统模型如图1-1所示。信息传输或通信的目的是把收方不知道的信息及时、可靠、完整、安全而又经济地传送给指定的收方。

图1-1 通信系统的基本模型

信源是产生消息和消息序列的源，它是事物各种运动状态或存在的集合。信源发出的消息有语音、图像、文字等，人的大脑思维活动也是一种信源。信源的输出是消息，消息是具体的，但它不是信息本身。编码器可分信源编码器、信道编码器、保密编码器三种。信源编码是对信源输出的消息进行适当的变换和处理，把信息变换成信号，目的是为了提高信息传输的效率，是传输更为经济、有效，还要去掉一些与被传信息无关的多余度；信道编码是为了提高信息传输的可靠性而对消息进行的变换和处理；保密编码是为了保证信息的安全性。信道是指通信系统把载荷消息的信号从甲地传输到乙地的媒介。信道除了传送信号以外，还有存储信号的作用。译码器就是把编码器输出的编码信号进行反变换。一般认为这种变换是可逆的。译码器也可分为信源译码器和信道译码器及保密译码器三种。信宿是消息传送的对象，即接收消息的人或机器。图1-1给出的模型只适用于收发两端单向通信的情况。它只有一个信源和一个信宿，信息传输也是单向的。更一般的情况是：信源和信宿各有若干个，即信道有多个输入和多个输出，另外信息传输也可以双向进行，例如广播通信是一个输入、多个输出的单向传输的通信，而卫星通信则是多个输入、多个输出的多向传输的通信。

1．2编码理论的发展历程

1948年，香农在《通信的数学理论》的论文中，用概率测度和数理统计的方法系统地讨论了通信的基本问题，香农理论的核心是：在通过系统中采用适当的编码后能够实现高效率和高可靠性的信息传输，并得出了信源编码定理和信道编码定理。这些定理给出了编码的性能极限，在理论上阐明了通信系统中的各种因素的相互关系，为人们寻找最佳通信系统提供了重要的理论依据。

1948年，香农在论文中提出并给出了简单的编码方法（香农编码）；

1952年，费诺（Fano）提出了一种费诺码；

1952年，霍夫曼（D.A.Huffman）构造了一种霍夫曼编码方法，并证明了它是最佳码。霍夫曼码是有限长度的块码中的最好的码，亦即代码总长度最短的码；

1956年，麦克米伦（B.McMillan）首先证明了惟一可译变长码的克拉夫特（Kraft）不等式；

1968年前后，埃利斯（P.Elias）发展了香农-费诺码，提出了算术编码的初步思路。而里斯桑内在1976年给出和发展了算术编码，1982他和兰登（G.G.Landon）一起将算术编码系统化，并省去了乘法运算，使其更为简化、易于实现；

1977年，由齐弗（J.Ziv）和兰佩尔（A.Lempel）提出了LZ算法，它是适用于通用信源的编码算法之一。1978年他们俩又提出了改进算法，而且齐弗也证明此方法可达到信源的熵值；

1990年，贝尔（T.C.Bell）等在LZ算法基础上又做了一系列变化和改进，现在LZ码已广泛应用于文本的数据压缩中。

1．3信息论研究的中心问题和发展

1.3.1 Shannon信息论的基本任务

1948年shannon发表了“通信的数学理论”奠定了信息论理论基础

基本任务是设计有效而可靠的通信系统：可靠是要使信源发出的消息经过传输后，尽可能准确地、不失真地再现在接收端；有效是用尽可能短的时间和尽可能少的设备来传输一定量的消息。

1.3.2 信息论的研究内容

狭义信息论（经典信息论）：研究信息测度，信道容量以及信源和信道编码理论。

一般信息论：研究信息传输和处理问题，除经典信息论外还包括噪声理论，信号滤波和预测，统计检测和估值理论，调制理论，信息处理理论和保密理论。

广义信息论：除上述内容外，还包括自然和社会领域有关信息的内容，如模式识别，计算机翻译，心理学，遗传学，神经生理学。

1.3.3 狭义信息论体系结构

至调制器的已编码序列

1.3.4 信息论发展简史

电磁理论和电子学理论对通信理论技术发展起重要的促进作用

1820－1830年，法拉第发现电磁感应；

莫尔斯1832－1835建立电报系统。1876年Bell发明电话；

1864麦克斯韦预言电磁波存在，1888年赫兹验证该理论；

1895年马可尼发明了无线电通信；

微波电子管导致微波通信系统，微波雷达系统；

激光技术使通信进入光通信时代；

1832年莫尔斯电码对shannon编码理论的启发；

1885年凯尔文研究了一条电缆的极限传信速率；

1922年卡逊对调幅信号的频谱结构进行研究；

1924年奈奎斯特证明了信号传输速率和带宽成正比；

1928年Hartley提出信息量定义为可能消息量的对数；

1939年Dudley发明声码器；

1940维纳将随机过程和数理统计引入通信与控制系统；

2卷积码编码

根据信息论的各种编码定理和通信系统的性能指标，编码问题可分解为信源编码，信道编码和密码编码三类。此次毕业设计是针对的是信道编码中的卷积码进行讨论的，所以首先将对信道编码给予介绍，之后再具体介绍卷积码。

2.1 信道编码简介

2.1.1 信道编码基本概念

信道编码的目的是为了改善通信系统的传输质量，由于实际信道存在着噪声和干扰，使发送的码字与信道传输后的码字之间存在着差异，即差错。信道编码的目的是为了改善通信系统的传输质量。由于实际信道中存在着噪声和干扰，使发送端和接收端的码字之间存在着差异，即差错，为了使由信源编码器输出的码字具有抗击信道中噪声干扰的能力，信道编码器要对信源编码器输出的码字进行变换，其原理是根据一定的规律在待发送的信息码中加入一些多余的码字（即校验元或监督元），以使受损和出错的信息仍能在接收端恢复，保证了传输的可靠性。即信道编码的主要任务就是够造出以最小的余度代价换取最大抗干扰性能的“好码”。

信道编码的实质是在信息码中增加一定数量的多余码元(称为监督码元)，使它们满足一定的约束关系，这样，由信息码元和监督码元共同组成一个由信道传输的码字。一旦传输过程中发生错误，则信息码元和监督码元间的约束关系被破坏。在接收端按照既定的规则校验这种约束关系，从而达到发现和纠正错误的目的。

信道编码按照对信息码元处理方法的不同可分为分组码和卷积码。所谓分组码就是将k个信息码元划分为一组，然后由k个码元按照一定规则产生r个监督码元，组成长度为n=k+r的码组，监督码元仅限于监督本码组中的信息码元，分组码用符号表示为（n,k），并规定前面k位为信息位，后面r位为监督位。而卷积码也是将k个信息码元划分为一组，而与分组码的不同就是在于其r个监督码元的产生不但与本码组的信息码元有关，而且还与前面若干个信息码元有关，即不是分组监督，而是每个监督码元对它的前后码元都实行监督，前后相连，卷积码也因此称为连环码，卷积码用符号表示为（n,k,m）,n输出的编码码组的码元个数，其中k表示信息位的个数，而m表示编码器中所含移位寄存器的个数，卷积码中编码后的n个码元不仅与当前段的k个信息有关，而且也与前面m段的信息有关，编码过程中相互关联分组数为m+1,L =m+1被称为此码的约束度，而其相互关联的码元为nL个，nL通常被称为这种码的约束长度。卷积码的纠错能力随着N的增加而增大，在编码器复杂程度相同的情况下，卷段积码的性能优于分组码。

2.1.2 信道编码的分类

信道FEC编码的分类方式很多，彼此之间又互相涵盖。常见的分类方式有：

(1) 根据监督码元与信息组之间的关系，可以分为分组码和卷积码两大类。若本

组的监督码元仅与本码组的信息码元有关，而与其它码组的信息码元无关，则称这类码为分组码。若本码组的监督码元不仅和本码组的信息码元相关，而且还和与本码组相邻的前若干码组的信息码元也有约束关系，则这类码称为卷积码。

(2) 根据码字中的信息元是否发生变化，可分为系统码与非系统码。在系统码中，编码后的信息码元保持原样不变，而非系统码中信息码元则改变了原有的形式。在分组码情况下系统码与非系统码性能相同，因此更多地采用系统码；在卷积码的情况下有时非系统码有更好的性能。

(3) 根据构造编码的数学方法，可分为代数码、几何码和算术码。代数码建立在近世代数的基础上，理论发展最为完善。

(4) 根据监督码元和信息码元的关系，可分为线形码和非线形码。若编码规则可以用线性方程组来表示，则称为线性码。反之，若两者不存在线性关系，则称为非线性码。线性码是代数码的一个最重要分支。

(5) 根据码的功能可分为检错码、纠错码以及纠正删除错误的纠删码。但实际上这三类码并无明显区分，同一类码可在不同的译码方式下体现出不同的功能。

(6) 按照纠正错误的类型不同，可以分为纠正随机错误码和纠正突发错误码。前者主要用于发生零星独立错误的信道，而后者则用于对付以突发错误为主的信道。

2.2 卷积码简介

卷积码是一类很好的信道编码，是与分组码相对应的另一大类编码，卷积码与分组码的不同之处在于其编码器是有记忆的。

卷积码的译码算法可以分为代数译码和概率译码，代数译码基于代数结构，概率译码有序列译码与维特比译码。

在本论文中，根据编码器的关系实现卷积码的编码，用维特比译码算法实现卷积码的解码。维特比译码算法采用最大似然算法，能够

达到最佳的误码率，运算量的大小也完全能够被接受。维特比译码算法通过比较规定时刻各个支路中的路径需求最短距离，得到幸存路径，

然后在译码结束时选择最短的一条，反推这条幸存路径得到相应的译码输出。

本论文是用C实现一个给定编码方案的卷积码编码及其维特比译码。并通过实例加入的随机噪声来验证维特比译码算法的纠错能力。

2.2.1卷积码的基本概念及基本组成

卷积码是1955年埃里亚斯（Elias）最早提出的，1957年伍成克拉夫（Wozencraft）提出了一种有效的译码方法，即序列译码。1963年梅西（Massey）提出了一种性能稍差，但比较实用的门限译码方法。门限译码是一种代数译码法，其主要特点是算法简单，易于实现。为译出每一个信息元所需的译码运算时间是个常数，即译码延时是固定的。这一特性使卷积码从理论走向实用化。而后1967年维特比（Viterbi）提出了最大似然译码法。它对存储器级数较小的卷积码的译码很容易实现，人们后来称它为维特比算法或维特比译码，并被广泛地应用于现代通信中。序列译码和维特比最大似然译码都是概率译码，序列译码的延时是随机的，它与信道干扰情况有关。而维特比最大似然译码的运算时间是固定的，其译码的复杂性（无论是硬件实现还是软件实现）均随m按指数增长。但是随着大规模集成电路技术的发展，这些已不是妨碍维特比译码或序列译码广泛应用的关键因素。

2.2.2 卷积码编码器的形成

卷积码是用移位寄存器实现编码的，如图2-1所示。被编码的数据流以K0个信息元分组，称作一帧，由m+1 帧数据相关输出n0个码元的一个码帧，其中m为移位寄存器的帧存储级数。其工作流程是以帧为单位操作的，每读入一帧“新”数据，移位寄存器中的“老”数据就向右移一帧，编码逻辑单元（又称函数发生器）“计算”并输出一个个n0长的码帧，所以码率为R=K0/n0。

由编码过程可见，虽然码字是一帧一帧输出的，但每一帧码字都是由L=m+1帧数据参与“计算”的。因此，每帧数据从第一次输入并参与编码开始到从移位寄存器移出，共参与了L次编码，称L=m+1为卷积码的编码约束度，它表示编码过程中互相关联的码帧个数。而互相关联（或称约束）的码元个数Ln0=NA被称为编码约束长度。可见除了码率R以外，m，L和NA也是表征卷积码的重要参数。因此，常用（n0，K0，m）来表示卷积码。

类似地，在译码过程中也要关联到md个码帧，才能译出一个信息帧，通常md≥m，称Ld=md+1为译码约束度，而相应的码元个数n0Ld为译码约束长度。它们也分别表示译码过程中相互约束的码帧以及码元个数。

图2-1卷积码编码器

2.2.3 卷积码编码的基本原理

分组码和卷积码主要差别在于卷积码编码器有记忆，且在任意给定的时段，编码器的n0个输出不仅与此时段的K0个输入有关，而且也与前m0个输入（记忆器件中存储的）有关。因此卷积码一般可采用（n0,k0,m0）来表示，其中K0为输入码元数，n0为输出码元数，而m0则为编码器的存储器数。典型的卷积码一般选较小的n0和k0（k0<n0），但存储器m0则取较大的值（m0<10），已获得既简单又高性能的信道编码。卷积码的编码器是由一个有k0个输入端、n0个输出端、m0节移位寄存器所构成的有限状态的有记忆系统，通常称它为时序网络。描述这类时序网络的方法很多，大致可分为两大类型：解析表示法与图形表示法。解析法又可分为离散卷积法、生成矩阵法、码多项式法等；图形表示法可分为状态图法、树图法、格图法等。描述卷积码编、译码的过程，可以用不同的描述方法，如矩阵法、码树法、状态图法和篱状图法等。采用何种方法描述卷积码的编码器，与其译码方法有很大关系。例如，在代数译码时，用矩阵法对译码原理的叙述和理解较方便。而借助树码和篱状图能更为清晰地分析和了解概率译码的过程和码的性能。类似（n，k）线性分组码，卷积码也用生成矩阵和监督矩阵来描述。

2.2.4 卷积码编码过程的图形描述

1. 树状图

用图形描述卷积码的编码过程比较直观。图2-1是L=3，R=7/3的（3，1，2）二进制卷积码编码器。输入帧长k0=1，输出码帧长n0=3，而编码器的存储级数m0=2，共有三个移位寄存器D0，D1，D2组成。

图2-1 卷积码（3，1，2）编码器

图2-2是图2-1编码器编码过程的图形描述，称为树状图（treediagram）。该图由结点和称之为树枝的连线组成，最初结点成为根结点。编码过程从根结点开始，根据输入信息元是0或1在结点处分叉。图2-2表示的分叉规律为：输入比特为0，取上分支；输入比特为1，取下分支。树枝上标注输出的码字。结点a，b，c，d是码字输出后移位寄存器D0D1的状态，也是编码器所处的状态，它们分别为00，01，10，11对应于a，b，c，d。在移位脉冲作用下，输入新的信息元，D0D1状态右移变成D1D2状态，然后与新输入的D0状态共同按编码逻辑输出第二个编码帧码字。这个过程由一条树枝代表，新的D0D1状态由到达的新的结点表示。这样，根据输入序列，可在树状图中沿序列指定的途径，从树根到某一树枝而得到（3，1，2）卷积码的码字。

图2-2卷积码（3，1，2）树状图

2. 网格图

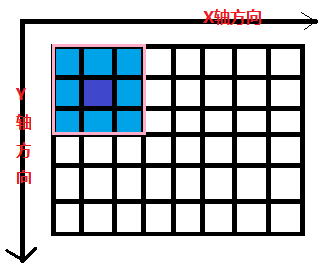
考察图2-2树状图的标记，就会发现第三次编码输出后到达的状态标注abcd，在虚线上部与下部是一样的。由于编码逻辑不变，对相同的D0D1状态其输出也是一样的，比如对所有结点a后面的2组输出总是000（输入信息元为0）和111（输入信息元为1）；对结点c后的输出码字总是001和110；对结点b和d也有相同的特点。正因为如此，在图2-2中省去了第三级以后对输出码的标注。那么结点也可以省吗？既然有同样标记的结点（即状态相同）分叉出去的分支总是相同的，意味着这些个结点可以合并。图2-2表示的是m=2，L=3的编码器的树状图，最多状态只有4个，如果将所有结点都合并成a，b，c，d四个状态，就得到另一种更紧凑的图，叫网格图（trellis diagram）。图2-3就是对应的网格图。在画网格图时，约定用实线表示输入比特为0时产生的输出，虚线表示输入比特为1时产生的输出。

图2-3 卷积码网格图

由图可见，在初始瞬态之后每一时间单位，网格向右延伸一级。网格图的每一级包括4个结点，每个结点意味着寄存器a，b，c，d四个状态之一。在第二级之后，网格图中每个结点有两条进路和两条出路。当然，两条出路中，一条对应于输入为0，另一条则对应于输入为1。

3. 状态图

由于编码器的输出取决于输入和编码器的状态，所以还有一个比网格图更紧凑的状态图（statediagram）。但是状态图只不过是一种表示编码器可能状态及由一个状态到另一状态可能转移的图形，并不能表示状态转移与时间的关系。例如，图2-4就是图2-1编码器的状态图。图中，每个分支旁边标明的3bit码字表示输出比特，虚线表明输入比特为1，实线表明输入比特为0。

对于一般的（n0,k0,m）卷积码，其特点是树状图的每一个结点散发出2^k0个分支。其网格图和状态图都具有2^k0m个可能状态。每个状态有2^k0个分支进入，而散发出2^k0个分支（在网格图和树状图中，上述结论在初始瞬态之后才正确）。

图2-4（3，1，2）卷积码状态图

3Viterbi译码

1965年Andrew.Viterbi提出了一种概率译码算法，称为Viterbi译码或简称VB译码。这是一种不同于只考虑码字的代数结构的译码方法，它还结合了信道的统计特性，是一种最大似然译码，在二进制对称信道时也就是最小距离译码。

关于卷积码的译码方法有多种，Wozencraft所提出的序列译码，梅西所提出的门限译码方法，门限译码的是一种代数译码法，其主要特点是算法简单，易于实现，译码时间是固定的。在此次毕业设计中，我采用的译码方法是目前极为广泛的应用于现代通信中的Viterbi译码，它是Viterbi在1967年提出，是一种最大似然译码法，其译码时间是固定的，特别适用于存储器级数较小的卷积码译码。Viterbi译码的方法是卷积码网格图和汉明距相结合译码的。

由于信息在不同的信道中传播过程中，会受到外界突发因素的影响难免会使接收端的码字产生错误，所以在译码器设计过程中，也将对译码器的纠错性能加以考虑并会在论文中给与讨论。

3.1Viterbi译码度量

由编码过程可知，向编码器输入信息序列M，就有码序列C从编码器输出，经过调制而送入信道传输。由于信道噪声的存在，会在传输过程中引入信道错误序列E，使译码器的输入序列为R=C+E。若E=0，则R=C就是发送的码字。不同的E，就会有不同的R，它们与发送码字C的汉明距离也就不相同。译码算法就是寻找与R有最小码距的一个C^作为发送码字C的最佳估计而纠正一定的错误。若C^就是发送的C，则错误全部被纠正。

那么，如何定量地计算码距呢？为此，定义了度量。对任一个码序列C，定义条件概率P（R/C）的对数为码序列C的度量或路径度量，这是因为每个码序列都对应于编码网格图上的一条路径。用M（R/C）表示度量，即

M（R/C）=㏒P（R/C）

对二进制对称信道而言，计算和寻找有最大度量的路径与寻找与R有最小Hamming距离的C是等价的。即mind（R，C）与maxM（R/C）是等效的。于是，译码问题就归结为寻找与接收码字R有最大路径度量的码字C。

3.2实现Viterbi译码算法的具体考虑

3.2.1 卷积码距离特性

卷积码的性能取决于卷积码距离特性和译码算法，其中距离特性是卷积码自身本质的属性，它决定了该码潜在的纠错能力，而译码算法是个如何将潜在纠错能力转化为实际纠错能力的问题。为此，了解卷积码距离特性是必要的。

描述距离特性的最好方法是利用网格图。设序列C1、C2是同一时刻从同一状态出发的任意两个不同的二进制码字序列，不失一般性不妨设0时刻从0状态出发。序列距离定义为两序列C1和C2在对应时刻的码字的汉明距离之和，即两序列模2加后的重量。任意两序列的最小距离叫做自由距离df，根据定义，自由距离在网格图上就是0时刻从0状态与全零路径分叉（C≠0）、经若干分支后又回到全零路径（与全零序列距离不再继续增大）的所有路径中，重量最轻（与全零序列距离最近）那条路径的重量。

3.2.2 卷积码的译码算法

前面我们已经讨论过，分组码的纠错能力取决于码的最小距离，分组码的最大似然译码实际上就是最小距离译码。这些准则同样也适用于卷积码，不同之处在于，分组码是孤立地考虑各分组的距离，而卷积码是通盘考虑整个序列的距离。卷积码自由距离df的计算有很多方法，简单卷积码可以直接在网格图上推得；稍微复杂一些的卷积码可采用信号留图法，它也具有理论价值；而最实用的方法还是靠编程利用计算机来搜索。

关于卷积码的译码方法有多种，Wozencraft所提出的序列译码，梅西所提出的门限译码方法，门限译码的是一种代数译码法，其主要特点是算法简单，易于实现，译码时

爱华网本文地址 » http://www.aihuau.com/a/25101010/31174.html