一、类比估算、参数估算、自下而上估算、三点估算
这些技术有规律性的出现在有关“估算”的相关过程,这些过程都有专家判断。
类比估算Analogous Estimating[Technique
以过去类似活动的参数值(如范围、成本、预算和持续时间等)或规模指标(如尺寸、重量和复杂性等)为基础,来估算未来活动的同类参数或指标的估算技术。
这是一种粗略的估算方法,有时需根据项目复杂性方面的已知差异进行调整。该方法综合利用历史信息和专家判断,常用在项目的早期阶段。
相对于其他估算技术,类比估算通常成本较低、耗时较少,但准确性也较低。如果以往活动是本质上而不只是表面上类似,并且从事估算的项目团队成员具备必要的专业知识,那么类比估算就最为可靠。
参数估算[技术] ParametricEstimating [Technique]
利用历史数据与其他变量(如建筑施工中的平方英尺、软件开发中的代码行数)之间的统计关系来估算诸如范围、成本、预算和持续时间等活动参数的一种估算技术。例如,进行成本参数估算,就可把计划工作量乘以历史单位成本,得出成本估算值。
参数估算的准确性取决于参数模型的成熟度和基础数据的可靠性。
自下而上估算[技术] Bottom upEstimating [Technique]:
对工作组成部分进行估算的一种方法。先把工作分解为更细节的部分,再对低层次上每个细节部分所需的投入进行估算,最后汇总得到整个工作所需的总投入。
该估算方法的准确性取决于较低层次上的工作的规模和复杂程度。
类比估算 | 参数估算 | 自下而上估算 | 三点估算 |
6.4估算活动持续时间 7.1估算成本 | 6.4估算活动持续时间 7.1估算成本 | 6.3估算活动资源 7.1估算成本 | 6.4估算活动持续时间 7.1估算成本 |
综合利用历史信息和专家判断 | 利用历史数据与其他变量 | ||
粗略的估算方法 | 最准确 | ||
用于项目的早期阶段 | |||
成本较低 耗时较少 | 成本较低 耗时较少 | 成本高 耗时长 | |
但准确性也较低 | 准确性取决于参数模型的成熟度和基础数据的可靠性 | 确性取决于较低层次上的工作的规模和复杂程度 | 计算出来的持续时间可能更加准确。 |
三点估算[技术] Three Point Estimate[Technique]:
通过考虑估算中的不确定性和风险,可以提高活动持续时间估算的准确性。这个概念起源于计划评审技术(PERT)。PERT 使用 3种估算值来界定活动持续时间的近似区间:
最可能时间(Tm)。基于最可能获得的资源、最可能取得的资源生产率、对资源可用时间的现实预计、资源对其他参与者的可能依赖以及可能发生的各种干扰等,所得到的活动持续时间。
最乐观时间(To)。基于活动的最好情况,所得到的活动持续时间。
最悲观时间(Tp)。基于活动的最差情况,所得到的活动持续时间。
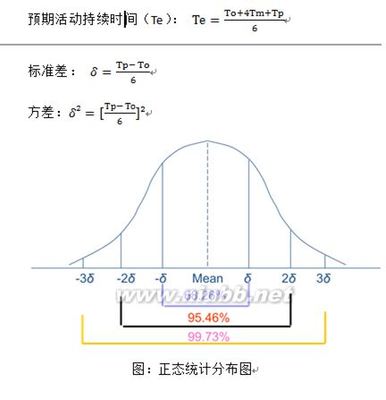
PERT 分析方法对以上 3 种估算进行加权平均,来计算:
根据正态统计分布图,预期活动持续时间(Te)表示50%概率的可能性在该工期完成。工期落在预期活动持续时间1个标准差的范围之间的概率是68.26%,落在2个标准差的范围之间的概率是95.46%,在3个标准差的范围之间的概率是99.73%。
二、题解,一个活动预期活动持续时间是10天,而标准差是2天:
范围 | 工期范围(天) | 概率 |
±1δ | 8~12 | 68.26% |
±2δ | 6~14 | 95.46% |
±3δ | 4~16 | 99.73% |
-∞~1δ | 12天内完成 | 50%+68.26%/2 =84.13% |
-∞~-2δ | 6天内完成 | 50%-95.46%/2 =2.27% |
三:提升:
3.1 概念
如果计算项目的工期,可以把关键路径上的全部活动的预期活动持续时间全部相加,得到项目的平均工期。如果需要计算特定标准差范围的项目工期,则需要将这些活动的方差之和后开平方得到项目工期的标准差。注意:
只有同一条关键路径上的活动工期才能相加
各项活动的标准差不能相加,只有方差才能相加。
用以上公式(甚至用该 3 种估算的简单平均公式)计算出来的持续时间可能更加准确。这 3种估算能表明持续时间估算的变化范围。三点估算可用于估算成本过程。
3.2 例题:
1)仅用上图活动的逻辑关系,活动持续时间用下表的数值,决定此项目最短的完成完工时间是?
活动 | To | Tm | Tp | Te、、 |
A | 1 | 2 | 3 | |
B | 3 | 5 | 13 | |
C | 2 | 3 | 4 | |
D | 1 | 2 | 3 | |
E | 0.5 | 1 | 1.5 | |
F | 0.5 | 1 | 1.5 | |
G | 3 | 5 | 8 | |
H | 0.5 | 1 | 1.5 | |
I | 1 | 2 | 3 |
A、BCDEI 13
B、BCDEI 14
C、BGHI 14
D、BCDI 13
2) 参照第1)题,16天完工概率是?
A、68.26%
B、84.13%
C、97.73%
D、95.46%
解析:
1) C
题干“决定此项目最短的完成完工时间是”就是通过网络图找出关键路径,通过三点估算首先算出每个活动的持续时间Te,发现关键路径为BGHI14天。只有同一条关键路径上的活动工期才能相加。
活动 | To | Tm | Tp | Te | 标准差 | 方差 |
A | 1 | 2 | 3 | 2 | 1/3 | (1/3)² |
B | 3 | 5 | 13 | 6 | 5/3 | (5/3)² |
C | 2 | 3 | 4 | 3 | 1/3 | (1/3)² |
D | 1 | 2 | 3 | 2 | 1/3 | (1/3)² |
E | 0.5 | 1 | 1.5 | 1 | 1/6 | (1/6)² |
F | 0.5 | 1 | 1.5 | 1 | 1/6 | (1/6)² |
G | 2 | 5 | 8 | 5 | 1 | 1 |
H | 0.5 | 1 | 1.5 | 1 | 1/6 | (1/6)² |
I | 1 | 2 | 3 | 2 | 1/3 | (1/3)² |
2) B
如果计算项目的工期,可以把关键路径上的全部活动的预期活动持续时间全部相加,得到项目的平均工期。如果需要计算特定标准差范围的项目工期,则需要将这些活动的方差之和后开平方得到项目工期的标准差。
注意:各项活动的标准差不能相加,只有方差才能相加。
所以关键路径的方差之和等于141/36,开平方求出标准差是≈2,题干在16天内完成的概率既是区间(负无穷到1个西格玛所构成的面积):
16天完成概率=50%+68.26%/2=84.13%
注意:
1、对三点估算考题,在简单的题,要学会用草稿画出简单的网络图,用笔代替脑袋;
2、对正态分布概率计算,注意用草稿画出正态分布图,用面积的方法求得需要的概率。
 爱华网
爱华网



