以前在博客上放的基二FFT源程序,可读性是比较差的,现在已经改过程序,从新发上去了。这几天仔细的研究了一下基二FFT算法,受益非浅。现在简单的分析一下基二算法的原理。在VISIO里画了程序框图,呵呵。可是不知道怎么传上来,最后还是存为BMP格式的,传了上来。希望对大家有所帮助。源程序见我的另一篇文章《基二FFT的C语言实现》
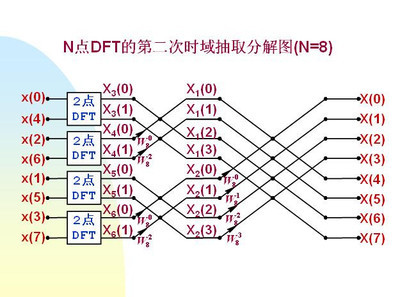
当N太大时,直接进行DFT运算,运算量会很大,这就对计算机的性能提出了很高的要求。但是利用周期性可以大大的降低运算量。利用周期性,可将N点DFT分解为两个N/2点的DFT。同理可以对x(n)进行继续分解,依次类推经过M-1次分解,最后将N点DFT分解成N/2个2点的DFT。N点DFT的一次时域分解图如图1
根据DFT的基二分解方法,可以发现在第L(L表示从左到右的运算级数,L=1,2,3…M)级中,每个蝶形的两个输入数据相距个点,同一旋转因子对应着间隔为2^L点的2^(M-L)个蝶形。从输入端开始,逐级进行,共进行M级运算。在进行L级运算时,依次求出个2^(L-1)不同的旋转因子,每求出一个旋转因子,就计算完它对应的所有的2^(M-L)个蝶形。因此我们可以用三重循环程序实现FFT变换。同一级中,每个蝶形的两个输入数据只对本蝶形有用,而且每个蝶形的输入、输出数据节点又同在一条水平线上,所以输出数据可以立即存入原输入数据所占用的存储单元。,这种方法可称为原址计算,可节省大量的存储单元。FFT算法的程序框图如图2
FFT算法的输出X(K)为自然顺序,但为了适应原位计算,其输入序列不是按x(n)的自然顺序排序,这种经过M-1次奇偶抽选后的排序为序列的倒序。因此,在运算之前应先对序列x(n)进行倒序。倒序的规律就是把顺序数的二进制位倒置,即可得到倒序值。倒序数是在M位二进制数最高位加一,逢2向右进位。对于,M位二进制数最高位的权值为N/2,且从左到右二进制位的权值依次为你N/4,N/8,···,2,1。因此,最高位加一相当于十进制运算J+N/2。(J
详细的解释请参考西安电子科学技术大学出版的《数字信号处理》
程序void FFT(float data[],int n,int ok)//声明FFT函数
{
int mmax,m,j,step,i;
double temp;
double theta,sin_htheta,sin_theta,pwr,wr,wi,tempr,tempi;
n=2*(1<<n);
int nn=n>>1;
// 第一步:整理位序颠倒的次序
j=1;
for(i=1;i<n;i+=2)
{
if(j>i)
{ temp=data[j-1];
data[j-1]=data[i-1];
data[i-1]=temp;
temp=data[j];
data[j]=data[i];
data[i]=temp;
}
// 相反的二进制加法
m=nn;
while(m>=2&&j>m)
{
j-=m;
m>>=1;
}
j+=m;
}
// 程序的 Danielson - Lanczos 引理应用部分
mmax=2;
while(n>mmax) //log2(n)次循环
{
step=mmax<<1;
theta=ok*DOUBLE_PI/mmax; //三角递归初始赋值
sin_htheta=sin(0.5*theta);
sin_theta=sin(theta);
pwr= -2.0*sin_htheta*sin_htheta;
wr=1.0;
wi=0.0;
for(m=1;m<mmax;m+=2)
{
for(i=m;i<=n;i+=step)//以下不是很理解,请指点
{
j=i+mmax;
tempr=wr*data[j-1]-wi*data[j];
tempi=wr*data[j]+wi*data[j-1];
data[j-1]=data[i-1]-tempr;
data[j]=data[i]-tempi;
data[i-1]+=tempr;
data[i]+=tempi;
}
wr=(sin_htheta=wr)*pwr-wi*sin_theta+wr;
wi=wi*pwr+sin_htheta*sin_theta+wi; //三角递归
}
mmax = step;
}
}
其中部分代码不是很理解,请指点,谢谢你 xiao1dian@163.comRe: 基二FFT的原理和算法 [8/29/2007 7:29:59 AM]很好的文章,通俗易懂,但是我看了你的c语言程序,不知道你用的什么嵌入式系统,数据处理能力有这么强啊?我用xilinx的MicroBlaze做嵌入式,像你程序里的cos,sin和pow()函数肯定是跑不起来的,需要n大的一片程序ram,你用什么做的嵌入式啊?Re: 基二FFT的原理和算法 [8/2/2007 12:34:49 PM]
 爱华网
爱华网