在数学上一个连续概率密度函数p(x)的需满足以下的条件:1、x在a和b之间的概率为:
2、对所有的x,p(x)非负3、p(x)的积分值为1
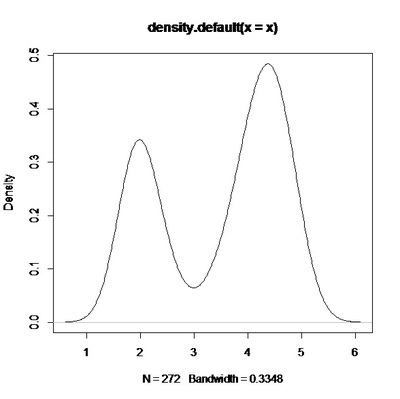
最经常使用的概率密度函数就是高斯函数(正态分布)
将一维的情况扩展到多维,现在的x就是一个向量,p(x)也需要满足下列条件:1、在一个区域R内x的概率为
2、概率密度函数的积分值为1
密度估计
给点n个数据样本x1,x2,....,xn,我们可以估计概率密度函数p(x),对于新的样本x就可以计算出相应的p(x).这个过程就是密度估计。密度估计的基础是:一个向量x落入到区域R的概率为假设R非常小,所以p(x)的变化也很小,上面的公式就改写为:
其中V是R的“体积”另一方面,假设x1,...,xn是根据密度函数p(x)独立取的n个样本点,其中有k个样本点落入到区域R中,关于R的概率就为:这样就可以得到一个p(x)的估计函数:Parzen window密度估计假设R是以x为中心的超立方体,h为这个超立方体的边长,在2-D的方形中有V=h*h,3-D的立方体中有V=h^3。
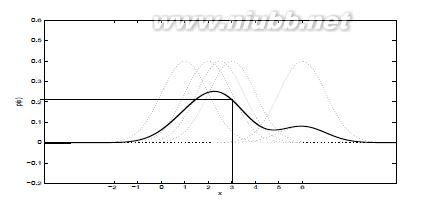
给定上面的公式,表示的是Xi是否落在方形中。Parzen概率密度估计公式的表示如下:其中被称作窗口函数(windowfunction)。同时可以对窗口函数做一定的泛化,就有其他的Parzen window密度估计方法。例如在1-D的情况下使用Gaussian函数:这种方法就相当于将n个点为中心的高斯函数计算平均。其中标准差需要预先设定。例子:给定五个点:x1=2, x2=2.5, x3=3, x4=1, x5=6,计算x=3位置的Parzen概率密度函数,采用的高斯函数作为windowfunction。计算过程如下:
采用图形的方式进行显示,并假设上面的5个点对整个密度函数做出相等的贡献:采用Parzen Window对这个五个点估计得到的概率密度函数为:
 爱华网
爱华网