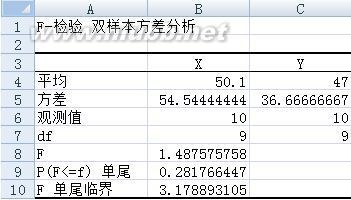
用来测试某一个控制变量的不同水平是否给观察变量造成显著差异和变动。
方差分析前提:不同水平下,各总体均值服从方差相同的正态分布。所以方差分析就是研究不同水平下各个总体的均值是否有显著的差异。统计推断方法是计算F统计量,进行F检验,总的变异平方和 SST,控制变量引起的离差SSA(Between Group离差平方和),另一部分随机变量引起的SSE(组内Within Group离差平方和),SST=SSA+SSE。
spss教程:单因素方差分析——方法/步骤spss教程:单因素方差分析 1、
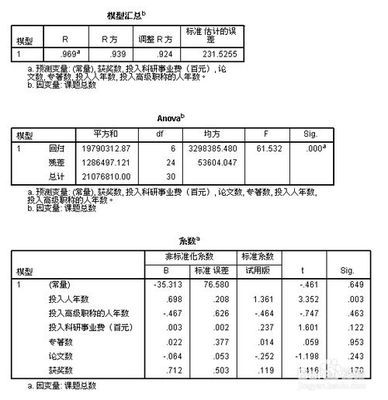
计算检验统计量的观察值和概率P_值:Spss自动计算F统计值,如果相伴概率P小于显著性水平a,拒绝零假设,认为控制变量不同水平下各总体均值有显著差异,反之,则相反,即没有差异。
spss教程:单因素方差分析 2、
方差齐性检验:控制变量不同水平下各观察变量总体方差是否相等进行分析。采用方差同质性检验方法(Homogeneity of variance),原假设“各水平下观察变量总体的方差无显著差异,思路同spss两独立样本t检验中的方差分析”。 图中相伴概率0.515大于显著性水平0.05,故认为总体方差相等。
趋势检验:趋势检验可以分析随着控制变量水平的变化,观测变量值变化的总体趋势是怎样的,线性变化,二次、三次等多项式。趋势检验可以帮助人们从另一个角度把握控制变量不同水平对观察变量总体作用的程度。图中线性相伴概率为0小于显著性水平0.05,故不符合线性关系。
spss教程:单因素方差分析_方差分析
spss教程:单因素方差分析 3、
多重比较检验:单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响,多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何,那个水平显著,哪个不显著。常用LSD、S-N-K方法。LSD方法检测灵敏度是最高的,但也容易导致第一类错误(弃真)增大,观察图中结果,在LSD项中,报纸与广播没有显著差异,但在别的方法中,广告只与宣传有显著差异。
spss教程:单因素方差分析_方差分析
spss教程:单因素方差分析 4、
相似性子集:由图可知,划分的子集结果是一样的。通常在相似性子集划分时多采用S-N-K方法的结论。其结论可以与上述多重比较检验结合起来看,验证在LSD项中,报纸与广播没有显著差异的结论。
 爱华网
爱华网