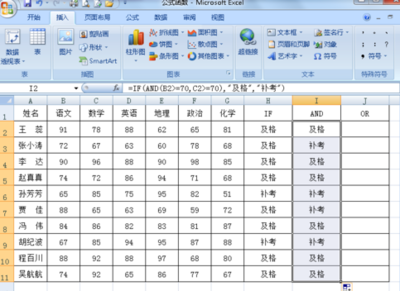
Forbrevity. Takeout the sameparagraphs, and let it to be lemma, theorem.
In mathematics, a theorem is a statement that has been proven on the basis of previously establishedstatements, such as other theorems, and previously acceptedstatements, such as axioms. The derivation of a theorem is ofteninterpreted as a proof of the truth of the resulting expression,but different deductive systems can yield otherinterpretations, depending on the meanings of the derivation rules.Theorems have two components, called the hypotheses and the conclusions. The proof of amathematical theorem is a logical argument demonstrating that theconclusions are a necessary consequence of the hypotheses, in thesense that if the hypotheses are true then the conclusions mustalso be true, without any further assumptions. The concept of atheorem is therefore fundamentally deductive, in contrast to the notion of ascientific theory, which is empirical.[2]
Although they can be written in a completely symbolic formusing, for example, propositional calculus, theorems are oftenexpressed in a natural language such as English. The same is trueof proofs, which are often expressed as logically organized andclearly worded informal arguments, intended to convince readers ofthe truth of the statement of the theorem beyond any doubt, andfrom which arguments a formal symbolic proof can in principle beconstructed. Such arguments are typically easier to check thanpurely symbolic ones — indeed, many mathematicians would express apreference for a proof that not only demonstrates the validity of atheorem, but also explains in some way why it is obviouslytrue. In some cases, a picture alone may be sufficient to prove atheorem. Because theorems lie at the core of mathematics, they arealso central to its aesthetics. Theorems are often described asbeing "trivial", or "difficult", or "deep", or even "beautiful".These subjective judgments vary not only from person to person, butalso with time: for example, as a proof is simplified or betterunderstood, a theorem that was once difficult may become trivial.On the other hand, a deep theorem may be simply stated, but itsproof may involve surprising and subtle connections betweendisparate areas of mathematics. Fermat's Last Theorem is a particularlywell-known example of such a theorem.
Contents[hide] |
[edit]Informal accounts of theorems
Logically, many theorems are of the form of anindicative conditional: if A, then B.Such a theorem does not state that B is always true, onlythat B must be true if A is true. In this caseA is called the hypothesis of the theorem (note that"hypothesis" here is something very different from a conjecture) and B the conclusion(A and B can also be denoted the antecedentand consequent). The theorem "If n is an evennatural number then n/2 is a naturalnumber" is a typical example in which the hypothesis is that"n is an even natural number" and the conclusion is that"n/2 is also a natural number".
In order to be proven, a theorem must be expressible as aprecise, formal statement. Nevertheless, theorems are usuallyexpressed in natural language rather than in a completely symbolicform, with the intention that the reader will be able to produce aformal statement from the informal one.
It is common in mathematics to choose a number of hypothesesthat are assumed to be true within a given theory, and then declarethat the theory consists of all theorems provable using thosehypotheses as assumptions. In this case the hypotheses that formthe foundational basis are called the axioms (or postulates) of thetheory. The field of mathematics known as proof theory studies formal axiom systems andthe proofs that can be performed within them.
A planar map with five colors such that no tworegions with the same color meet. It can actually be colored inthis way with only four colors. The four color theorem states that such coloringsare possible for any planar map, but every known proof involves acomputational search that is too long to check by hand.Some theorems are "trivial," in the sense that they follow fromdefinitions, axioms, and other theorems in obvious ways and do notcontain any surprising insights. Some, on the other hand, may becalled "deep": their proofs may be long and difficult, involveareas of mathematics superficially distinct from the statement ofthe theorem itself, or show surprising connections betweendisparate areas of mathematics.[3] Atheorem might be simple to state and yet be deep. An excellentexample is Fermat's Last Theorem, and there are many other examplesof simple yet deep theorems in number theory and combinatorics, among other areas.
There are other theorems for which a proof is known, but theproof cannot easily be written down. The most prominent examplesare the four color theorem and the Kepler conjecture. Both of these theorems areonly known to be true by reducing them to a computational searchwhich is then verified by a computer program. Initially, manymathematicians did not accept this form of proof, but it has becomemore widely accepted in recent years. The mathematician Doron Zeilberger has even gone so far as toclaim that these are possibly the only nontrivial results thatmathematicians have ever proved.[4]Many mathematical theorems can be reduced to more straightforwardcomputation, including polynomial identities, trigonometricidentities and hypergeometric identities.[5][pageneeded]
[edit]Relation toproof
The notion of a theorem is deeply intertwined with the conceptof proof. Indeed, theorems are true precisely in the sense thatthey possess proofs. Therefore, to establish a mathematicalstatement as a theorem, the existence of a line of reasoning fromaxioms in the system (and other, already established theorems) tothe given statement must be demonstrated.
Although the proof is necessary to produce a theorem, it is notusually considered part of the theorem. And even though more thanone proof may be known for a single theorem, only one proof isrequired to establish the theorem's validity. The Pythagoreantheorem and the law of quadratic reciprocity are contenders for thetitle of theorem with the greatest number of distinct proofs.
[edit]Theorems inlogic
| This section needs additional citations for verification. Please help improve this article by addingcitations to reliable sources. Unsourcedmaterial may be challenged and removed. (October2010) |
| The neutrality of this section is disputed. Please see the discussion on thetalk page. Please do not remove this messageuntil the dispute is resolved.(October 2010) |
Logic, especially in the field of prooftheory, considers theorems as statements (called formulas or well formed formulas) of a formallanguage. The statements of the language are strings of symbols andmay be broadly divided into nonsense and well-formed formulas. A set ofdeduction rules, also called transformation rules orrules of inference, must be provided. Thesededuction rules tell exactly when a formula can be derived from aset of premises. The set of well-formed formulas may be broadlydivided into theorems and non-theorems. However, according toHofstadter, a formal system will often simplydefine all of its well-formed formula as theorems.[6][pageneeded]
Different sets of derivation rules give rise to differentinterpretations of what it means for an expression to be a theorem.Some derivation rules and formal languages are intended to capturemathematical reasoning; the most common examples use first-order logic. Other deductive systemsdescribe term rewriting, such as the reduction rulesfor λ calculus.
The definition of theorems as elements of a formal languageallows for results in proof theory that study the structure offormal proofs and the structure of provable formulas. The mostfamous result is Gödel's incompleteness theorem; by representingtheorems about basic number theory as expressions in a formallanguage, and then representing this language within number theoryitself, Gödel constructed examples of statements that are neitherprovable nor disprovable from axiomatizations of numbertheory.
[edit]Relation with scientific theories
Theorems in mathematics and theories in science arefundamentally different in their epistemology. A scientific theory cannot beproven; its key attribute is that it is falsifiable, that is, it makes predictionsabout the natural world that are testable by experiments. Any disagreement betweenprediction and experiment demonstrates the incorrectness of thescientific theory, or at least limits its accuracy or domain ofvalidity. Mathematical theorems, on the other hand, are purelyabstract formal statements: the proof of a theorem cannot involveexperiments or other empirical evidence in the same way suchevidence is used to support scientific theories.
The Collatz conjecture: one way to illustrate itscomplexity is to extend the iteration from the natural numbers tothe complex numbers. The result is a fractal, which (in accordancewith universality) resembles the Mandelbrot set.Nonetheless, there is some degree of empiricism and datacollection involved in the discovery of mathematical theorems. Byestablishing a pattern, sometimes with the use of a powerfulcomputer, mathematicians may have an idea of what to prove, and insome cases even a plan for how to set about doing the proof. Forexample, the Collatz conjecture has been verified for start valuesup to about 2.88 × 1018. TheRiemann hypothesis has been verified for thefirst 10 trillion zeroes of the zeta function. Neither of these statements isconsidered to be proven.
Such evidence does not constitute proof. For example, theMertens conjecture is a statement aboutnatural numbers that is now known to be false, but no explicitcounterexample (i.e., a natural number n for which theMertens function M(n) equals or exceeds the squareroot of n) is known: all numbers less than1014 have the Mertens property,and the smallest number which does not have this property is onlyknown to be less than the exponential of 1.59 × 1040, which is approximately 10 to the power 4.3 ×1039. Since the number ofparticles in the universe is generally considered to be less than10 to the power 100 (a googol), there is no hope to find an explicitcounterexample by exhaustive search.
Note that the word "theory" also exists in mathematics, todenote a body of mathematical axioms, definitions and theorems, asin, for example, group theory. There are also "theorems" inscience, particularly physics, and in engineering, but they oftenhave statements and proofs in which physical assumptions andintuition play an important role; the physical axioms on which such"theorems" are based are themselves falsifiable.
[edit]Terminology
A number of different terms for mathematical statements exist,these terms indicate the role statements play in a particularsubject. The distinction between different terms is sometimesrather arbitrary and the usage of some terms has evolved overtime.
There are other terms, less commonly used, which areconventionally attached to proven statements, so that certaintheorems are referred to by historical or customary names. Forexamples:
A few well-known theorems have even more idiosyncratic names.The division algorithm is a theorem expressingthe outcome of division in the natural numbers and more generalrings. The Banach–Tarski paradox is a theorem in measure theory that is paradoxical in the sense that it contradictscommon intuitions about volume in three-dimensional space.
An unproven statement that is believed to be true is called aconjecture (or sometimes a hypothesis, but with adifferent meaning from the one discussed above). To be considered aconjecture, a statement must usually be proposed publicly, at whichpoint the name of the proponent may be attached to the conjecture,as with Goldbach's conjecture. Other famousconjectures include the Collatz conjecture and the Riemannhypothesis.
[edit]Layout
A theorem and its proof are typically laid out as follows:
- Theorem (name of person who proved it and year ofdiscovery, proof or publication).
- Statement of theorem (sometimes called theproposition).
- Proof.
- Description of proof.
- End mark.
The end of the proof may be signalled by the letters Q.E.D. meaning "quod erat demonstrandum" or byone of the tombstone marks "□" or "∎" meaning"End of Proof", introduced by Paul Halmos following their usage in magazinearticles.
The exact style will depend on the author or publication. Manypublications provide instructions or macros for typesetting in the house style.
It is common for a theorem to be preceded by definitions describing the exact meaning ofthe terms used in the theorem. It is also common for a theorem tobe preceded by a number of propositions or lemmas which are thenused in the proof. However, lemmas are sometimes embedded in theproof of a theorem, either with nested proofs, or with their proofspresented after the proof of the theorem.
Corollaries to a theorem are either presented between thetheorem and the proof, or directly after the proof. Sometimescorollaries have proofs of their own which explain why they followfrom the theorem.
[edit]Lore
It has been estimated that over a quarter of a million theoremsare proved every year.[12]
The well-known aphorism, "A mathematician is a device for turning coffee intotheorems", is probably due to Alfréd Rényi, although it is often attributedto Rényi's colleague Paul Erdős (and Rényi may have been thinkingof Erdős), who was famous for the many theorems he produced, thenumber of his collaborations, and his coffeedrinking.[13]
The classification of finite simplegroups is regarded by some to be the longest proof of atheorem; it comprises tens of thousands of pages in 500 journalarticles by some 100 authors. These papers are together believed togive a complete proof, and there are several ongoing projects toshorten and simplify this proof.[14]Another theorem of this type is the Four color theorem whosecomputer generated proof is too long to be read by a human. It iscertainly the longest proof of a theorem whose statement can beeasily understood by a layman.
[edit]Formalized account of theorems
A theorem may be expressed in a formal language (or "formalized"). A formaltheorem is the purely formal analogue of a theorem. In general, aformal theorem is a type of well-formed formula that satisfies certainlogical and syntactic conditions. The notation S is often used to indicate thatS is a theorem.
Formal theorems consist of formulas of a formal language and the transformation rules of a formal system.Specifically, a formal theorem is always the last formula of aderivation in some formal system each formulaof which is a logical consequence of the formulas which came before itin the derivation. The initially accepted formulas in thederivation are called its axioms, and are the basis on whichthe theorem is derived. A set of theorems is called a theory.
What makes formal theorems useful and of interest is that theycan be interpreted as true propositions and their derivations may beinterpreted as a proof of the truth of the resulting expression. A set offormal theorems may be referred to as a formal theory. A theorem whose interpretation is atrue statement about a formal system is called a metatheorem.
[edit]Syntax andsemantics
Main articles:Syntax (logic) and Formal semantics (logic)The concept of a formal theorem is fundamentally syntactic, incontrast to the notion of a "true proposition" in which semantics are introduced. Different deductivesystems may be constructed so as to yield other interpretations,depending on the presumptions of the derivation rules (i.e.belief, justification or other modalities). The soundness of a formal system depends onwhether or not all of its theorems are also validities. A validity is a formula that istrue under any possible interpretation, e.g. in classicalpropositional logic validities are tautologies. A formal system is consideredsemantically complete when all of itstautologies are also theorems.
[edit]Derivationof a theorem
Main article: Formal proofThe notion of a theorem is very closely connected to its formalproof (also called a "derivation"). To illustrate how derivationsare done, we will work in a very simplified formal system. Let uscall ours Its alphabet consists only of two symbols { A, B }and its formation rule for formulas is:
- Any string of symbols of which is at least 3 symbols long, and which is not infinitelylong, is a formula. Nothing else is a formula.
The single axiom of is:
- ABBA
The only rule of inference (transformation rule) for is:
- Any occurrence of "A" in a theorem may be replaced by anoccurrence of the string "AB" and the result is atheorem.
Theorems in are defined as those formulae which have a derivation ending withthat formula. For example
- ABBA (Given as axiom)
- ABBBA (by applying the transformation rule)
- ABBBAB (by applying the transformation rule)
is a derivation. Therefore "ABBBAB" is a theorem of The notion of truth (or falsity) cannot be applied to the formula"ABBBAB" until an interpretation is given to its symbols.Thus in this example, the formula does not yet represent aproposition, but is merely an empty abstraction.
Two metatheorems of are:
- Every theorem begins with "A".
- Every theorem has exactly two "A"s.
[edit]Interpretation of a formal theorem
Main article: Interpretation (logic)[edit]Theorems andtheories
Main articles:Theory and Theory (mathematical logic)[edit]See also
| Logic portal |
[edit]Notes
- ^ For full text of 2nd edition of 1940, seeElisha Scott Loomis. "The Pythagorean proposition:its demonstrations analyzed and classified, and bibliography ofsources for data of the four kinds of proofs".Education Resources InformationCenter. Institute of Education Sciences (IES) of the U.S. Department of Education.http://www.eric.ed.gov/PDFS/ED037335.pdf.Retrieved 2010-09-26. Originally published in 1940and reprinted in 1968 by National Council of Teachers ofMathematics.
- ^ However, both theorems and theories areinvestigations. See Heath 1897 Introduction, The terminology of Archimedes, p. clxxxii:"theorem (θεὼρνμα) fromθεωρεἳν to investigate"
- ^ Weisstein, Eric W., "Deep Theorem" fromMathWorld.
- ^ Doron Zeilberger. "Opinion51". http://www.math.rutgers.edu/~zeilberg/Opinion51.html.
- ^ Petkovsek et al. 1996.
- ^ Hofstadter 1980
- ^ Wentworth,G.; Smith, D.E. (1913). "Art. 46, 47". Plane Geometry. Ginn& Co..
- ^ Wentworth & Smith Art.50
- ^ Wentworth & Smith Art.51
- ^ Follows Wentworth &Smith Art. 79
- ^ The word law can also refer to anaxiom, a rule of inference, or, in probability theory, a probability distribution.
- ^ Hoffman 1998, p. 204.
- ^ Hoffman 1998, p. 7.
- ^ An enormous theorem: theclassification of finite simple groups, Richard Elwes,Plus Magazine, Issue 41 December 2006.
[edit]References
[edit]Externallinks
| Look up theorem in Wiktionary, the freedictionary. |
 爱华网
爱华网