标定参数描述[Description of thecalibration parameters]
标定之后 ,单击Save,参数清单会被保存在matlab文件Calib_Results中。变量清单可以被分成两个范畴:内参数和外参数。[After calibration, the list of parameters may be stored in thematab file Calib_Results by clicking on Save. Thelist of variables may be separated into two categories: Intrinsicparameters and extrinsic parameters.]
内参数(摄像机模型)[Intrinsicparameters (camera model):]
内部摄像机模型非常类似于H和S在芬兰Oulu大学使用的模型。可访问他们的网上标定页以及出版物页。我们具体推荐他们的VPR'97论文:一种带有隐含图像校正的四部摄像机标定法。[Theinternal camera model is very similar to that used by Heikkil? and Silven at the University of Oulu in Finland. Visittheir online calibrationpage, and their publication page. Wespecifically recommend their CVPR'97 paper: A Four-step Camera Calibration Procedure with Implicit ImageCorrection.]
内部参数列表[The list of internalparameters:]
焦距:摄像机光心与主点之间的距离称为焦距,它以像素为单位储存在2*1矢量fc中。[Focallength: The focal length in pixels is stored in the 2x1vector fc.]
主点:摄像机光轴与图像平面的交点,即图像中心被称为主点,其坐标(u0,v0)被保存在2*1矢量cc中。[Principalpoint: The principal point coordinates are stored in the2x1 vector cc.]
偏态系数:偏态系数定义x和y像素轴之间的夹角,被保存在标量alpha_c中。[Skewcoefficient: The skew coefficient defining the anglebetween the x and y pixel axes is stored in the scalaralpha_c.]
畸变:图像畸变系数被保存在5*1矢量kc中。[Distortions:The image distortion coefficients (radial and tangentialdistortions) are stored in the 5x1 vector kc.]
内部参数的定义[Definition of the intrinsicparameters:]
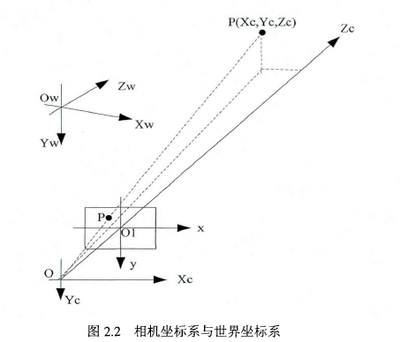
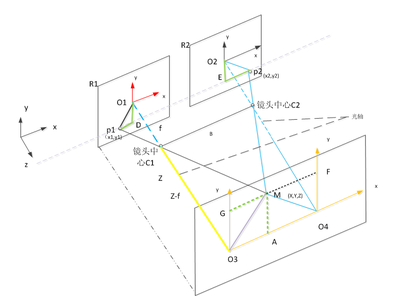
假设P是摄像机参考帧坐标矢量XXc =[Xc;Yc;Zc]空间中的一个点 [LetP be a point in space of coordinate vector XXc= [Xc;Yc;Zc] in the camerareference frame.]
现在我们按照内参数(fc,cc,alphac,kc)把该点投影在图像平面上[Let us project now that pointon the image plane according to the intrinsic parameters(fc,cc,alpha_c,kc).]
假设xn是归一化的针孔图像投影:[Let xn be the normalized(pinhole) image projection:]
Let r2 = x2 + y2.
考虑到透镜畸变,新的归一化点坐标xd被定义如下:[After including lens distortion, the newnormalized point coordinate xd is defined asfollows:]
其中dx是切向畸变矢量:[where dx is the tangential distortionvector:]
Therefore, the 5-vector kc contains both radial andtangential distortion coefficients (observe that the coefficient of6th order radial distortion term is the fifth entry ofthe vector kc).
It is worth noticing that this distortion model was firstintroduced by Brown in 1966 and called "Plumb Bob" model (radialpolynomial + "thin prism" ). The tangential distortion is due to"decentering", or imperfect centering of the lens components andother manufacturing defects in a compound lens. For more details,refer to Brown's original publications listed in the referencepage.
Once distortion is applied, the final pixel coordinatesx_pixel = [xp;yp] of the projection ofP on the image plane is:
Therefore, the pixel coordinate vector x_pixel and thenormalized (distorted) coordinate vector xd arerelated to each other through the linear equation:
where KK is known as the camera matrix, and defined asfollows:
In matlab, this matrix is stored in the variable KK aftercalibration. Observe that fc(1) and fc(2) are thefocal distance (a unique value in mm) expressed in units ofhorizontal and vertical pixels. Both components of the vectorfc are usually very similar. The ratio fc(2)/fc(1),often called "aspect ratio", is different from 1 if the pixel inthe CCD array are not square. Therefore, the camera model naturallyhandles non-square pixels. In addition, the coefficientalpha_c encodes the angle between the x and y sensor axes.Consequently, pixels are even allowed to be non-rectangular. Someauthors refer to that type of model as "affine distortion"model.
In addition to computing estimates for the intrinsic parametersfc, cc, kc and alpha_c, the toolboxalso returns estimates of the uncertainties on those parameters.The matlab variables containing those uncertainties arefc_error, cc_error, kc_error,alpha_c_error. For information, those vectors areapproximately three times the standard deviations of the errors ofestimation.
Here is an example of output of the toolbox afteroptimization:
In this case fc = [657.30254 ; 657.74391] and fc_error =[0.28487 ; 0.28937], cc = [302.71656 ; 242.33386],cc_error = [0.59115 ; 0.55710], ...
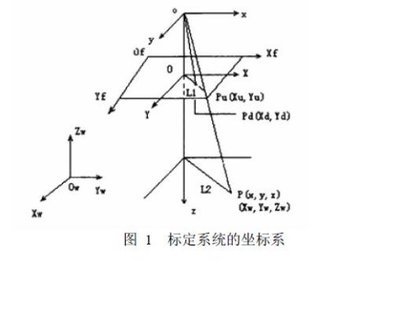
ImportantConvention: Pixel coordinates are defined such that[0;0] is the center of the upper left pixel of the image. Asa result, [nx-1;0] is center of the upper right cornerpixel, [0;ny-1] is the center of the lower left corner pixeland [nx-1;ny-1] is the center of the lower right cornerpixel where nx and ny are the width and height of theimage (for the images of the first example, nx=640 andny=480). One matlab function provided in the toolboxcomputes that direct pixel projection map. This function isproject_points2.m. This function takes in the 3D coordinatesof a set of points in space (in world reference frame or camerareference frame) and the intrinsic camera parameters(fc,cc,kc,alpha_c), and returns thepixel projections of the points on the image plane. See theinformation given in the function.
The inverse mapping:
The inverse problem of computing the normalized image projectionvector xn from the pixel coordinatex_pixel is very useful in most machine vision applications.However, because of the high degree distortion model, there existsno general algebraic expression for this inverse map (also callednormalization). In the toolbox however, a numerical implementationof inverse mapping is provided in the form of a function:normalize.m. Here is the way the function should be called:xn = normalize(x_pixel,fc,cc,kc,alpha_c). In thatsyntax, x_pixel and xn may consist of morethan one point coordinates. For an example of call, see the matlabfunction compute_extrinsic_init.m.
Reduced camera models:
Currently manufactured cameras do not always justify this verygeneral optical model. For example, it now customary to assumerectangular pixels, and thus assume zero skew (alpha_c=0).It is in fact a default setting of the toolbox (the skewcoefficient not being estimated). Furthermore, the very generic(6th order radial + tangential) distortion model is often notconsidered completely. For standard field of views (non wide-anglecameras), it is often not necessary (and not recommended) to pushthe radial component of distortion model beyond the 4th order (i.e.keeping kc(5)=0). This is also a default setting of thetoolbox. In addition, the tangential component of distortion canoften be discarded (justified by the fact that most lensescurrently manufactured do not have imperfection in centering). The4th order symmetric radial distortion with no tangential component(the last three component of kc are set to zero) is actuallythe distortion model used by Zhang.Another very common distortion model for good optical systems ornarrow field of view lenses is the second order symmetric radialdistortion model. In that model, only the first component of thevector kc is estimated, while the other four are set tozero. This model is also commonly used when a few images are usedfor calibration (too little data to estimate a more complex model).Aside from distortions and skew, other model reductions arepossible. For example, when only a few images are used forcalibration (e.g. one, two or three images) the principal pointcc is often very difficult to estimate reliably . It isknown to be one of the most difficult part of the nativeperspective projection model to estimate (ignoring lensdistortions). If this is the case, it is sometimes better (andrecommended) to set the principal point at the center of the image(cc = [(nx-1)/2;(ny-1)/2]) and not estimate it further.Finally, in few rare instances, it may be necessary to reject theaspect ratio fc(2)/fc(1) from the estimation. Although thisfinal model reduction step is possible with the toolbox, it isgenerally not recommended as the aspect ratio is often 'easy' toestimate very reliably. For more information on how to performmodel selection with the toolbox, visit the page describing the first calibration example
 爱华网
爱华网