在连续时间信号与系统中,信号一般用连续变量时间t 的函数表示,系统用微分方程描述,其频域分析方法是拉普拉斯变换和傅立叶变换。在时域离散信号与系统中,信号用序列表示,其自变量仅取整数,非整数时无定义,系统则用差分方程描述,频域分析方法是Z变换和序列傅立叶变换法。
Z变换在离散时间系统中的作用就如同拉普拉斯变换在连续时间系统中的作用一样,它把描述离散系统的差分方程转化为简单的代数方程,使其求解大大简化。因此,对求解离散时间系统而言,Z变换是一个极重要的数学工具。
2.2 序列的傅立叶变换(离散时间傅立叶变换)
一、序列傅立叶变换:
正变换:DTFT[x(n)]= (2.2.1)
反变换:DTFT-1
式(2.2.1)级数收敛条件为
| |= (2.2.2)
上式称为x(n)绝对可和。这也是DTFT存在的充分必要条件。当遇到一些绝对不可和的序列,例如周期序列,其DTFT可用冲激函数的形式表示出来。
二、序列傅立叶变换的基本性质:
1、 DTFT的周期性
, 是频率w的周期函数,周期为2p。
∵ = 。
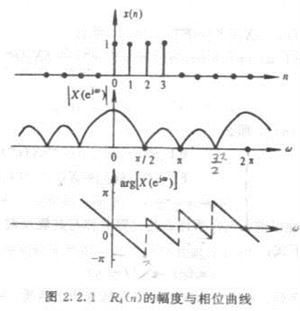
问题1:设x(n)=RN(n),求x(n)的DTFT。
= =
= =
设N为4,画出幅度与相位曲线。
2、 线性
设 =DTFT[x1(n)], =DTFT[x2(n)],
则:DTFT[a x1(n)+b x2(n)]
= = a +b
3、 序列的移位和频移
设 = DTFT[x(n)],
则:DTFT[x(n-n0)] =
=
DTFT[ x(n)] =
= =
4、 DTFT的对称性
共轭对称序列的定义:设序列 满足下式
则称 为共轭对称序列。
共轭对称序列的性质:
共轭对称序列的实部是偶函数,虚部是奇函数
证明: = +j (实部加虚部)
∵
∴ +j = -j
∴ = (偶函数)
∴ =- (奇函数)
一般情况下,共轭对称序列用 表示:
共轭反对称序列的定义:设序列 满足下式
则称 为共轭反对称序列。
共轭反对称序列的性质:
共轭反对称序列的实部是奇函数,虚部是偶函数
证明: = +j (实部加虚部)
∵
∴ +j = +j
∴ = (奇函数)
∴ = (偶函数)
一般情况下,用 来表示
一个序列可用共轭对称序列 与共轭反对称序列 之和表示。即:
x(n)= + (2.2.16)
问题1: =?
= +
= -
∴ = - (2.2.17)
= ( + )
= ( - )
对于频域函数 ,也可分解成共轭对称分量和共轭反对称分量之和:
式中, 是共轭对称分量, 是共轭反对称分量,它们满足:
= , =
且:
:共轭对称分量,它的实部是偶函数,虚部是奇函数; :共轭反对称分量,它的实部是奇函数,虚部是偶函数。
下面研究DTFT的对称性,按下面两部分进行分析
a) 将序列x(n)分成实部与虚部,即:
= +j ( 、 都是实数序列)
则:
式中: =DTFT[ ]= ,
=DTFT[j ]=j 。
结论:序列分成实部与虚部两部分,实部对应于 中的 ,虚部和j一起对应于 中的 。
b) 将序列分成共轭对称部分 和共轭反对称部分 ,x(n)= +
∵ = ( + )
= ( - )
将上面两式分别进行DTFT,得到:
DTFT[ ]= ( + )=Re[ ]=
DTFT[ ]= ( )=jIm[ ]=j
∴ = +j
x(n)= +
结论:序列的共轭对称部分 对应于 的实部 ,而序列的共轭反对称部分 对应于 的虚部加j。
应用:利用DTFT的对称性讨论当h(n)是实序列时,其DTFT的特性。
∵h(n)是实序列,所以它所对应的DTFT: = ,具有共轭对称性, 的实部偶对称,虚部奇对称。
5、 时域卷积定理
设 y(n)=x(n)*h(n)
则: = × = (2.2.32)
证明:y(n)= x(n)*h(n)=
=DTFT[y(n)]
= =
=
=
=
6、 频域卷积定理
设y(n) = x(n) h(n)
则 = * =
=
证明: = =
=
=
=
= *
7、 Parseval(帕斯维尔)(帕塞瓦尔)定理
= (2.2.34)
证明:
= =
=
=
=
2.5 Z变换的定义与收敛域
一、 Z变换的定义
若序列为x(n),则幂级数
(2.5.1)
称为序列x(n)的Z变换,也称为双边Z变换。式中z为复变量,它所在的复平面称为z平面。亦可将x(n)的Z变换表示为
ZT[x(n)] = X(z)
二、Z变换的收敛域
我们知道, 是一幂级数,只有收敛时Z变换才有意义。X(z)收敛的条件是:
(2.5.3)
X(z)能够收敛的z取值集合称为X(z)的收敛域。
一般收敛域用环状域表示。即:
∴Z变换的公式
(2.5.1)
常见的Z变换是一个有理函数,表示为:
分子多项式 的根是 的零点,分母多项式 的根是 的极点。在极点处Z变换不存在。因此收敛域中没有极点,收敛域总是用极点限定其边界。
1、 有限长序列Z变换的收敛域
有限长序列是指在有限区间n1≤n≤n2之间序列具有非零的有限值,在此区间外,序列值皆为零。有限长序列Z变换为 ,所以收敛域为
0<|z|<∞。
如n1≥0,收敛域为0<|z|≤∞。
如n2≤0,收敛域为0≤|z|<∞。
2、 右边序列Z变换的收敛域
右边序列是指在n≥n1时,x(n)有值,在n<n1时, x(n)=0。其Z变换为
此式右端第一项为有限长序列的Z变换,它的收敛域为0≤|z|<∞,而第二项是z的负幂级数,它的收敛域为 。综合此两项,只有两项都收敛时级数才收敛。所以右边序列Z变换的收敛域为 。
因果序列是最重要的一种右边序列,即n1=0的右边序列。收敛域为 (也可以写成 ),所以,|z|=∞处Z变换收敛是因果序列的特征。
3、 左边序列Z变换的收敛域
左边序列是指在n≤n2时,x(n)有值,n>n2时,x(n)=0。其Z变换为
此式第二项是有限长序列的Z变换,收敛域为0<|z|≤∞,第一项是正幂级数,收敛域为0≤|z|<Rx+。综合此两项,只有两项都收敛时级数才收敛,所以左边序列Z变换的收敛域为0<|z|<Rx+。
4、 双边序列Z变换的收敛域
这类序列是指n为任意值时x(n)皆有值的序列。 双边序列的收敛域为
问题1:求序列x(n)= RN(n)的Z变换及收敛域,并画出收敛域。
解:X(z)= = 。因为这是有限长序列,所以收敛域为0<|z|≤∞。
思考:RN(n)的DTFT存在吗?
问题2:x(n)=anu(n),求其Z变换及收敛域,并画出收敛域。
解:这是右边序列,且是因果序列,其Z变换为X(z)= 。收敛域为 (或写成 )
思考:anu(n)的DTFT存在吗?
问题3:x(n)=-anu(-n-1),求其Z变换及收敛域,并画出收敛域。
解:这是一个左边序列。其Z变换
 爱华网
爱华网