不是为了看似高级,而是因为统计学有连续复合收益率(Continuously Compounded Return)。
1. 记 t-1 时刻,你拥有的金额是 P_(t-1);在 t 时刻,你拥有的金额为 P_(t),则你的单期简单收益率(One-period Simple Return) R_t 可由下式定义:
2. 把 t-1 到 t 时刻等分成 n 份,假设每份的收益率都是一样的,也就是 r_t / n, 那么一共 n 期,上式变成这样:
取n→∞,那么该段时间就可看成连续的了,于是有
3. 由于1和2里面结果要相等,那么都取个自然对数,有
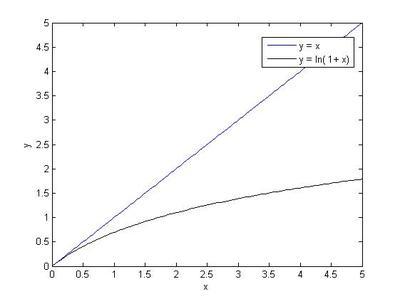
4. 如果有 k 期,那么连续复合收益率
连续符合收益率可直接线性叠加!而普通收益率得指数关系推导半天。
如果把各期的值先取对数,连续复合收益率可以直接想减得出,由连续符合收益率反推单期简单收益率和多期简单收益率就很好办了。而要是直接算简单收益率的话,那些指数会把人吓爬的。
以一个物理人的角度,最后一定要明白连续复合收益率的含义:
假设单期由无穷多收益相同的 n 个小期构成(收益率x),这些无穷多小期的总金额分别是(1+x)、(1+x)2、(1+x)3……
连续复合收益率,就是把 x 的总影响算出来,然后平均分配到 n 个小期中。那么显然可以得出,每小期的收益率最后的效果“叠加”起来,要等于单期简单收益率的。由于“叠加”实际上是连乘,那么 x = r_t / n 一定要比 R_t 要小,才能让 R_t 这个一次相乘的结果,与 n 次“叠加”的结果匹配。
验证上面的猜测:
显然,连续复合收益率比简单收益率要小!
参考文献:Analysis of FINANCIAL TIME SERIES, 3rd Edition, Ruey S. Tsay
【朱晨鸣的回答(1票)】
也不总是需要取对数,一般而言,价格(比如股价)满足对数正态分布,因为价格大于零;而收益率满足正态分布,收益率可正可负。
补充一点,在实践中,即便是处理价格类数据,也常常不取对数,而是直接计算持有期收益率(holding period yield).
【谢平凡的回答(0票)】
就一句话:加法简单还是乘法简单?
【迷锁的回答(0票)】
很少要对数化。
对数化只是个普通的数学工具,有用就用,没用就扔一边。
原文地址:知乎
 爱华网
爱华网