一、基本概念
尽管瑞利和莱斯分布确实能够在很多情况下对信号通过衰落信道后的包络进行很好的建模,然而,在实际的无线环境测试中,发现Nakagami分布提供了更好的与实际测试的匹配度[Naka60][Walter91]。与莱斯分布比较,Nakagami分布并不需要假设直射条件。
[Naka60] NakagamiM.Them-distribution. Ageneral formula of intensity distribution of rapidfading. In: HoffmanWG,editor. Statistical methods in radio wave propagation. Oxford:Pergamon; 1960.
[Walter91]Walter R. Braun, Member, IEEE,and Ulrich Dersch “A Physical Mobile Radio ChannelModel”, IEEETRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 40, NO. 2, MAY1991
(遗憾的是,本人没有能够检索到[Naka60]的这一原始文献,幸运的是文献[Walter91]大致给出了Nakagami的最初分析过程。)
在Nakagami衰落下,接收信号包络r的概率密度函数,也称为m分布,表示为:
Gamma()表示Gamma函数,μ和ω为Nakagami分布的两个重要参数,其中ω为平均功率,而μ参数(μ>=1/2),定义为”形状因子(shape fator,or shape figure)”,表示衰落的严重程度。
均值:E(r)=Gamma(μ+1/2)/Gamma(μ)*(ω/μ)^(1/2)
mean
方差:Var(r)=ω*(1-1/μ*(Gamma(μ+1/2)/Gamma(μ))^2)
Variance
(参考http://en.wikipedia.org/wiki/Nakagami-m_distribution)
在Nakagami分布下,信号的功率R服从Gamma分布:
p(R)=μ^μ*R^(μ-1)/(Re^μ*Gamma(μ))*exp(-μ*R/Re)
这里Re为平均功率。
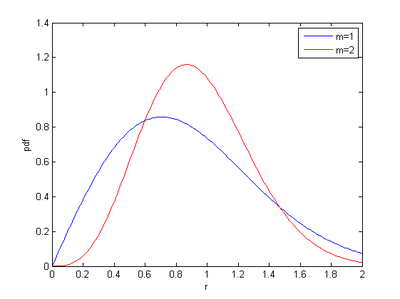
当μ=1,p(r)=1/ω*exp(-r^2/ω),发现正好是瑞利分布;
而μ=1/2时,p(r)=2/ (ω*sqrt(pi))*exp(-r^2/(2*ω)),和高斯分布一样,但由于这里r表示幅度,其取值必须大于0,因此,称为单边高斯分布。
而当μ>1的时候,Nakagami分布可以和莱斯分布近似等效。为什么说是近似等效呢,这是因为两个分布的主体部分接近,然而尾部差别较大。由于通信中断往往发生在深度衰落中,这些往往由概率密度的尾部决定,所以不可大意。
如果我们使用matlab画出p(r)分布的曲线图,会发现μ越大,图形越陡峭,当μ->无穷,p(r)成为了Dirac冲击函数。也就是说,r以无限大的概率出现在均值点,没有衰落。
二、关于μ
为什么我们把μ称之为衰落的严重程度呢?
我们已经知道(可参考"衰落、瑞利衰落和平衰落"一文),瑞利衰落就是典型的衰落信道了,或者说是一种很严重的衰落,因为瑞利信道建模了不存在直射路径下由许多反射路径叠加的信号衰落特征),而莱斯信道由于存在直射路径,相对来说衰落不是那么严重。所以,一个疑问是:还存在比瑞利衰落还要严重的衰落吗?为了比较哪个衰落更加严重,需要引入一个衰落量(amount of fading,AF)的概念(有了量化,就好比较):
AF=var( r^2)/(E(r^2))^2
其中,E[ ]表示统计平均,而var[]表示方差。
将Nakagami分布带入此定义,会发现q=1/μ,[Simon00],也就是说瑞利信道的衰落程度为1,而单边高斯分布的衰落程度为2,显然,单边高斯分布衰落比瑞利衰落还要严重。而当μ->无穷,衰落为0,这是可以理解的。
[Simon00] M.K. Simon and M.-S. Alouni,''DigitalCommunication over Fading Channels: A Unified Approach toPerformance Analysis''. Wiley,2000.
我们已经知道,在瑞利衰落下,各种调制技术的平均BER性能曲线,在高信噪比下可以表示为[Proakis00]
P(ber) ~=Gc*r^(-1)
其中Gc为编码增益,这说明在瑞利信道下可以获得分集阶数为1的性能。
[Proakis00]J. G.Proakis,''DigitalCommunications''.McGraw-Hill, 2000.
而在Nakagami衰落下,各种调制技术的平均BER性能曲线,在高信噪比下可以表示为[Wang03]
P(ber) ~=Gc*r^(-μ)
这说明其平均BER曲线的斜率,或者称为分集增益阶数,为m。
[Wang03]Z. Wang and G. B.Giannakis, “A simple and general parameterization quantifyingperformance in fading channels,”IEEE Transactions on Communications, vol. 51, pp. 1389–1398, Aug.2003
三、物理模型
在”衰落、瑞利衰落和平衰落”一文中,我们对瑞利衰落的物理模型进行了分析。分析过程中我们进行了如下的假设:
1)接收信号由大量的反射(散射)波叠加而成;2)反射波具有大致相同的信号幅度;3)不同的发射波之间互相独立;4)每一个反射子波幅度和相位独立;5)相位分布在[0, 2*pi]之间均匀分布。
根据假设1),我们可以获得接收信号叠加后为:
r= Sigma(j=1,j=N, E(j)*exp(i*theta(j))=x+j*y
这里,Sigma(,,)表示求和公式,E(j)为第j个反射波的信号幅度,theta(j)为第j个反射波的信号相位。
如果再根据(2-5)假设,那么根据中心极限定理,可以将r建模为复高斯随机过程,x和y为不相关的高斯过程,并且有<x>=<y>=0,<xy>=0。
最后接收信号的幅度可以表达为ar=abs(r)=sqrt(x^2+y^2),服从瑞利分布。是否满足瑞利分布的关键假设是各个发射波之间彼此独立,相位和幅度独立。
文献[Walter91]认为,在一个椭球形状的封闭体中,如果收发节点位于椭球体的两个焦点上,那么发射路径之间存在强相关性,因而再不能在应用中心极限定理获得瑞利信道。这种情况可以和电离层(同温层)通信,或者高楼的城市环境有些类似。
因此,需要分析更加通用情况下的任意发射波的叠加信号分布(如下),而这是非常难的。
ar=abs( Sigma(j=1,j=N, E(j)*exp(i*theta(j)))
Nakagami采用了系列的近似方法,并且根据信号的一阶和二阶统计特性,引入了两个参数m和omega,获得了Nakagami-m分布,其本质是对更一般情况下的多个随机变量和幅度分布的一个近似。因此,我们可以合理的认为莱斯衰落和瑞利衰落是其特例。
四、应用环境
Nakagami分布的提出最初为电离层和同温层的信道快速衰落建模时,发现该分布与实测数据较为温和,后来也发现在适用于陆地移动通信信道建模。也就是说在在实际的无线环境测试中,在很多情况下,Nakagami分布提供了比瑞利和莱斯信道更好的与实际测试结果的匹配。
文献[Rub05]的实际测量表明,在900MHz的城市蜂窝移动通信环境中,μ的典型值在0.5-3.5之间,平均估计值为μ=1.56处,方差为0.34,因此在理论分析中有必要考虑μ为非整数的情况。
[Rub05]Lorenzo Rubio, Juan Reig,NarcísCardona,“Evaluation of Nakagami fadingbehaviour based on measurements in urbanscenarios“,Int. J. Electron. Commun.(AEü) 61 (2007)135–138
Nakagami分布的另外一个应用是当我们研究具有m路同分布瑞利支路的MRC分集合并的信噪比时,会发现合并后的信噪比服从Gamma分布,这说明其合成信号的幅度服从Nakagami-m分布。当然,这种情况下μ只限于正整数。
五、关于WeiBull分布
最近,在阅读文献的时候,意外的发现Weibull分布和Nakagami-m分布有一定的相似度。
Weibull分布的定义:
p(r)=betta/a^(betta)*r^(betta-1)*exp(-(r/a)^(betta))
这里,betta (>0)也称为形状因子(shaper factor),a(>0)称为尺度参数(scale parameter),a越大,图形伸展越长。
均值:E(r)=a*Gamma(1+1/betta)
方差:Var(r)=a^2[Gamma(1+2/betta)-Gamma(1+1/betta)^2]
betta参数决定衰落的严重程度(fading severity),当betta=2的时候,Weibull分布退化为瑞利分布,当betta<2的时候,比瑞利衰落还严重。
最近,文献[Sen08]在研究汽车通信信道的时候,发现实测数据和Weibull分布(betta<2)较为吻合。
[Sen08]I. Sen and D. W.Matolak,“Vehicle-VehicleChannel Models for the 5-GHz Band,”IEEE Trans. IntelligentTransportation Sys., vol. 9, no. 2, June 2008, pp.235–45.
 爱华网
爱华网