关键词: 哈夫曼树; 三叉哈夫曼树; K叉哈夫曼树;哈夫曼编码
中图分类号:TP312 文献标志码:A文章编号:1006-8228(2013)09-41-02
1 二叉哈夫曼树[1-2]的构造算法
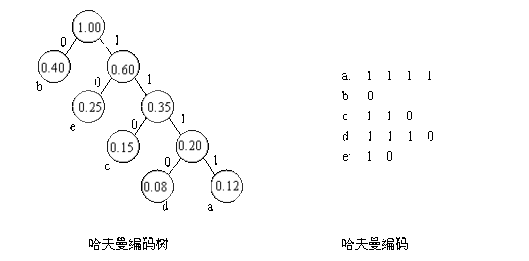
对于给定的数据序列,要生成带权路径长度最小的二叉树,应让权值越大的叶结点越靠近树根,权值越小的叶结点越远离树根。哈夫曼最早给出了一个具有一般规律的算法,称之为哈夫曼算法。
⑴根据给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵二叉树的初始集合F={T1,T2,T3…,Ti,…,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。
⑵在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树的根结点的权值之和。
⑶ 在F中删除这两棵树,同时将新得到的二叉树加入到集合F中。
⑷重复⑵和⑶,直到集合F中只含有一棵树为止。这棵树便是哈夫曼树。
2 三叉哈夫曼树构造的扩展算法
与哈夫曼算法类似,可以每次取三个根结点权值最小的树作子树,构造一棵新的三叉树,算法思路如下。
⑴根据给定的n个权值{W1,W2,W3,…,Wi,…,Wn}构成n棵三叉树的初始集合F={T1,T2,T3,…,Ti…,Tn},其中每棵三叉树Ti中只有一个权值为Wi的根结点,它的左、中、右子树均为空。
⑵在F中选取三棵根结点的权值最小的树作为左、中、右子树构造一棵新的三叉树,且新得到的三叉树的根结点的权值为其左、中、右子树的根结点的权值之和。
⑶ 在F中删除这三棵树,同时将新得到的三叉树加入到集合F中。
⑷ 重复⑵和⑶,直到集合F中只含有一棵树为止[3]。
此算法由二叉哈夫曼算法扩展而来,因而将它称为三叉哈夫曼树构造的扩展算法。
3 k叉哈夫曼树的构造
设有n个信源符号,在传输过程中的概率分别是W1,W2,W3,…,Wn,将概率设为权值。k0=(n-1)mod(k-1),当k0=0时,(n-1)/(k-1)为整数,哈夫曼树中只有度为0和k的结点;当k0≠0,即(n-1)/(k-1)不为整数时,需添加k-1-k0个权值为0的结点。算法思路如下。
⑴作n棵树的集合F={T1,T2,T3,…,Ti,…,Tn},每棵树Ti只有一个权值为Wi的根结点,且均无子女。
⑵计算k0=(n-1)mod(k-1);若k0≠0,则添加k-1-k0个权值为0的结点,并作为k-1-k0棵树添加到F中,否则不用添加。
⑶在F中选k棵根结点权值最小的树作子树,构造一棵新的k叉树,其根结点的权值为所有子树根结点的权值之和,并在F中删除这k棵树,且将新得到的k叉树加入F中。
⑷重复⑶,直到F中只剩下一棵树为止。则该树即为k叉哈夫曼树。
4 用C语言[4-6]实现
4.1 存储结构
由树的孩子兄弟表示法及线索二叉树存储结构中标志域的启发,采用如下存储结构:
struct hlnode
{ float weight;
struct hlnode *llink;
struct hlnode *rlink;
int tag;
}
其结点的结构如图1所示。
[llink\&weight\&tag\&rlink\&]
图1 结点结构图
llink:指针,指向该结点的第一个孩子结点;
weight:记录该结点的权值;
tag:其取值为0,1,2,…,k-1;任一父结点,其第一个孩子结点到最后一个孩子结点的tag值按照k-1,k-2,…,2,1,0排列,这样每个结点的tag值还表示其最后一位编码的码值;
rlink:指针。
⑴当tag=0时,指向该结点的父结点,且该结点为其父结点的最后一个孩子即第k个孩子;
⑵当tag=n(n=k-1,k-2,…,2,1)时,指向该结点的下一个兄弟,且该结点为其父结点的第k-n个孩子。
可利用这种存储结构中所有叶子结点空的llink域将叶子结点按权值的升序连接成一个叶子的单链表leaf。这样在求编码时,沿着链表leaf的llink域可以迅速找到信源符号所在的叶子结点,然后再对叶子结点求编码。
4.2 算法描述[7-8]
K叉哈夫曼树的构造算法如下:
⑴ 建立一个带头结点的空链表L;
⑵ 读入n个信源符号的权值,并升序存入链表L中;
⑶计算k0=(n-1)mod(k-1);若k0≠0,则在链表L的表头结点后插入k-1-k0个权值为0的结点;
⑷取链表L中的前k个结点作子树,产生一个新的结点作其父结点,父结点的权值为这k棵子树根结点的权值之和;
⑸将子树中的叶子结点链入链表leaf中,并从链表L中删除这k棵子树;
⑹ 将新产生的父结点按升序插入链表L中;
⑺重复⑷、⑸、⑹,直到链表L中除表头结点外只剩下一个结点为止,则该结点即为k叉哈夫曼树的树根结点;
⑻ 用指针r指向链表leaf的第一个结点;
⑼将当前指针r所指结点的tag值存入数组cd[]中,整型变量sp为当前结点的码值在数组中的位置;
(10)通过rlink域找到当前结点的父结点,将其tag值存入数组cd[]中;
(11)重复(10),直到到达根结点(即父结点为空的结点)为止,此时,sp为指针r所指结点的最后一位码值在数组中的位置,按位置的逆序将数组中存放的码值全部输出,即为指针r所指结点的哈夫曼编码。
(12)将指针r后移,重复⑼、(10)、(11),直到所有叶子结点的编码皆已求出(即指针r为空)为止。
5 结束语
数据编码技术在计算机通信和信息压缩中一直占据着重要地位,依照哈夫曼树得到字符编码的算法作为通用的数据压缩方法,是大多数通用压缩程序的基础,并且往往作为压缩过程中的一个步骤。本文通过分析二叉哈夫曼树及三种三叉哈夫曼树的构造算法,提出了k叉哈夫曼树的构造算法,并得到k进制最优前缀编码。所求得的各叶子结点的代码长度虽不等,但最长不会超过分支点个数x(叶子结点的路径长度的最大值),而且k越大,平均编码长度会越短,对数据通信、信息压缩等领域有较大的促进作用,而且k可以是任何大于2的正整数,应用范围更为广阔。
参考文献:
[1]刘爱民.离散数学[M].北京邮电大学出版社,2004.
[2]方景龙,王毅刚.应用离散数学[M].人民邮电出版社,2005.
[3]严蔚敏,吴伟民.数据结构(C语言版)[M].清华大学出版社,2005.
[4]任正云.哈夫曼树及其在信息编码中的应用[J].沙洋师范高等专科学校学报,2007.5:31-32
[5]黄锦祝.用C语言实现三叉哈夫曼树[J].福建电脑,2004.3:64-65
[6]吕文志,戎丽霞.一种新的三叉哈夫曼树生成算法[J].福建电脑,2006.7:91-92
[7]朱祥正.基于k叉树的最优树[J].计算机应用研究,1998.1:39-41
[8] 王玲.树的父母—子女环存贮结构[J].四川师范大学学报,2000.6:20-21
 爱华网
爱华网


