方法一(prim算法);
普利姆(Prime)算法(只与顶点相关)
算法描述:
普利姆算法求最小生成树时候,和边数无关,只和定点的数量相关,所以适合求稠
密网的最小生成树,时间复杂度为O(n*n)。
算法过程:
1.将一个图的顶点分为两部分,一部分是最小生成树中的结点(A集合),另一部分
是未处理的结点(B集合)。
2.首先选择一个结点,将这个结点加入A中,然后,对集合A中的顶点遍历,找出A中
顶点关联的边权值最小的那个(设为v),将此顶点从B中删除,加入集合A中。
3.递归重复步骤2,直到B集合中的结点为空,结束此过程。
4.A集合中的结点就是由Prime算法得到的最小生成树的结点,依照步骤2的结点连接
这些顶点,得到的就是这个图的最小生成树。
#include <iostream>
using namespace std;
#define MAX 999999
int map[100][100],dis[100];//以节点i为终点的最小边权值;
int mark[100];
int n;
void prim()
{
int i , j , k , min , sum = 0;
for( i = 1 ; i <= n ; i++)
dis[i] = map[i][1];//因为节点1已经默认进入最小树,所以初始化应该是节点1到节点i的值;
mark[1] = 1 ;
for( i = 2 ; i <= n ; i++)
{
min = MAX;
k = i;
for( j = 2 ; j<= n ; j++)//找出最小边权值;
if(!mark[j]&& dis[j] < min)
{
min= dis[j];
k= j;
}
sum += min;//累加权值;
mark[k] = 1;//标记节点k加入生成树;
for( j = 2 ;j <= n ; j++)//更新权值;
if(map[j][k] < dis[j])
dis[j]= map[j][k];
}
printf("%dn",sum);
}
int main()
{
int i , x , y , d ;
while(scanf("%d",&n) != EOF&&n)
{
for( i = 1 ; i<= n ; i++)
{
map[i][i] = 0;
mark[i] = 0;
}
for( i = 0 ; i <n * (n - 1) / 2 ; i++)
{
scanf("%d %d%d",&x,&y,&d);
map[x][y] =map[y][x] = d;
}
prim();
}
return 0;
}
方法二(kruskal 算法)
算法过程:
1.将图各边按照权值进行排序
2.将图遍历一次,找出权值最小的边,(条件:此次找出的边不能和已加入最小生成
树集合的边构成环),若符合条件,则加入最小生成树的集合中。不符合条件则继
续遍历图,寻找下一个最小权值的边。
3.递归重复步骤1,直到找出n-1条边为止(设图有n个结点,则最小生成树的边数应
为n-1条),算法结束。得到的就是此图的最小生成树。
#include<stdio.h>
#include<stdlib.h>
typedef struct path{
int s,e,len;
} path;
int f[101];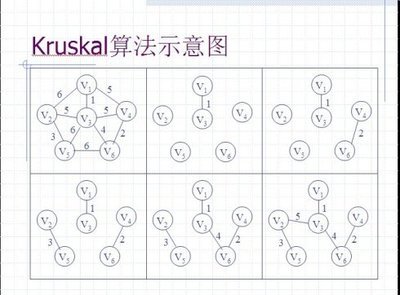
int min(int x,int y)
{
if(x<y)
return x;
return y;
}
int find(int x)
{
if(x!=f[x])
f[x]=find(f[x]);
return f[x];
}
void Union(int x,int y)
{
int xx,yy;
xx=find(x);
yy=find(y);
f[xx]=f[yy]=f[x]=f[y]=min(xx,yy);
}
int cmp(const void *a,const void *b)
{
path *c,*d;
c=(path *)a;
d=(path *)b;
returnc->len-d->len;
}
int main()
{
path p[5000];
int n,i,j,sum;
while(scanf("%d",&n),n!=0)
{
for(i=0;i<n*(n-1)/2;i++)
scanf("%d %d%d",&p[i].s,&p[i].e,&p[i].len);
qsort(p,n*(n-1)/2,sizeof(p[0]),cmp);
j=0;
for(i=1;i<=n;i++)
f[i]=i;
sum=0;
for(i=0;i<n*(n-1)/2;i++)
{
if(j==n-1)
break;
if(find(p[i].s)==find(p[i].e))
continue;
Union(p[i].s,p[i].e);
sum=sum+p[i].len;
j++;
}
printf("%dn",sum);
}
return 0;
}
 爱华网
爱华网