二维数组:
首先想到用二维数组比较容易实现,试着写了一个(只输出10行)。思路:先将两侧元素,即每一行的开始值与结束值均置为1,然后从第三行开始(一、二行全为1),除首尾两个元素外的其他元素为其左上角元素与正上方元素之和。
#include <stdio.h>
#define N10
int main()
{
int i;
int j;
inta[N][N];
for (i =0; i < N; i++)
{
a[i][0] =1;
a[i][i] =1;
}
for (i =2; i < N; i++)
for (j = 1; j < i; j++)
a[i][j] = a[i-1][j-1] + a[i-1][j];
for (i =0; i < N; i++)
{
for (j = 0; j <= i; j++)
printf("%-5d", a[i][j]);
printf("n");
}
return0;
}
那么怎样才能显示成金字塔形状呢?问题在于如何将每行前的空格数与行号结合起来,这样就可以在循环输出各行时方便地输出空格数了,观察前面所绐的金字塔形状的规律:
第1行 i = 0 空格数 30 =3 × N-3 ×0
第2行 i = 1 空格数 27 =3 × N-3 ×1
第3行 i = 2 空格数 24 =3 × N-3 ×2
......
第N行 i = i空格数3×N-3×i
按上述规律编写程序,限于屏幕显示宽度,1个数用6位宽度最多只能输出13行,再多的话看上去就不爽了:
#include <stdio.h>
#define N 13
int main()
{
int i;
int j;
inta[N][N];
for (i =0; i < N; i++)
{
a[i][0] = 1;
a[i][i] = 1;
}
for (i =2; i < N; i++)
for (j = 1; j < i; j++)
a[i][j] = a[i-1][j-1] + a[i-1][j];
for (i =0; i < N; i++)
{
for (j = 0; j < (N * 3 - 3 * i); j++)
printf(" ");
for (j = 0; j <= i; j++)
printf("%-6d", a[i][j]);
printf("n");
}
return0;
}
★ 关于每一行前面的输出的空格还有一种方法。在 [016]printf格式控制符的完整格式 一文中(第一个拾遗处)提到了一种printf的输出方式,例如定义了一个字符串ch[20],若想以宽度为6输出,一般会用printf("%6s",ch); 输出,这种方法可认为是静态的,即这个宽度不能变,有一种形式可以实现动态输出: printf("%*sn", m, ch);这里由m的值代替*位置, 即宽度*可以由变量m来确定。用上述方法可以将上面程序中的
for (j = 0; j < (N * 3 - 3 * i); j++)
printf(" ");
换成: printf("%*c", 3 * N - 3 *i, ' ');
即在每行前以c格式输出 3*N-3*i 个 ' ' (空格), 可以得到相同的结果。
一维数组:
前两天在网上看了一位仁兄用一维数组做的, 当时只保存其代码,现在找不到原帖了,那就先把人家的程序拿来分析一下吧(稍加修改):
#include <stdio.h>
void main()
{
int N =13;
int a[80] ={0};
int b[80] ={0};
int i,j;
b[1]=1;
for (i =1; i <= N; i++)
{
for (j = 1; j <= i; j++)
a[j] = b[j] + b[j-1];
for (j = 1; j <= i; j++)
{
b[j] = a[j];
printf("%-6d", b[j]);
}
printf("n");
}
}
★ 分析: 其思路是用一维数组做,实际上用的是两个一维数组a[], b[].其中a[]是保存当前行各元素的值,而b[]可以认为是一个临时数组, 它是a[]的一个备份,也就是说在每行a[]元素置数完毕后,将a[]中的内容拷贝到b[]中,因为进行下一行的运算时, a[]会被重置,而且由杨辉三角的规律知下一行要用到上一行的元素,这样在计算下一行的a[]时就可以用保存在b[]中的上一行的元素了(咋感觉这么啰嗦呢^_^)。也正因为如此,在每一行运算完之后,就要将其输出显示,下一行时a[]就是新值了。所以用这种方法最后程序结束时并没有将三角中所有元素保存下来,只是在程序运行过程中将其输出。
再看其程序的核心部分:a[j] = b[j] + b[j-1];其开始定义了数组a[80],b[80],0号元素并未使用,即每一行的元素都是从a[1]开始的。但这个0号元素是不是真的没用呢?稍加分析可知当然否,而且感觉这个0号元素用的挺巧妙,比如说到第5行时(其实与第几行没关系),输出第一个元素的语句是a[1]=b[1]+b[0], 由于b[1]为1, 这时0号元素就派上用场了,b[0]为0, 可以将每一行的第一个元素置为1,往下走有第二个元素 a[2]=b[2]+b[1];...开始按杨辉三角的规律走。同理,到最后一个元素时,a[5]=b[5]+b[4],在上一行中只有4个元素,即此时b[]中只有4个有效元素,那这个b[5]算什么呢?其实它跟那个0号元素有相同的作用,因为初始化时数组中的所有元素都置为0,所以这时的b[5]为0,由b[4]为1可得a[5]为1。这样可以将每一行的最后一个元素置为1。对于各行,此法均适用,实际上就是在满足杨辉三角两侧值均为1的规律。
#include <stdio.h>
#include <stdlib.h>
void main()
{
int i,j;
int*a;
int*b;
int N;
do
{
printf("How many lines do you want to print? ");
scanf("%d", &N);
}while(N< 0 || N > 13);
printf("n");
a = (int*) malloc((N + 1) * sizeof(int));
b = (int *)malloc((N + 1) * sizeof(int));
for (i =0; i <= N; i++)
{
a[i] = 0;
b[i] = 0;
}
b[1]=1;
for (i =1; i <= N; i++)
{
for (j = 1; j <= i; j++)
a[j] = b[j] + b[j-1];
for (j = 1; j <= (3 * N - 3 * i); j++)
printf(" ");
for (j = 1; j <= i; j++)
{
b[j] = a[j];
printf("%-6d", b[j]);
}
printf("n");
}
}
一维数组又一法:
在别人日志上看到一篇文章 (查看原文) , 是用一个一维数完成的, 其原程序有点小错误,稍加修改拿来分析一下吧:
#include <stdio.h>
#define N10
void main()
{
inta[N+1];
inti,j;
a[0] = a[1]= 1;
printf("%-5dn",1);
printf("%-5d%-5dn",a[0],a[1]);
for (i = 1;i < N - 1; i++)
{
a[i + 1] =a[i];
for (j = i; j > 0; j--)
a[j] = a[j - 1] + a[j];
for (j = 0; j < i + 2; j++)
printf("%-5d", a[j]);
printf("n");
}
}
★ 分析: 此程序是以杨辉三角的前两行为基础的,所以前两行的值已经确定, 后续行由三角的规律得到。程序中用一个一维数组a[]记录生成的值,每一行都要刷新,数组的0 号元素作用与上一个程序(两个一维数组实现)中的作用类似,叠加时生成第二个元素值,所以分配数组时要多分配一个元素,即a[N+1]。还有由于前两行已经提前输出,故用循环输出后续值时要注意条件是i < N - 1, 且i =1时输出的是第三行。按循环走上两行就能明白其原理了, 由i = 1 时开始, 此时应输出第三行的值:
i=1a[0]=1
a[1]=1
a[2]=a[1]=1
j=i=1a[1]=a[0]+a[1]=1+1=2 => j--=> j=0 => 结束
最终a[0]=1, a[1]=2, a[2] = 1;
--------------------------------------------------------------------
i=2a[0]=1
a[1]=2
a[3]=a[2]=1
j=i=2a[2]=a[1]+a[2]=1+2=3 => j--=> j=1 => 继续
j = 1a[1]=a[0]+a[1]=1+2=3 => j--=> j=0 => 结束
最终a[0]=1, a[1]=3, a[2] = 3, a[3]=1;
……
依次类推即可得到各行。 其巧妙之处在于a[i+1]=a[i]这句,将最外边的1外移了一位。
当然也可以用上个程序那样动态分配数组实现, 不再赘述。
二项式定理:
既然杨辉三角为二项式系数表,那能不能用二项式定理来编呢? 我没有思路, 看到一个帖(查看原帖) 中有人用C++写了一个, 不过怎么也看不明白其原理, 用C稍加修改,程序先放到这, 想明白了再补上:
#include <stdio.h>
void main()
{
double A, n,s, sum, m, X;
doublet;
s = 1;
sum =1;
do
{
printf("lines: ");
scanf("%lf", &X);
} while(X<= 0 || X > 13);
printf("%dn", 1);
for(A = 1; A<= (X - 1); A++)
{
printf("%-6d", 1);
for(n = 1; n <= A; n++)
{
s *= n;
m = (A - n + 1);
sum *= m;
t = sum / s;
printf("%-6d", (int)t);
}
printf("n");
}
}
二项式定理:
既然杨辉三角为二项式系数表,那能不能用二项式定理来编呢? 我没有思路, 看到一个帖(查看原帖) 中有人用C++写了一个, 不过怎么也看不明白其原理, 用C稍加修改,程序先放到这, 想明白了再补上:
#include <stdio.h>
void main()
{
double A, n,s, sum, m, X;
doublet;
s = 1;
sum =1;
do
{
printf("lines: ");
scanf("%lf", &X);
} while(X<= 0 || X > 13);
printf("%dn", 1);
for(A = 1; A<= (X - 1); A++)
{
printf("%-6d", 1);
for(n = 1; n <= A; n++)
{
s *= n;
m = (A - n + 1);
sum *= m;
t = sum / s;
printf("%-6d", (int)t);
}
printf("n");
}
}
递推公式法:
还是在这个帖中 (查看该帖) 还有一种方法, 不知应该叫什么, 自己分析了一下, 算是看懂了,就先叫它"递推公式法吧" , 稍加改动,拿过来分析一下:
#include "stdio.h"
void main()
{
intc;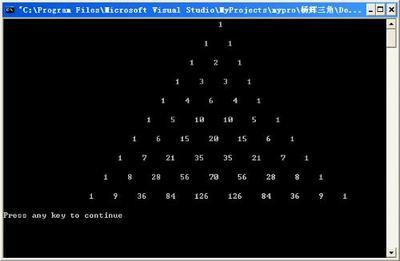
intn;
int i,j;
do
{
printf("Input n=");
scanf("%d",&n);
} while(n<= 0 || n > 13);
for(i =0; i < n; i++)
{
for(j = 0; j < n - i; j++)
printf("%3c", ' ');
c=1;
for(j = 0; j <= i; j++)
{
printf("%-3d", c);
printf("%-3c", ' ');
c = c * (i - j) / (j + 1);
}
printf("n");
}
}
★ 分析: 此方法每个元素都是在循环中由控制变量i, j 及公式 c=c*(i-j)/(j+1); 生成的, c即元素的值,每行输出前都将c的值置1, 这样解决了将每行第一个值置1的问题, 接着由递推公式及行值i、列值j依次得出后面的元素。过程嘛说出来反而啰嗦,其实按循环走上那么三四行就能明白其含义了。比如生成第四行时,i 为3,走一遍:
j = 0 时: 输出 c = 1--> 递推 c = 1 * (3 - 0) / (0 + 1) = 3
j = 1 时: 输出 c = 3--> 递推 c = 3 * (3 - 1) / (1 + 1) = 3
j = 2 时: 输出 c = 3--> 递推 c = 3 * (3 - 2) / (2 + 1) = 1
j = 3 时: 输出 c = 1--> 结束
不知这个规律是发帖这位仁兄总结出来的, 还是它本身就是二项式系数的一种内在形式。总之感觉很牛×。
另外此程序中每行前输出空格的方法和前面提到的也不太一样,它是用位宽控制输出一个空格做到的,当然和前面的方法通用。即可以将
for(j = 0; j < n - i;j++)for (j = 0; j < (n * 3 - 3 * i); j++)
printf("%3c", '');改为==>printf("");
或 ==> printf("%*c", 3 * n - 3 * i,' ');
 爱华网
爱华网