我们用Y表示某经济系统的产出量,L表示该经济系统的劳动投入量,K表示该经济系统的资本投入量,A表示该经济系统的技术水平,则经由柯布道格拉斯生产函数,我们有:
产出的增量(△Y)=资本的边际产量×资本投入的增量(△K)+劳动的边际产量×劳动投入的增量(△L)+技术水平的边际产量×技术进步的增量(△A)
在上式两边同除以产量Y,并在等号右边第一项的分子分母同乘以K、第二项的分子分母同乘以L,从而有:
经济增长率=资本投入的产出弹性×资本投入的增长率+劳动投入的产出弹性×劳动投入的增长率+技术进步率。
根据经济理论,当生产要素市场实现均衡的时候,生产要素的价格应该等于它的边际产量,因此,“资本投入的产出弹性”和“劳动投入的产出弹性”分别相当于资本和劳动这两种生产要素的所有者在国民收入中所享有的份额。
例如,具体地假定某经济系统的(C-D)生产函数为Y=A(K^a)(L^(1-a)),其中,a为正参数(资本投入的产出弹性或资本生产要素在国民收入中所享有的份额)。显然,这是一个线性齐次生产函数,这意味着我们隐含地假定该经济系统正处于规模报酬不变的状态。
我们对这个具体形式的生产函数先求自然对数、再求微分,最终可得:
人均产出的增长率=人均资本存量的增长率×a+技术进步率。
可见,人均经济增长率的高低取决于人均资本存量的增长率和技术进步的速度。
现在假定经济系统已经处于均衡状态,即投资需求(I)=储蓄(S)。再假定储蓄函数为 S=sY,并且假定不存在设备更新问题,则有S=I=△K=sY。
如果再假定技术水平不变,则根据“经济增长率=资本投入的产出弹性×资本投入的增长率+劳动投入的产出弹性×劳动投入的增长率+科学技术进步率”,有:
经济增长率=a×资本投入的增长率+(1-a)×劳动投入的增长率。
进而有:
经济增长率=a(△K/K)+(1-a)×劳动投入的增长率;
经济增长率=a(sY/K)+(1-a)×劳动投入的增长率。
再考虑到资本投入的产出弹性a=(△Y/Y)/(△K/K),因而有:
经济增长率=s(△Y/△K)+(1-a)×劳动投入的增长率。
上式中,(△Y/△K)相当于哈罗德模型中的资本-产出比(v)的倒数。
可见,若再假定劳动投入的数量既定,则有 :
经济增长率=s(△Y/△K)=s/v。
这一结果与哈罗德-多马模型的结论一致。
不过,新古典经济增长模型认为,产量与资本投入之间的技术关系,进而劳动投入的数量不会固定不变。这样一来,如果“经济增长率>资本投入的增长率”,即产量的增长速度快于资本存量的增长速度,则说明资本的生产效率较高,这会刺激企业以资本替代劳动。这一过程的结果会导致资本的边际产量递减,伴随着劳动投入增长率的下降,最终经济增长的速度会趋于减缓。
反之,如果“经济增长率<资本投入的增长率”,即产量的增长速度低于资本存量的增长速度,则说明资本的生产效率较低,这会刺激企业以劳动替代资本。这一过程的结果会导致资本的边际产量随着劳动投入增长率的提高而递增,最终经济增长的速度会趋于加速。
可见,只有在“经济增长率=资本投入的增长率”的时候,企业才不存在调整资本存量的意愿,从而劳动投入也会固定,从而生产要素投入的比例也就稳定下来。
因此,当经济系统实现均衡的时候,经济增长率将等于资本存量的增长率。由式“经济增长率=a×资本投入的增长率+(1-a)×劳动投入的增长率”不难看出,均衡经济增长率不仅等于这时的资本存量增长率,并且还等于劳动人口的增长率。也就是说,经济系统会自行趋于充分就业均衡。
现在我们换个方式重新阐述一遍新古典经济增长模型的上述逻辑。为增加一点新信息量,我们将考虑存在设备更新的情景。
当资本存量为K的时候,我们假定折旧率为0<z<1,则资本存量的变动量为△K=I-zK。我们仍然不考虑政府与对外贸易的影响,则当经济系统实现均衡的时候,由S=I=sY,有:
△K=sY-zK
在上式两边同除以L,并令人均国民收入为y,人均资本存量为k,劳动投入增长率为n,我们有:
(△K)/L=s(Y/L)-z(K/L)
(△K)/L=sy-zk(1)
另外,由于k=K/L,进而有(△k/k)=(△K/K)-(△L/L),所以有:
△K=(△k/k)×K+nK
在上式两边同除以L,得:
(△K)/L=(△k)+nk(2)
综合考虑式(1)和(2),最终有:
(△k)+nk=sy-zk
sy=(△k)+(z+n)k
可见,当经济系统实现均衡的时候,人均储蓄有两个去处:一方面被作为设备更新改造以及为新增劳动力配备资本设施的资金来源,以便能够维持既有的人均资本存量((z+n)k);另一方面被作为提高人均资本存量的资金来源(△k)。
例如,假若sy>(z+n)k,则说明可贷资金充裕,除了维持人均既有资本存量的需要以外还有剩余,于是企业会加大资本设备的投入,人均资本存量随之提高;而假若sy<(z+n)k,则说明企业更新改造资金匮乏,难以维持简单再生产,人均资本存量随之下降。只有在sy=(z+n)k的时候,企业正好维持简单再生产,人均资本存量保持不变(即△k=0),经济系统随之实现稳定。
显然,当sy=(z+n)k的时候,由于△k=0,所以根据人均资本存量的定义,必有“经济增长率=资本投入增长率”。再考虑到劳动力增长率既定为n,因此,由k=K/L的定义,当△k=0的时候,必有△K/K=n。因此,当国民经济系统实现均衡的时候,必有:
经济增长率=资本投入增长率=人口增长率。
可见,在不考虑技术进步的前提下,当整个经济系统实现均衡的时候,人均经济增长率以及人均资本投入增长率必定等于零。当然,这个时候的经济总量增长率并不等于零。实际上,这个时候的均衡经济增长率必定等于资本投入增长率以及劳动投入增长率。
而且我们发现,在sy>(z+n)k的时候,伴随着人均资本拥有量的提高,人均经济增长率呈递增的趋势。假若人口增长率保持不变,这就意味着,经济总量的增长率将高于均衡增长率(即人口增长率)。反过来,在sy<(z+n)k的时候,伴随着人均资本拥有量的下降,人均经济增长率呈递减的趋势。假若人口增长率保持不变,这就意味着,经济总量的增长率势必低于均衡增长率(即人口增长率)。由此,我们就能明白,为什么像中国这样的发展中国家,其经济增长率会明显地高于发达国家了。
按此逻辑,人均资本越低的经济体,其增长率应当越高,最终人均实际GDP将趋于一致。按此结论,穷国的人均实际GDP增长应当比富国更快,并最终赶上富国,即实现所谓的“赶超”。这叫绝对收敛。
另外还存在相对收敛,即一个经济体距离其自身经济的稳定状态越远,其增长就越快。也就是从长期来看,在其他条件不变的情况下,一个经济体存在一个稳定的状态,若该经济体距离此稳定状态较远,则会以较快的速度增长,但随着趋近此稳定状态,增长速度也会逐渐变慢。同时,不同的经济体具有人均实际GDP不同的稳定状态,因此在一定的条件下,穷国可能永远赶不上富国。
在上述分析中,我们假定储蓄率保持不变。现在我们放松这个假定,例如假定储蓄率提高,则会提高人均资本拥有量,从而提高人均经济增长率。不过,在这一更高的储蓄率假定下,依据上述逻辑,最终国民经济仍会重新实现均衡,也即人均经济增长率仍会重新为零,经济总量的增长率仍会重新回落至人口增长率的水平。当然,在这个新的均衡状态下,经济的总量将较储蓄率变动之前要明显提高。
现在再放松人口增长率保持不变的假定。例如假定人口增长率提高,即n增大,则会降低人均资本拥有量,从而压低人均经济增长率。不过,最终国民经济仍会重新实现均衡,也即人均经济增长率会重新为零。这个时候,经济总量的增长率仍将达到人口增长率的水平,而经济总量较人口增长率变动之前要明显提高。可见,两个其他条件完全相同的国家相比较,人口增长率较高的国家应该拥有较高的稳态经济总量增长率,但人均国民收入较低。
发展中国家的人口增长率通常较高,所以这些国家的较高经济增长率并不难理解。就此说来,由于印度的人口增长率高于中国,所以仅就这个因素来说,印度的经济增长率超过中国实乃必然。
经济增长的终极目的是提高该经济系统内部每一个居民的福利水平。如果假定福利仅源于消费的过程,则消费与投资之间存在辩证统一的关系。也就是说,它们之间最终应该是一致的,因为无论是消费还是投资,其目的都是为了实现居民整个人生期间效用的最大化;不过,它们之间又具有矛盾性,这是因为当前消费的变动会影响储蓄,而储蓄的变动会影响投资,进而影响人均资本存量,最终影响未来的收入和消费。
如果将经济增长的目标具体化为促使稳态人均消费的最大化,那么在技术水平和人口增长率固定不变的前提下,最优的稳态人均资本存量是多少呢?对此,费尔普斯(1961)的回答是:稳态人均资本存量的选择应使资本的边际产量等于劳动增长率。这一结论被称为黄金分割律。
黄金分割律的证明并不困难。为简便起见,我们不考虑折旧,并继续假定不存在技术进步的问题,则由sy=△k+(z+n)k可知,当经济系统处于稳定状态的时候(这时△k=0),必有sy=nk。
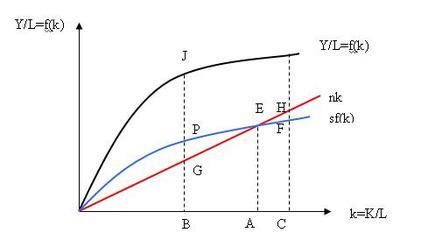
再假定该经济系统的生产函数为y=f(k),则该经济系统的稳态人均消费量(用符号c表示)为:
c=y-sy=f(k)-nk。
为求得人均消费(c)最大化的必要条件,对上式中的c关于k求导数,并令之为零,有:
df(k)/dk=n
再考虑到生产函数的二次导数具有小于零的性质,则满足df(k)/dk=n的人均资本k的确能够产生最高的人均消费水平。
新古典经济增长理论从二世纪六十年代到八十年代中期一直在西方经济增长理论研究中占据主导地位。新古典经济增长理论假定总量生产函数具有规模报酬不变的性质,即投入增加一倍,产出也增加一倍。而且新古典经济增长理论认为,不同国家的经济增长具有趋同性,也就是说,有着相同技术水平及人口增长率的国家最终都会趋于相同的稳态增长率。这些假定和结论与战后各国几十年经济增长的现实存在巨大的差异。
新古典经济增长理论暗示:稳态增长率是外生的,因为该理论并没有解释劳动力增长率和技术进步率的内在机制,而只是笼统地将其视作外生变量。实际上,增长率的外生化是新古典经济增长理论所有缺陷的集中体现,因为人口增长率的变动和科学技术水平的变化对于经济增长的影响已经是不争的事实,许多国家的政府正在着手通过制定能动的人口政策和科技政策来调控经济的增长,但是新古典经济增长理论无法给出相应的解释及政策建议。
正是在这样的反思背景下,自二十世纪八十年代开始,经济增长理论获得了明显的发展,逐步形成了所谓的“新经济增长理论”。
新经济增长理论设定宏观经济具有规模报酬递增的性质,并且技术进步具有内生性,凭以说明经济增长的原因和路径,并解释各国经济增长率存在巨大差异的原因。新经济增长理论的最终成果是将经济增长内生化,由此,新经济增长理论又被称为内生经济增长理论。(转载)
 爱华网
爱华网


