计算部分
要想提高计算能力,首先要学好各种运算的法则、运算定律及性质,这是计算的基础。
其次是要多做练习。这里说的“多”是高质量的“多”,不单是数量上的“多”。多做题,多见题才能见多识广、熟能生巧,坚持不懈就能提高计算能力。
再次是养成速算、巧算的习惯。能速算、巧算是一个学生能综合运用计算知识、计算能力强的突出表现。比如计算855÷45。你见到这个题就应该想到:900÷45=20,而 855比 900少45,那么855÷45的商应比900÷45的商小1,应是19。
要想提高计算能力,还要掌握一些简算、巧算的方法,这要有老师的指导。看看下面的例题,是一定会得到启发的。
分析与解在进行四则运算时,应该注意运用加法、乘法的运算定律,减法、除法的运算性质,以便使某些运算简便。本题就是运用乘法分配律及减法性质使运算简便的。
例2 计算 9999×2222+3333×3334
分析与解 利用乘法的结合律和分配律可以使运算简便。
9999×2222+3333×3334
=3333×(3×2222)+3333×3334
=3333×6666+3333×3334
=3333×(6666+3334)
=3333×10000
=33330000
分析与解 将分子部分变形,再利用除法性质可以使运算简便。
分析与解 在计算时,利用除法性质可以使运算简便。
分析与解 这道分数乘、除法计算题中,各分数的分子、分母的数都很大,为了便于计算时进行约分,应该先将各分数的分子、分母分别分解质因数,这样计算比较简便。
分析与解 通过观察发现,原算式是求七个分数相加的和,而这七个分
由此得出原算式
分析与解观察题中给出的数据特点,应该将小括号去掉,然后适当分组,这样可使运算简便。
分析与解 观察这些分数的分母,都是连续自然数的和,我们可以先求出分母来,再进行拆项,简算。
分析与解 我们知道
例12 计算 1×2+2×3+3×4+……+10×11
分析与解
将这10个等式左、右两边分别相加,可以得到
例13 计算1×3+2×4+3×5+4×6+……+50×52
分析与解 我们知道
1×3=1×3-1+1=1×(3-1)+1=1×2+1
2×4=2×4-2+2=2×(4-1)+2==2×3+2
3×5=3×5-3+3=3×(5-1)+3=3×4+3
4×6=4×6-4+4=4×(6-1)+4=4×5+4
……
50×52=50×52-50+50=50×(52-1)+50
=50×51+50
将上面各式左、右两边分别相加,可以得到
1×3+2×4+3×5+4×6+……+50×52
=1×2+1+2×3+2+3×4+3+4×5+4+……+50×51+50
=1×2+2×3+3×4+4×5+……+50×51+1+2+3+4+……+50
=44200+1275
=45475
例14 计算(1+0.23+0.34)× (0.23+0.34+0.56)-
(1+0.23+0.34+0.56)×(0.23+0.34)
分析与解 根据题中给出的数据,设1+0.23+0.34=a,0.23+0.34=b,那么 a-b=1+0.23+0.34-0.23-0.34=1。
于是原式变为
a×(b+0.56)-(a+0.56)×b
=ab+0.56a-ab-0.56b
=0.56a-0.56b
=0.56(a-b)
=0.56×1
=0.56
例15 算式2×3×5×7×11×13×17最后得到的乘积中,所有数位上的数字和是多少?
分析与解 要求算式乘积的各个数位上的数字和是多少,就要先求出乘积来。求积时应用乘法结合律可使计算简便。
2×3×5×7×11×13×17
=(2×5)×(7×11×13)×(3×17)
=10×1001×51
=10010×51
=510510
因此,乘积的所有数位上的数字和是
5+1+0+5+1+0=12
答:乘积的所有数位上的数字和是12。
分析与解 根据已知,要是算出两个数的乘积再求出积的各个数位的数字和,那就太复杂了。不妨先从简单的算起,寻找解题的规律。
例如,9×9=81,积的数字和是8+1=9;
99×99=9801,积的数字和是 9+8+1=18;
999×999 =998001,积的数字和是
9+9+8+1=27;
9999×9999=99980001,积的数字和是
9+9+9+8+1=36;
……
从计算的结果可以看出,一个因数中9的个数决定了积的各个数位的数字之和是几。
9×9的每个因数中有1个9,那么积的各个数位的数字和就是1个9;
99×99的每个因数中有 2个9,那么积的各个数位的数字和就是2个9,即等于18;
999×999的每个因数中有 3个 9,那么积的各个数位的数字和就是3个9,即等于27;
个9,即等于9×1993=17937。
分析与解 比较几个分数的大小时通常采用的方法是先将几个分数通分,再比较它们的大小;或者将几个分数先化成小数,再比较它们的大小。观察题中给出的五个数,不难发现,采用前面提到的这两种方法都不容易。但是在观察这几个分数时我们也不难发现,这几个分数的分子都比较小,并能看出3、2、15、10、12的最小公倍数是60,那么就应该把这几个分数都化成分子相同的分数,去比较它们的大小。我们知道,分子相同的分数,分母大的反而小,分母小的反而大。
还是比B小?
例19 1~1994这些自然数中所有数字的和是多少?
分析与解 要求1~1994这些自然数中所有数字的和,可以先求出0~1999这些数中所有数字的和,然后再减去1995~1999这五个数的数字和。
将0~1999这2000个数分组,每两个数为一组,可以分成1000组:
(0,1999),(1,1998),(2,1997),(3,1996),(4,1995),……,(996,1003),(997,1002),(998,1001),(999,1000)。
这里每组的两数的和都是1999,并且每组中两个数相加时都不进位,这样,1~1999这些自然数所有数字和是:
(1+9+9+9)×1000=28×1000= 28000
而 1995~1999这五个数的数字和是:
(1+9+9)×5+(5+6+7+8+9)=95+35=130
因此1~1994这些自然数中所有数字的和是:
28000-130=27870
答:1~1994这些自然数中所有数字的和是27870。
分析与解 要是先计算出正确的结果,再回答题中所问的这个繁分数化简后整数部分是多少,那可不是简单的计算。
这个繁分数的分子是1,那么这个繁分数化简后的结果,不就是这个繁分数分母部分各个分数之和的倒数吗?因此,只要看看分母部分是多少就可以了。
个分数相加。
然这个繁分数化简后的结果就是1了。
繁分数化简后的整数部分就是1了。
几何初步知识
小学生学习几何初步知识,不仅要掌握一些基本的平面图形和立体图形的性质、特征,还要会求这些平面图形的周长、面积及这些立体图形的表面积、体积,而且还要会综合地、巧妙地运用这些知识来进行计算。特别是计算一些组合图形的面积时,常常用到割补、剪拼、平移、翻转等办法,使得计算巧妙、简便。要学会这些方法,应用这些方法。通过解几何题的训练,更好地培养空间想象力,这对学好小学几何初步知识是极有利的,同时也为将来到中学进一步学习几何知识,打下良好而坚实的基础。
例21 下图中圆O的面积和长方形OABC的面积相等。已知圆O的周长是9.42厘米,那么长方形OABC的周长是多少厘米?
分析与解 题中告诉我们,圆O的面积和长方形OABC的面积相等。我们知道,圆的面积等于π·r·r,而图中圆O的半径恰好是长方形的宽,因此长方形OABC的长正好是π·r,即圆O的周长的一半。而长方形的周长等于2个长与2个宽的和,也就是圆O的周长与直径的和。
长方形OABC的周长是:
9.42+9.42÷3.14
=9.42+3
=12.42(厘米)
答:长方形OABC的周长是12.42厘米。
例22 桌面上有一条长80厘米的线段,另外有直径为1厘米、2厘米、3厘米、4厘米、5厘米、8厘米的圆形纸片若干张,现在用这些纸片将桌上线段盖住,并且使所用纸片圆周长总和最短,问这个周长总和是多少厘米?
分析与解 要想盖住桌上线段,并且使所用纸片圆周长总和最短,那么盖住线段的圆形纸片应该是互不重叠,一个挨一个地排开,这时若干个圆形纸片直径的总和正好是80厘米。这些圆形纸片周长的总和与直径为80厘米的圆的周长相等,因此盖住桌子上线段的若干个圆形纸片的周长总和是:
3.14×80=251.2(厘米)
答:这个周长总和是251.2厘米。
例23 图2为三个同心圆形的跑道,跑道宽1米。某人沿每条圆形跑道的中间(虚线所示)各跑了1圈,共3圈。他一共跑了多少米?
分析与解 根据题意,要求某人一共跑了多少米,就是求半径分别为1.5米、2.5米和3.5米的三个圆的周长之和。列式为
3.14×(1.5×2)+3.14×(2.5×2)+3.14×(3.5×2)
=3.14×3+3.14×5+3.14×7
=3.14×(3+5+7)
=3.14×15
=47.1(米)
还可以这样思考:
如果这个人拿着一个1米宽的拖把,边跑边拖地,他跑了1个圆圈,就把这一圈的跑道全拖干净。那么他跑了3个圆圈,就把这三条圆形跑道全拖干净了。他共拖了3个环形面积的地。这3个环形面积的总和是
3.14×(42-32)+3.14×(32-22)+3.14×(22-12)
=3.14×(42-32+32-22+22-12)
=3.14×(42-12)
=3.14-[(4+1)×(4-1)]
=3.14×15
=47.1(平方米)
当然,也可以直接列式:3.14×(42-12)=47.1(平方米)
因为跑道宽1米,这个人拖完47.1平方米,那么他就前进了47.1米。
答:一共跑了47.1米。
这里列举的只是某人跑了3个圆形跑道。如果将题改为跑100个这样的圆形跑道,那么用后面介绍的解法计算他跑步的总长度,就简捷多了。
解法如下:
3.14×(1012-12)
=3.14×(101+1)×(101-1)
=3.14×102×100
=32028(平方米)
因为跑道宽1米,所以共跑了32028米。
例24 在面积是40平方厘米的正方形中,有一个最大的圆(如图3)。这个圆的面积是多少平方厘米?
分析与解 要求圆的面积,就要先求出圆的半径。题中告诉我们,正方形的面积是40平方厘米,正方形的边长的一半,也就是图中圆的半径。对小学生来讲,从正方形的面积求正方形的边长,还不会直接计算。
可以这样思考:
把正方形平均分成4份(如图4)。每个小正方形的面积是40÷4=10平方厘米。小正方形的边长恰好是圆的半径,因此圆的半径的平方恰好是10平方厘米。这样就可以求出圆的面积是3.14×10=31.4平方厘米了。
答:图中圆面积是31.4平方厘米。
例25 图5由正方形ABCD和长方形EFDG部分重叠而成。正方形的边长是247.8厘米;长方形的长是292.404厘米、宽是210厘米,正方形和长方形哪个面积大?
分析与解 要比较正方形ABCD和长方形EFDG面积的大小,方法是分别算出它们的面积再进行比较。从题中给出的数据看,确实给计算带来麻烦。
只要在AF两点间连一条线段(如图6),就会发现,三角形 AFD的面积是正方形 ABCD面积的一半,同时也是长方形EFDG面积的一半,所以正方形ABCD和长方形EFDG的面积一样大。这样,也就不用计算这两个图形的面积了。
例26 图7由半圆和等腰直角三角形重叠而成。已知等腰直角三角形的直角边长为4厘米,求图中阴影面积。
分析与解 如果分别算出两个阴影部分的面积,再把它们加起来,以便求出图中阴影部分的总面积,那就太复杂了。
根据题中的条件,我们可以把图中弓形阴影剪下来拼(或旋转)成图8。
从图8不难看出,题中要求的阴影部分的面积就是三角形 ABC面积的一半。
图中的阴影面积是:
(4×4÷2)÷2=4(平方厘米)
答:图中阴影面积是4平方厘米。
例27 有5个正方形(如图9),边长分别是1米、2米、3米、4米、5米。问图中白色部分面积与阴影部分面积的比是几比几?
分析与解 观察已知图形,显然,先计算出白色面积比较简单。
白色部分面积是:(22-12)+(42-32)=10(平方米)
阴影部分面积是:52-10=15(平方米)
因此,白色部分面积与阴影部分面积之比是:10∶15,即2∶3。
还可以这样想:作正方形的对角线AD和BC,两条对角线相交于O,于是两条对角线把正方形平均分成四部分(如图10)。
要计算整个图形中白色部分面积与阴影部分面积的比,只需计算三角形AOB中白色部分面积与阴影部分面积的比就可以了。在三角形AOB中,可把白色的和阴影的两部分图形都看作是一些梯形,其中把最上端的小阴影三角形看作是上底为O的梯形。这些梯形的高都相等,所以这些梯形面积之比就是这些梯形上、下底的和之比。
从小到大,5个梯形面积比是:
1∶(1+2)∶(2+3)
∶(3+4)∶(4+5)=1∶3∶5∶7∶9
因此,图中白色部分面积与阴影部分面积的比是:(3+7)∶(1+5+9)=2∶3
答:图中白色部分面积与阴影部分面积比是2∶3。
例28 有一个直角梯形ABCD,已知AB=8厘米,CD=4厘米,BC=6厘米,三角形ABF的面积比三角形EFD的面积大17.4平方厘米,那么ED长多少厘米?
分析与解 连接DB(图12)。已知三角形ABF比三角形EFD的面积大17.4平方厘米,所以三角形ABD比三角形BED的面积也大17.4平方厘米。
三角形BDE的面积是:24-17.4=6.6(平方厘米)。而三角形 BDE的面积等于ED×BC×1/2
即ED×6×1/2=6.6
所以ED长是2.2厘米。
答:ED的长是2.2厘米。
例29 图13由4个正六边形拼成,每个正六边形的面积都是6,那么三角形ABC的面积是多少?
分析与解 首先连接每个正六边形的对角线,将每个六边形平均分成六个小的正三角形(如图14),那么每一个小三角形的面积都是1。
由图14不难看出:三角形ABC是由三角形DEF、三角形AEB、三角形BDC和三角形CFA组成的,其中三角形DEF的面积是4,而其它的三个三角形面积都相等。
先看三角形ABE。它正好是平行四边形AGBE的一半,而平行四边形AGBE的面积是6,因此,三角形ABE的面积是3。当然,三角形BDC和三角形CFA的面积也是3。
由此得出三角形ABC的面积是
4+3×3=13
答:三角形ABC的面积是13。
例30 已知图15中正方形ABCD的面积是256平方厘米,那么正方形EFGH的面积是多少平方厘米?
分析与解 将图15中正方形A0′B′C′D′旋转成图16。由图中不难看出:正方形 A′ B′C′D′的面积是正方形ABCD面积的1/2;正方形EFGH的面积是正方形A′B′C′D′的面积的1/2。因此,正方形
已知正方形ABCD的面积是256平方厘米,所以正方形EFGH的面积是
答:正方形EFGH的面积是64平方厘米。
例31 图17是一个正方形地板砖示意图,在大正方形ABCD中,AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?
分析与解 连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在DPC处(如图18和图19)。
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。由此得出,正方形OCPD的边长是4+6=10厘米,当然正方形OCPD的面积就是102,即100平方厘米。而正方形OCPD的面积恰好是正方形ABCD的面积的一半,因此正方形ABCD的面积是200平方厘米。
答:正方形ABCD的面积是200平方厘米。
例32 一个任意凸六边形ABCDEF,P、Q、M、N分别为AB、BC、DE和EF边上的中点。已知阴影部分的面积是100平方厘米,那么六边形ABCDEF的面积是多少平方厘米?
分析与解 连接BF、 BE、 BD,在三角形ABF中,P是AB的中点,那么三角形BPF和三角形APF是等底等高的三角形。因此三角形BPF和三角形APF的面积相等。
同理,由于N为EF中点,所以三角形FNB和三角形 ENB的面积相等;由于M为DE中点,所以三角形DMB和三角形EMB的面积相等;由于Q为BC中点,所以三角形BQD和三角形CQD的面积相等。
由此得出:三角形BPF+三角形BQD+三角形DMB+三角形FNB=三角形APF+三角形CQD+三角形EMB+三角形ENB。
而三角形BPF+三角形BQD+三角形DMB+三角形FNB=阴影面积=100平方厘米,所以三角形APF+三角形CQD+三角形EMB+三角形ENB=空白部分面积=100平方厘米。
因此,六边形 ABCDEF的面积为100×2=200平方厘米。
答:六边形ABCDEF的面积是200平方厘米。
例33 图21是一个圆形钟面,圆周被平均分成了12等份。已知圆形的半径是6厘米,那么图中阴影的面积是多少平方厘米?
分析与解 题中告诉我们:圆周被平均分成了12等份,因此连接OE,
由图中不难看出:三角形AOB与三角形EOB是等底同高的三角形,这两
的面积相等。
于是图中阴影的面积是:
答:阴影的面积是18.84平方厘米。例34图 23中四边形ABCD是一个正方形。E、F分别为CD和BC边上的中点。已知正方形ABCD的边长是30厘米,那么图中阴影部分的面积是多少平方厘米?
分析与解 已知四边形ABCD为正方形,E、F分别为CD边与BC边上的中点,因此,三角形BCE和三角形DCF面积相等。这两个三角形的面积各自减去四边形GFCE的面积,各自剩下的三角形GBF和三角形GDE面积还是相等的。
连接GC(如图24),三角形GBF面积和三角形GCF的面积是相等的,因为这两个三角形等底同高。同理,三角形GCE面积和三角形GDE的面积也是相等的。而三角形GBF的面积和三角形GDE的面积相等,因此,三角形GBF、三角形GCF、三角形GCE及三角形GDE是具有相等面积的四个三角形。
因为三角形BCE的面积等于正方形ABCD面积的1/4,所以图中空白部分的面积,即三角形GBF、三角形GCF、三角形GCE、三角形GDE的面积之和为正方形ABCD面积的
从而得出图中阴影部分的面积为正方形ABCD面积的
那么阴影部分的面积是:
答:图中阴影部分的面积是600平方厘米。
例35 为了美化校园,东升小学用鲜花围成了两个圆形花坛。小圆形花坛的面积是3.14平方米,大圆形花坛的半径是小圆形花坛半径的2倍。大圆形花坛的面积比小圆形花坛的面积大多少平方米?
分析与解 我们知道圆的面积与半径的平方成正比。题中告诉我们,大圆的半径是小圆半径的2倍,那么大圆面积是小圆面积的22倍。
大圆形花坛的面积比小圆形花坛的面积大
3.14×(22-1)
=3.14×3
=9.42(平方米)
答:大圆形花坛的面积比小圆形花坛的面积大9.42平方米。
例36 有两个长方形,甲长方形的长是98769厘米,宽是98765厘米;乙长方形的长是98768厘米,宽是98766厘米。这两个长方形的面积哪个大?
分析与解 利用长方形面积公式,直接计算出面积的大小,再进行比较,这是可行的,但是计算太复杂了。
可以利用乘法分配律,将算式变形,再去比较两个长方形的面积大小,这就简便多了。
甲长方形的面积是:
98769×98765
=98768×98765+98765
乙长方形的面积是
98768×98766
=98768×98765+98768
比较98768×98765+98765与98768×98765+98768的大小,一眼便能看出:甲长方形的面积小,乙长方形的面积大。
还有如下一种思考解答方法。
请先看看下面的事实。
周长相等的两个长方形,长与宽的差越大,则面积就越小;反之,长与宽之差越小,则面积就越大。当然,当长方形长与宽之差为0时,也就是为正方形时,面积则最大。
假设有两个长方形的周长是20厘米,那么周长的一半,也就是长与宽的和,是10厘米,列举出一部分长、宽的大小与面积的关系,就会得出上面所讲的事实是存在的,并且是正确的。
我们再回到原题。甲、乙两个长方形的长与宽的和是相等的(当然它们的周长也相等),即
98769+98765=98768+98766
而甲长方形长与宽的差是:
98769-98765=4(厘米)
乙长方形长与宽的差是:
98768-98766=2(厘米)
因为4厘米>2厘米,所以甲长方形的面积小,乙长方形的面积大。
答:乙长方形的面积大。
例37 一个红色的正方形ABCD,它的边长是1993厘米;另一个红色的正方形A′B′C′D′,它的边长是 1994厘米。一个绿色正方形EFGH,它的边长是1992厘米,另一个绿色正方形E′F′G′H′,它的边长是1995厘米。问两个红色的正方形的面积大,还是两个绿色的正方形面积大?
分析与解 要比较两个红色的正方形面积大,还是两个绿色的正方形面积大,可以先分别算出它们的面积,然后再进行比较。不过这样计算起来就太复杂了。
可以这样比较它们的大小:
先将红色正方形ABCD与绿色正方形EFGH重叠在一起(如图26)。
从图26不难看出,红色正方形ABCD的面积比绿色正方形EFGH的面积大的平方厘米数是:
1×1992+1×1+1×1992=2×1992+1
再将红色正方形A′B′C′D′与绿色正方形E′F′G′H′重叠在一起(如图27)。
从图27不难看出,红色正方形A′B′C′D′的面积比绿色正方形E′F′G′H′的面积小的平方厘米数是:
1×1994+1×1+1×1994
=2×1994+1
而2×1994+1>2×1992+1,也就是说绿色正方形E′F′G′H′比红色正方形A′B′C′D′大的面积数超过红色正方形ABCD比绿色正方形EFGH大的面积数。因此两个绿色正方形的面积大。
答:两个绿色正方形的面积大。
例38 在长方形ABCD中,AE的长度与ED的长度的比是8∶5;BF的长度与FC的长度的比是11∶7。那么涂红色的两块图形的面积与涂蓝色的两块图形的面积相比较,哪个大?
分析与解 要比较涂红色的两块图形的面积大,还是涂蓝色的两块图形的面积大,只要比较三角形AEC和三角形BDF的大小就可以了。因为这两个三角形各自减去重叠的那块四边形,剩下的就是两个涂红色的图形和两个涂蓝色的图形了。
因为ABCD是长方形,而三角形AEC和三角形BDF的高都是长方形ABCD的宽,所以比较三角形AEC和三角形BDF的大小时,只要比较AE和BF的大小就可以了。
根据已知,AE的长度与ED的长度的比是8∶5,那么AE的长度就占
即AE>BF,从而得出三角形AEC的面积大于三角形BDF的面积。
因此,涂红色的两块图形的面积大于涂蓝色的两块图形的面积。
答:涂红色的两块图形的面积大于涂蓝色的两块图形的面积。
例39 一块长方形小麦田,被互相垂直的两条直线分成A、B、C、D四部分。A的地积是45公亩,B的地积是20公亩,C的地积是36公亩。那么,D有多少公亩?
分析与解 观察图29不难发现,B与C的长是相等的,因此,B与C地积的比就是它们宽的比。A与D的长也是相等的,因此,A与D地积的比也是它们宽的比。而A与B,C与D的宽分别相等,于是
A∶D=B∶C
即 45∶D=20∶36
D=81
答:D有81公亩。
例40 有50个表面涂有红漆的正方体,它们的棱长分别是1厘米、3厘米、5厘米、7厘米、9厘米、……、99厘米,将这些正方体锯成棱长为1厘米的小正方体,得到的小正方体中,至少有一个面是红色的小正方体共有多少个?
分析与解 棱长为1厘米涂有红漆的小正方体,不用锯,就是棱长1厘米的小正方体,它当然是至少有一个面是红色的小正方体了。
将棱长为3厘米的涂有红漆的小正方体,锯成棱长为1厘米的小正方体,共得到33个,其中没有涂红漆的共(3-2)3个。
将棱长为5厘米的涂有红漆的小正方体锯成棱长为1厘米的小正方体,共得53个,其中没有涂红漆的共(5-2)3个。
将棱长为7厘米的涂有红漆的小正方体锯成棱长为1厘米的小正方体,共得73个,其中没有涂红漆的共(7-2)3个。
由以上分析、计算发现,将校长为1厘米、3厘米、5厘米、7厘米的四个正方体锯成棱长为1厘米的小正方体后,得到至少有一个面为红色的小正方体共有
13+33-(3-2)3+53-(5-2)3+73-(7-2)3
=13+33-13+53-33+73-53
=13+33+53+73-13-33-53=73=343(个)
按照这样的规律可得,将棱长为1厘米、3厘米、5厘米、7厘米、9厘米、……、99厘米这50个正方体锯成棱长为1厘米的小正方体后,得到至少有一个面为红色的小正方体共有:
13+33+53+73+93+……+973+993-13-33-53-73-93-……-973=993=970299(个)
答:至少有一个面是红色的小正方体共有970299个。
例41 有棱长为 1、2、3、……、99、100、101、102厘米的正方体102个,把它们的表面都涂上红漆,晾干后把这102个正方体都分别截成1立方厘米的小正方体,在这些小正方体中,只有2个面有红漆的共有多少个?
分析与解 根据题意,首先应该想到只有2个面有红漆的小正方体,都在原来大正方体的棱上。原来棱长是1厘米、2厘米的正方体,将它截成1立方厘米的小正方体后,得不到只有2个面有红漆的小正方体。棱长是3厘米的正方体,将它截成1立方厘米的小正方体后,大正方体的每条棱上都有1个小正方体只有2个面有红漆。每个正方体有12条棱,因此可得到 12个只有 2个面有红漆的小正方体,即共有(3-2)×12个。
棱长为4厘米的正方体,将它截成1立方厘米的小正方体后,得到只有 2个面有红漆的小正方体共(4-2)×12个。
依此类推,可得出,将这102个正方体截成1立方厘米小正方体后,共得到只有2个面有红漆的小正方体的个数是:
[(3-2)+(4-2)+(5-2)+……+(102-2)]×12
=[1+2+3+……+100]×12
=60600
答:只有2个面有红漆的小正方体共有60600个。
例42 有一个长方体木块,长125厘米,宽40厘米,高25厘米。把它锯成若干个体积相等的小正方体,然后再把这些小正方体拼成一个大正方体。这个大正体的表面积是多少平方厘米?
分析与解 一般说来,要求正方体的表面积,一定要知道正方体的棱长。题中已知长方体的长、宽、高,同正方体的棱长又没有直接联系,这样就给解答带来了困难。我们应该从整体出发去思考这个问题。
按题意,这个长方体木块锯成若干个体积相等的小正方体后,又拼成一个大正方体。这个大正方体的体积和原来长方体的体积是相等的。已知长方体的长、宽、高,就可以求出长方体的体积,这就是拼成的大正方体的体积。进而可以求出正方体的棱长,从而可以求出正方体的表面积了。
长方体的体积是
125×40×25=125000(立方厘米)
将 125000分解质因数:
125000=2×2×2×5×5×5×5×5×5
=(2×5×5)×(2×5×5)×(2×5×5)
可见大正方体的棱长是
2×5×5=50(厘米)
大正方体的表面积是
50×50×6=15000(平方厘米)
答:这个大正方体的表面积是15000平方厘米。
例43 一个正方体形状的木块,棱长2分米。沿水平方向将它锯成3片,每片又锯成4条,每条又锯成5小块,共得到大大小小的长方体60块(如图30)。这60块长方体表面积的和是多少平方分米?
分析与解 解答这道题的最直接的想法是将这大大小小的60个长方体形状的小木块的表面积分别计算出来,然后再求出总和,这样做是可以的,但计算极为复杂。因此解答这题时,应从整体出发,这样,问题就简单多了。
这个正方体形木块在未锯成60个长方体形状的小木块前,共有6个面,每个面的面积是2×2=4平方分米,6个面共24平方分米。不管后来锯成多少块小长方体,这6个面的24平方分米的面积总是后来的小长方体的表面积的一部分。
现在我们来考虑将木块每锯一刀的情况。显然,每锯一刀就会增加2个4平方分米的表面积,根据题意,现在一共锯了2+3+4=9刀,共增加了18个4平方分米的表面积。
因此,这60块大大小小的长方体的表面积总和是
24+4×18=96(平方分米)
或列式为
2×2×[6+(2+3+4)×2]
=4×[6+18]
=4×24
=96(平方分米)
答:60块长方体表面积的和是96平方分米。
例44 一个圆柱体,底面半径是5厘米,这个圆柱体的侧面积是100平方厘米。它的体积是多少立方厘米?
分析与解 一般的解法是先求出圆柱体的高和底面积,再求圆柱体的体积。
圆柱体的高:
圆柱体的底面积:
3.14×52=78.5(平方厘米)
圆柱体的体积:
我们已知学过,用切拼的方法,可以把一个圆柱体切拼成一个与它等体积的近似的长方体(如图31)
观察图31不难发现,圆柱体的体
积等于侧面积的一半与底面半径的乘积,即
用这个式子计算题中圆柱体的体积,就比用一般的方法计算要简便多了。
答:圆柱体的体积是250立方厘米。
应用题部分
应用题就是应用数学概念及运算意义去解答的实际问题。因此学好数学概念和各种运算意义是会解应用题的基础。
怎样运用数学概念及运算意义去解应用题呢?首先是要用数学概念去分析题中的数量关系。这种分析应该说是全面的、深刻的。要分析已知数量与已知数量,已知数量与未知数量间的关系。然后根据运算意义,用式子表示出题中要求的数量,使问题得到解决。
小学生在分析应用题中数量关系时,常常缺少更深的思考,只满足于得出一般的解答方法,这是不够的。重要的是通过全面的、深刻的分析,综合运用数学概念、运算意义,会寻找巧妙的解法,这对发展小学生观察比较、分析综合、判断推理、想象类比的能力是极为有利的。
牢固而清晰地掌握数学概念、运算意义才能使你去深刻地思考问题。也要学会一些帮你思考的方法。比如把题中的条件排列出来,画一画示意图、线段图等,总之,把题中的条件、问题形象化是一种常见的、有效的办法。它能帮你想得更深刻。
解答应用题最忌讳死背题型、死记解题模式,这样往往束缚了你的手脚。时间久了,你的思维就僵化了,这对今后的学习极为不利。
例45 红花衬衫厂要制做一批衬衫,原计划每天生产400件,60天完成。实际每天生产的件数是原计划每天生产件数的1.5倍。完成这批衬衫的制做任务,实际用了多少天?
分析与解 要求完成这批衬衫的制做任务,实际用了多少天,必须知道这批衬衫的总数和实际每天生产的件数。已知原计划每天生产400件,60天完成,就可以求出这批衬衫的总数量;又知道实际每天生产的件数是原计划生产件数的1.5倍,就可以求出实际每天生产的件数。
完成这批衬衫的制做任务,实际用的天数是:
400×60÷(400×1.5)
=24000÷600
=40(天)
也可以这样想:要生产的衬衫的总数量是一定的,所以,完成这批衬衫制做任务所需要的天数与每天生产衬衫的件数成反比例关系。由此可得,实际完成这批衬衫制做任务的天数的1.5倍,正好是60天,于是得出制做这批衬衫实际需要的天数是:
60÷1.5=40(天)
答:完成这批衬衫制做任务,实际用了40天。
例46 东风机器厂原计划每天生产240个零件,18天完成。实际比原计划提前3天完成,实际每天比原计划每天多生产多少个零件?
分析与解 要求实际每天比原计划每天多生产多少个零件,得先求出实际每天生产多少个零件,再减去计划每天生产的零件数:
240×18÷(18-3)-240
=4320÷15-240
=288-240
=48(个)
也可以这样想:实际与计划所完成的零件总数是相同的。根据反比例意义可知,每天生产零件的个数与完成生产这批零件所用的天数成反比例关系。由此可知,原计划完成任务的天数与实际完成任务的天数比18∶(18-3)即 6∶5,就是实际每天生产零件的个数与原计划每天生产零件个数的比。当然,实际每天生产零件的个数是原计划每天生产零件的个数的6/5。于是求出实际每天比原计划每天多生产零件的个数是:
=48(个)
还可以这样想:生产零件的总数是 240×18=4320(个);把这个数分解质因数,然后再把分解的质因数适当地分组,分别表示出原计划每天生产的个数与完成天数的乘积和实际每天生产的个数与实际完成天数的乘积。
4320=25×33×5
=(24×3×5)×(2×32)……原计划每天生产的个数与完成
天数的乘积
=(25×32)×(3×5)……实际每天生产的个数与完成天数的
乘积
进而求出实际每天比原计划每天多生产的个数是:
25×32-24×3×5
=288-240
=48(个)
答:实际每天比原计划每天多生产48个。
例47 在春光小学“创造杯”展览会上,展品中有36件不是六年级的,有37件不是五年级的,又知道五、六两个年级的展品共有45件。那么,五、六年级的展品各有多少件?
分析与解 根据已知,有36件不是六年级的,就是说,1~4年级的展品加上五年级的展品共有36件。有37件不是五年级的,就是说,1~4年级的展品加上六年级的展品共有37件。
比较以上两个条件,可以得出,六年级比五年级的展品多37-36=1件。
又知道五、六两个年级的展品共有45件,于是求出五年级的展品有
(45-1)÷2=44÷2=22(件)
六年级的展品有
(45+1)÷2=46÷2=23(件)
答:五年级的展品有22件,六年级的展品有23件。
例48 机械厂零件加工组里有1位师傅和6位徒弟,共7人。徒弟每人每天能加工零件50个,师傅每天加工零件的个数比全组7个人每天平均加工的个数多24个。师傅每天加工零件多少个?
分析与解 师傅每天加工零件的个数比全组7个人平均每天加工的个数多24个。把这24个平均分给6位徒弟,再加上徒弟每天加工的50个,正好是7个人平均每天加工的个数。这个数再加上24就是师傅每天加工零件的个数。
24÷6+50+24
=4+50+24
=54+24
=78(个)
答:师傅每天加工零件78个。
例49 儿童服装厂生产红上衣和黄上衣。每件红上衣需要2个钮扣,每件黄上衣需要4个钮扣。做成的两种颜色的上衣,每30件装成一箱,每箱衣服共需要钮扣72个。每箱中有红上衣和黄上衣各多少件?
分析与解 已知每件黄上衣要用4个钮扣,每件红上衣要用2个钮扣。如果将黄上衣一分为二,黄上衣就成为“半件黄上衣”了。这时红上衣和“半件黄上衣”都需要2个钮扣。已知每箱中两种颜色的上衣共需要钮扣72个,于是可以求出红上衣和“半件黄上衣”共有72÷2=36(件)。实际每箱中两种颜色的上衣共30件,36件比30件多了6件,说明有6件黄上衣被一分为二了,所以每箱中有6件黄上衣。进而求出每箱中红上衣的件数是 30-6=24(件)
列式为:
72÷2-30=36-30=6(件)
30-6=24(件)
还可以这样思考:
把每箱中的30件上衣,每件都取下2个钮扣,这样红上衣就没有钮扣了,黄上衣每件上还剩下2个钮扣,共取下2×30=60个钮扣。这时箱内的上衣上还剩下72-60=12个钮扣。因为只有每件黄上衣上还剩下2个钮扣,所以12÷2=6(件)就是每箱中黄上衣的件数。那么,每箱中红上衣的件数就是 30-6=24(件)了。
列式为:
(72-2×30)÷(4-2)
=(72-60)÷2
=12÷2
=6(件)
30-6=24(件)
答:每箱中有红上衣24件,有黄上衣6件。
例50 主人的篮子里放着苹果和桃。苹果的个数是桃的3倍。一群顽皮的小猴,趁主人不注意的时候,每只小猴子都拿了8个苹果和3个桃。主人发现时,桃子已被小猴拿光了,还剩下10个苹果。这群顽皮的小猴一共有多少只?
分析与解 篮子里的苹果的个数是桃的3倍,每只小猴子拿了3个桃子,而且拿光了,那么要是每只小猴子拿9个苹果,也可以把苹果拿光(因为苹果个数正好是桃个数的3倍)。可是,每只小猴子只拿了8个苹果,结果还剩下10个苹果,这正好说明这群小猴子共有10只。
答:这群顽皮的小猴一共有10只。
例51 光明小学原计划192天烧煤91800千克。如果每天比原计划节约
分析与解 要求节约出来的煤还可以再烧几天,就必须知道一共节约出来多少煤和节约后每天的烧煤量。
一共节约出来多少千克的煤?
节约出来的煤还可以再烧多少天?
5400÷450=12(天)
还可以这样想:
17个单位,那么实际每天节约用煤为1个单位,实际每天用煤为16个单位。原计划烧煤192天,一共可以节约出192个单位的煤,这些煤还可以烧:
192÷16=12(天)
答:节约出来的煤还可以再烧12天。
例52 有1993个人和1993斤面粉。第1个人拿走了全部面粉的1/2,第2个人拿走了余下面粉的1/3,第3个人拿走了再余下的1/4,……第1992
走了。那么第1993个人拿走了多少斤面粉?
分析与解 解答这道题不宜采用分步计算的方法。1993斤面粉被第1个人拿走1/2,剩下的当然是全部的1/2,这一算就出现了小数,再算第2个人拿走后剩下多少斤面粉就更复杂了。因此解答时应从整体去思考,列综合算式解答,就简便多了。依题意列式为
答:第1993个人拿走了1斤面粉。
分析与解 根据题意,从第10天、第9天,……倒推回去,列式求出这批面粉原来共有
=40(袋)
也可以这样想:
这些面粉共吃了10天,把这堆面粉平均分成10堆。第1天吃了这批面
每天吃的都是平均分成10堆中的1堆,第10天吃的那一堆正好是4袋,因此,这批面粉共有
4×10=40(袋)
答:这批面粉原来共有40袋。
例54 有两个容器,第一个容器中有1升水,第二个容器是空的。将第一个容器中的水的1/2倒入第二个容器中,然后将第二个容器里的水的1/3倒回第一个容器中,然后再将第一个容器里的水的1/4倒入第二个容器中,……如此进行下去,倒了1993次后,第一个容器里有多少水?
分析与解 根据题意,把倒的次数、两杯中水的数量列成下表。
从上表不难看出,凡是倒了1、3、5、……奇数后,第一个容器里的水都是1/2升。当然,倒了1993次后,第一个容器里的水也是1/2升。
也可以列式计算:
例55 幼儿园小朋友过“六一”儿童节,阿姨给小朋友分苹果,开始每人分3个,结果有15个人只分到2个;后来又买来40个苹果,又分给小朋友,结果正好每个分到4个。幼儿园一共有多少个小朋友?
分析与解 题中告诉我们,开始每人分3个,结果有15个小朋友只分到2个,就是说,每人分3个缺少15个苹果。后来又买来40个苹果,又分给小朋友,结果正好每人分到4个。把这40个苹果先拿出15个,分给开始分时每人只分到2个苹果的那些小朋友,这时还剩下25个苹果,每人再分1个,正好是每人分到4个苹果。因此得出,幼儿园共有25个小朋友。
(40-15)÷(4-3)
=25÷1
= 25(人)
答:幼儿园一共有25个小朋友。
例56 一个箱子里装满了实心球,连箱子共重12千克。从箱中取出实心球的1/4后,剩下的实心球连箱共重9.5千克。问箱子重多少千克?
分析与解 一个箱子里装满了实心球,连箱子共重12千克;从箱中取实心球的1/4后,剩下实心球的3/4连箱子共重9.5千克。由此可以得出,实心球的1/4重(12-9.5)千克,那么实心球的总重是:
=10(千克)
箱子重量是:
12-10=2(千克)
答:箱子重2千克。
分析与解 把绳子的全长看作“1”,把绳子折成三股来量,就是用绳长的1/3来量;把绳子折成四股来量,就是用绳长的1/4来量。井外所余绳子长度之差就是绳长1/3与绳长1/4之差。于是得到绳子的全长是:
也可以这样想:
正好是绳子的长度。
正好是绳子的长度。
好是井的深度。
于是求出井的深度是:
例58 同学们搞野营活动。一个同学到负责后勤工作的老师那里去领碗。老师问他领多少,他说领55个。又问“多少人吃饭?”他说:“一个人1个饭碗,两个人1个菜碗,三个人1个汤碗。”请算一算这个同学给参加野营活动的多少人领碗?
分析与解 先算出平均1人要用多少个碗,再算出多少人需要55个碗。列式是
还可以这样解答:
吃饭时每人1个饭碗,要用多少个饭碗,就表示有多少人参加野营活动。题中又说,两个人1个菜碗,三个人1个汤碗。我们知道,2和3的最小公倍数是6,就是说,当有6个人吃饭时,要用6个饭碗,3个菜碗,2个汤碗。于是得出有6个人吃饭时,共需要6+3+2=11个碗。
于是,我们把参加野营活动的人,分成每6个人一组,每组人吃饭时要用11个碗。
由55÷11=5可以知道,领55个碗说明吃饭的人正好分成了5组,于是求出这个同学要给6×5=30人领碗。
答:这个同学给参加野营活动的30人领碗。
大2岁。那么父亲几岁?母亲几岁?儿子几岁?
分析与解 题中告诉我们,儿子的年龄是母亲年龄的3/10,是父亲年龄的2/7,就是说,母亲年龄
的3/10等于父亲年龄的2/7。由此可知,母亲年龄的21/70岁,这时父亲比母亲大1岁。
题中告诉我们,父亲年龄比母亲大2岁,因此可知,母亲为 40岁,父
答:父亲42岁,母亲40岁,儿子12岁。
例60教室里有一些男生和一些女生。老师问他们人数。一个男生告诉老
分析与解 题中告诉我们,除去1个男生,男生人数是女生人数的
题中还告诉我们,除去1个女生,女生人数是男生人数的3/5。
示女生人数,除去1个女生,正好是9个女生。分母部分的15恰好表示男生人数,除去1个男生,正好是14个男生。
由此得出,教室里有男生15人,女生10人。
答:教室里有男生15人,女生10人。
例61 某书店原有书若干本,第一天售出全部的1/2,第二天又运进900本,第三天售出的书比现有的书的1/3还多40本,结果还剩下800本。书店里原有书多少本?
分析与解 根据题中给出的条件,可以倒推回去,求出书店里原有书多少本。
假设第三天售出的书比现有的书的1/3不多40本(即少售了40本),
,于是可以求出第三天售书前书店里有书多少本。
假设第二天不运进900本,这时书店里的书恰好是第一天卖出原来的书
求出书店里原有书的本数。
=720(本)
答:书店里原有书720本。
例62 有7袋米,它们的重量分别是 12千克、 15千克、17千克、20千克、22千克、24千克、26千克。甲先取走一袋,剩下的由乙、丙、丁取走。已知乙和丙取走的重量恰好一样多,而且都是丁取走重量的2倍。那么甲先取走的那一袋的重量是多少千克?
分析与解 题中告诉我们,甲先取走一袋后,剩下的由乙、丙、丁取走。已知乙和丙取走的重量恰好一样多,而且都是丁取走的重量的2倍,因此乙、丙、丁三人取走的重量是了取走的重量的5倍。
而7袋米的总重量是
12+15+17+20+22+24+26=136(千克)
从136中减去5的倍数,剩下的就是甲取走的重量的千克数。或者说,从136千克中减去甲取走那袋米的重量,剩下的重量一定是5的倍数。要使136减去一个数后得数能被5除尽,这个数的个位数字一定是1或6。而题中列出的7袋米的重量的千克数只有26的个位数字为6,因此甲先取走的那一袋米的重量是26千克。
答:甲先取走的那一袋米的重量是26千克。
例63 有若干堆围棋子,每堆围棋子的数目一样多,并且每堆中的白棋子占28%。明明从第一堆中拿走一半棋子,而且都是黑棋子。现在在所有的棋子中,白棋子占32%。那么原来共有几堆围棋子?
分析与解 根据题意,白棋子的个数在明明取走棋子的前后是没有变化的。由于取走了黑棋子,棋子总数有了变化,所以白棋子占棋子总数的百分数就发生变化,原来白棋子占总数的28%,而后来占总数的32%。由此可知,
答:原来共有4堆围棋子。
例64 植树节那天,学校把一批树苗分给三~六年级部分学生去植。如果由三年级的部分学生单独去植,平均每人植6株;如果由四年级的部分学生单独去植,平均每人植12棵;如果由五年级的部分学生单独去植,平均每人植20棵;如果由六年级的部分学生单独去植,平均每人植30棵。现在由三、四、五、六4个年级的部分学生都去植,平均每人植几棵?
分析与解 不管由几年级去植树,树苗的总数是一定的。设要植的树苗
生都去植树,平均每人植的棵数是
还可以这样想:根据题中给出的三~六年级单独去植树时平均每人植的棵数,可以推得,要植树的总棵数一定是6、12、20、30这四个数的公倍数。这四个数的最小公倍数是60。假设要植60棵树,那么不难算出三~六年级的人数分别是10人、5人、3人、2人,于是求出三~六年级的部分学生都去植树时,平均每人植的棵数是:
答:三、四、五、六4个年级的学生都去植树时,平均每人植3棵树。
例65 一件工程,如果甲先独做12天,然后乙再单独做9天,正好完成;如果乙先独做21天,然后甲再独做8天,也正好完成。如果这件工程由甲单独做,几天可以完成?
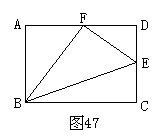
分析与解 题中所给的条件可用图49表示。
从图49不难看出,完成相同的工作量(图中双竖线中间部分),甲要用12-8=4(天),乙要用21-9=12(天),从而求出,在完成相同的工作量时,甲、乙所用时间的比为4∶2即1∶3。因此,甲单独完成这件工程要用
答:这件工程由甲单独做,15天可以完成。
例66 某水池可以用甲、乙两个水管注水。单开甲管,要10小时把空池注满;单开乙管,要20小时把空池注满。现在要求用8小时把空池注满,并且甲、乙两管合开的时间要尽可能地少,那么甲、乙两管合开最少要几小时?
分析与解 因为甲管注水较快,所以甲管应一直开着,8小时可给空池注水
开乙管的时间是:
即甲、乙两管合开的最少的时间是4小时。
也可以这样想:因为甲管注水较快,所以甲管应该一直开着。由于单开甲管10小时才能把空池注满,所以单开甲管8小时,还差甲管再开2小时的水量才能把空池注满。已知注满水池单开甲管要10小时,单开乙管要20小时,因此,单开甲管2小时的水量,就是单开乙管4小时的水量,即乙管要开4小时、也就是甲、乙两管合开的最少时间是4小时。
答:甲、乙两管合开最少要4小时。
例67 一件工程,甲独做20天可以完成;乙独做30天可以完成。现在由甲、乙合做,因为乙途中休息了几天,结果经过14天才完成任务。那么乙途中休息了几天?
分析与解 题中告诉我们,由于乙在甲、乙合做全工程中休息了几天,结果经过14天才完成任务。假设乙途中没有休息,那么甲、乙合做14天就会超过全部工程量,而超过的部分恰好是乙由于休息而没有干的,于是求出乙途中休息的天数是:
=5(天)
答:乙途中休息了5天。
例68 一件工程,甲乙丙三队合做,要8天完成。已知甲队每天的工作效率等于乙、丙两队每天的工作效率之和,丙队每天的工作效率相当于甲、乙两队每天工作效率和的1/5,那么这件工程如果由乙队单独去做,要几天才能完成?
分析与解 题中告诉我们,甲队每天的工作效率等于乙、丙两队每天的工作效率之和,丙队每天的工作效率相当于甲、乙两队每天工作效率之和的
题中还告诉我们,甲乙丙三队合做这件工程,8天可以完成,甲队每天工作效率又等于乙丙两队每天工作效率之和,所以这件工程如果由甲队独做,
由此得出,乙单独完成这件工程要用的天数是:
16÷2×3=24(天)
答:这件工程若由乙队单独去做,要24天才能完成。
例69 一项工程,如果由第一、二、三小队合干,需要12天才能完成;如果由第一、三、五小队合干,需要7天才能完成;如果由第二、四、五小队合干,需要8天才能完成;如果由第一、三、四小队合干,需要42天才能完成。现在由这五个小队一起干这项工程,几天才能完成?
分析与解 要求这五个小队一起干时完成这项工程需用的天数,先要求出这五个小队工作效率之和。设这五个小队的工作效率分别为A、B、C、D、E。根据已知可得
将上面四式相加,得
即3(A+B+C+D+E)=1/2
所以 A+B+C+D+E=1/6
因此,第一、二、三、四、五小队合干这项工程,要用
答:五个小队合干这项工程,6天可以完成。
例70 一个水池底部要用一个常开的排水管,上部要有若干个同样粗细的进水管。当打开4个进水管时,需要5小时才能注满一池水;当打开2个进水管时,需要15小时才能注满一池水。现要需要在2小时内注满一池水,那么至少需要打开几个进水管?
分析与解 假设每个进水管每小时进水量为1,那么打开 4个进水管, 5小时的进水量为 4×5=20。
打开2个进水管,15小时的进水量为2×15=30。
比较上面得出的结果,不难求出,排水管每小时的排量为
(30-20)÷(15-5)=1
进而求出满池的水量为
20-1×5=15或30-1×15=15
那么,要在2小时内注满水池,至少要打开的进水管为:
(15+1×2)÷2=8.5≈9(个)
答:至少要打开9个进水管。
例71 甲、乙二人同时从A地出发沿同一条路去B地,甲的速度始终不变,而乙在行走AB间的前1/5路程时的速度是甲速度的2倍,在行走后AB
时间少,因此甲先到达B地。
答:甲先到达B地。
例72 从A城到B城,甲要行2小时,乙要行1小时40分钟。如果甲先行10分钟,那么乙出发后多少分钟,在何处追上甲?
分析与解 根据已知,从A城到B城,甲比乙要多用
60×2-(60+40)=20(分钟)
也就是说,如果甲比乙早出发20分钟,二人就可以同时到达B城。现在甲比乙早出发10分钟,即甲先行10分钟后乙再出发,那么二人就会同时到达A、B两城间的中点处。
到达两城间的中点处,乙要用50分钟,这就是说,乙出发50分钟,在A、B两城间的中点处追上甲。
答:乙出发后50分钟,在两城间中点处追上甲。
例73 一辆客车和一辆货车同时从甲、乙两地相向开出,客车行了甲、乙两地间全程的3/5时,恰好和货车相遇。相遇后货车仍以原来每小时行40千米的速度向甲地驶去,又用了18小时到达甲地。求客车的速度。
分析与解 题中要求客车的速度,那么就要先求出客车行驶的路程和行驶这段路程所用的时间。题中已知客车和货车同时从甲、乙两地相向而行,客车行了甲、乙两地间全程的3/5与货车相遇,这时货车行了甲、乙两地全程的2/5。货车仍以原速(每小时40千米)又行了18小时到达甲地,即用了18小时走了全程的3/5,这样可以求出甲、乙两地间的路程是:
=1200(千米)
货车每小时行40千米,它行全程2/5的路程所用的时间和客车行全程3/5所用的时间是相同的,即两车同时出发相向而行至相遇时所用的时间。
=480÷40
=12(小时)
=720÷12
=60(千米)
也可以这样想:根据已知货车行了全程的3/5用了18小时,可以求出它行全程要用几小时。
所以客车的速度是:
40×1.5=60(千米)
还可以这样想:客车、货车同时从甲、乙两地出发到相遇,它们行驶的时间是相同的,因此客车、货车行驶的路程比就是客、货两车的速度比。所以客车的速度是:
答:客车每小时行60千米。
例74 一辆汽车运一批货从江城到海乡,又从海乡运一批货返回江城,往返共用了13.5小时。去时用的时间是回来时用的时间的1.25倍,去时的速度比返回时的速度每小时慢6千米。这辆汽车往返共行了多少千米?
分析与解 已知这辆汽车往返共用13.5小时,去时用的时间是回来时用的时间的1.25倍,即往返时间比是1.25:1,即5∶4。显然去时用的时间是:
=7.5(小时)
因为往返的路程是相等的,往返时间比是5∶4,那么往返的速度比就是4∶5。已知去时比回来时每小时慢6千米,于是可以求出去时的速度是:
6÷(5-4)×4
=6÷1×4
=24(千米)
这样又能求出这辆汽车往返的路程。这辆汽车往返共行了
24×7.5×2= 360(千米)
答:这辆汽车往返共行了360千米。
例75 甲、乙两辆汽车同时从A、B两地出发相向而行,第一次相遇地点离A地100千米,相遇后两车仍以原速继续行驶,分别到达B、A两地后,立刻沿原路返回,这时又在距B地60千米处相遇。求A、B两地间的距离。
分析与解 根据题中条件,可列方程解答。设A、B两地间的距离为x千米。两车速度是不变的,因此两车从出发到第一次相遇时所行路程比与从出发到第二次相遇时所行路程比是相等的,于是列方程得
200x-6000=x2-40x-6000
x2-240x=0
x(x-240)=0
x=240
这里列的方程是正确的,但小学生还不会解这个方程。
要是按如下思路来思考问题,那么,问题就可迎刃而解了。
甲、乙两车同时从A、B两地出发相向而行,到第一次相遇,两车共行了一个A到B的全程,其中甲车行了100千米。两车从A、B出发到第二次相遇,两车共行了3个A到B的全程,因此甲车行了3个100千米,这时离开B地60千米,因此,A、B间的距离是
100×3-60=240(千米)
答:A、B两地间的距离是240千米。
例76 一条小河流过A、B、C三镇。 A、B两镇之间有汽船来往,汽船在静水中的速度为每小时11千米。B、C两镇之间有木船摆渡,木船在静水中的速度为每小时3.5千米。已知A、C两镇水路相距50千米,水流速度为每小时1.5千米。某人从A镇上船,顺流而下到B镇,吃午饭用去1小时,接着乘木船又顺流而下到C镇。从A镇到C镇前后共用了8小时,那么A、B两镇间相距多少千米?
分析与解 由已知可得:汽船顺水每小时航行
11+1.5=12.5(千米)
木船顺水每小时航行
3.5+1.5=5(千米)
根据题意,两船航行共用了
8-1=7(小时)
假定从A镇到B镇也用木船摆渡,那么木船行了7小时共行
5×7=35(千米)
即少行了50-35=15(千米)
这是由于木船的速度比汽船慢的缘故。由此可求得汽船从A镇航行到B镇所用的时间为
15÷(12.5-5)=2(小时)
A、B两镇之间的距离为
12.5×2=25(千米)
答:A、B两镇之间相距25千米。
例77 小明骑自行车,从A地去B地,小华步行从B地去A地,二人同时出发相向而行,途中在C地相遇。相遇后小明又过15分钟到达B地,而小华却用了1小时到达A地,那么小明骑车与小华步行的速度比是几比几?
分析与解 根据题中给出的条件可知,小明骑车从A到C所用时间与小华步行从B到C所用时间相等。假设他们用的时间为x小时。
题中又告诉我们,小明从C到B所用的时间为15分钟,即1/4小时;小华从C到A所用的时间为1小时,而小明与小华行同样长的路程所用时间的
答:小明骑车与小华步行的速度比为2∶1。
例78 下图A、B、C是三个站,B到A、C两站的距离相等。小明和小强分别从A、C两站同时出发相向而行。小明过B站100米后与小强相遇。然后二人继续前进。小明到达C站后,立即沿原路返回,经过B站后300米追上小强。那么A、C两站间的距离是多少米?
分析与解 已知A、B两站间的距离和B、C两站间的距离相等,设A、B(或B、C)间的距离为x米。
根据题意,小明、小强分别从A、C两站同时出发相向而行,第一次相遇时,小明行了(x+100)米;小强行了(x-100)米。二人同时出发相向而行到第一次相遇,再到小明追上小强,小明行了(3x+30O)米,小强行了(x+300)米。
比较上面所得的结果不难发现,在同样多的时间里,小明行走(3x+30O)米的路程是他行走(x+100)米路程的3倍,那么小强行走的(x+300)米的路程也是小强行走(x-100)米路程的3倍,即
3(x-100)=x+300
3x-300=x+300
2x=600
即A、C两站间的距离是600米。
答:A、C两站间的距离是600米。
例79 某市20路公共汽车往返于甲、乙两地。甲、乙两地都按间隔相同的时间发一辆车。一个骑自行车的人按不变的速度向前行走,每隔15分钟有一辆公共汽车从背后开过,每隔10分钟有一辆公共汽车迎面驶来。问某市20路公共汽车每隔多少分钟分别从甲、乙两地发一辆车?
分析与解 根据题意,由于汽车每隔一定时间发一辆车,所以每相邻的两辆公共汽车之间的距离是相等的。假设每相邻的两辆公共汽车之间的距离
这12分钟就是汽车发车间隔的时间。
答:公共汽车每隔12分钟分别从甲、乙两地发一辆车。
例80 一个步行人和一个骑车人沿同一条公共汽车线路同向而行。骑车人的速度是步行人速度的3倍。每隔10分钟有一辆公共汽车超过步行人,每隔20分钟有一辆公共汽车超过骑车人。如果从始发站每隔同样的时间发一辆公共汽车,那么发车的间隔时间是多少?
分析与解 设每隔x分钟发一辆公共汽车。由题意可知,步行人走10分钟的路,公共汽车要行(10-x)分钟;骑车人行20分钟的路,公共汽车要行(20-x)分钟。
题中告诉我们,骑车人的速度是步行人的速度的3倍,因此,步行人所用时间与公共汽车所用时间的比的比值是骑车人所用时间与公共汽车所用时间的比的比值的3倍。
解方程得10×(20-x)=(10-x)×20×3
200-10x=600-60x
50x=400
x=8
也可以这样思考:
假设步行人走10分钟的路程为1。
因为骑车人的速度是步行人速度的3倍,所以骑车人行10分钟的路程为3,骑车人行20分钟的路程为6。
题中告诉我们,从始发站每隔同样时间发一辆公共汽车,所以在行走中两辆汽车的距离是相同的。已知每隔10分钟有一辆公共汽车超过步行人,每隔20分钟有一辆公共汽车超过骑车人。由此得出,汽车在10分钟所行的路程是(汽车间隔+1),而汽车在20分钟所行的路程则是(汽车间隔+6),所以汽车在10分钟所行的路程等于(6-1)。由此可见,汽车在10分钟所行的路程是步行人在10分钟所行路程的(6-1)÷1=5倍,那么汽车行驶步行人在10分钟内所行的路程,只要10÷5=2分钟就可以了。
因为每隔10分钟有一辆公共汽车超过步行人,所以公共汽车站发车的间隔是10-2=8分钟。
答:每隔8分钟发一辆公共汽车。
例81 张、王二人同时从A地去108千米外的B地。张先乘车,行一段路后下车改为步行,直达B地。王先步行,当与张乘坐的车返回A地途中相遇时,立即改为乘车向B地驶去。结果张、王二人同时到达B地。已知二人步行速度都是每小时行6千米,汽车每小时行36千米。问张是在离开A地多少千米处下车的?
分析与解 题中告诉我们,张先乘车后步行,王先步行后乘车,二人同时从A地出发又同时到达B地,这说明张、王二人步行的路程和乘车的路程分别相等。又知道二人步行的速度都是每小时行6千米,汽车每小时行36千米,因此,在相同的时间里,汽车行驶的路程是步行路程的36÷6=6倍。
根据已知,张、王二人步行和乘车的情况如下图所示。
根据前面分析可知,从A到C再到D的路程是AD间路程的6倍,所以从A到C的路程是AD间路程的(6+1)÷2=3.5倍。而A、D间的路程与C、B间的路程相等,因此A、B间的路程是C、B间路程的3.5+1=4.5倍。已知A、B间的路程是108千米,所以 C、B间的路程是 108÷4.5=24千米。由此得出,A、C间的路程是108-24=84千米,即张是在离开A地84千米处下车的。
也可以列方程求解。
设A、D间的路程为x千米,当然C、B间的路程也是x千米,那么从
9x=216
x=24
A、C间的路程为108-24=84(千米)
答:张是在离开A地84千米处下车的。
例82 有两个班的小学生要到少年宫参加活动,但只有一辆车接送。第1班的学生坐车从学校出发,第2班的学生同时开始步行。车到途中某处,让第1班学生下车步行,车立刻返回接第2班学生上车并直接开往少年宫。学生步行速度为每小时4千米,载学生时车速每小时40千米,空车每小时50千米。问要使两批学生同时到达少年宫,第1班学生步行了全程的几分之几(学生上下车时间不计)?
分析与解 根据题意,先把题中数量关系用图53表示出来。
要使两班学生同时从学校出发,并且同时到达少年宫,那么,这两班学生乘车和步行的路程必须分别相等,即AB=C′D,AC′=BD。
已知载学生时车速为每小时40千米,学生步行速度为每小时4千米,所以两班学生同时从学校出发到第1班学生下车时,乘车行驶的路程AB正好是
第1班学生下车后,汽车立即返回去接第2班学生,返回时车速为每小时
于是求出第2班学生又步行的路程B′C′相当于已步行的路程AB′的
这样进一步求出第2班从出发到乘车,即步行的路程
那么第1班步行了全程的
还可以列方程解答。
设从出发到第1班学生下车行了m小时,汽车立即返回到接第2班学生上车又行了n小时,这时汽车行了(40m+50n)千米,步行行了(4m+4n)千米。于是列方程,得
40m-4m-4n=50n
36m=54n
步行路程占全程的
答:第1班学生步行了全程的1/7。
例83 A、B两地间有一条公路。小明骑自行车从A地出发去B地,同时小华骑摩托车从B地去A地,60分钟后二人第一次相遇。相遇后二人继续前进,小华到达A地后立即返回,第一次相遇后又过了20分钟追上小明。小华到B地后又马上返回,这样一直下去,直到小明到达B地为止。小华从A地骑摩托车到B地的途中,共追上小明多少次?
分析与解
设C地为小明与小华第一次相遇的地方,D地为二人第一次相遇后,小华从A地骑摩托车返回B地途中,第一次追上小华的地方(如图54)。
由题意可知,小明从A到C骑自行车用了60分钟。再从C到D又骑行了20分钟。因为60÷20=3,所以A、C间的路程是C、D间路程的3倍。
二人第一次相遇后,小明骑自行车的路程是CD,而小华骑摩托车从C到A,再从A到D追上小明,共行了2个A、C间的路程与一个C、D间路程,即C、D间路程的3×2+1=7倍。因此得出,小华骑摩托车的速度是小明骑自行车速度的7倍。
小明从A地到B地,骑自行车行了1个A、B间的全程,小华骑摩托车则行了7个A、B间的全程。在这7个A、B间的路程中,有4次是从B地到A地,有3次是从A地到B地的。小华每行1个从A到B的全程,必然追上小明1次,因此,小华骑摩托车从A地到B地的途中,共追上小明3次。
答:小华骑摩托车从A地到B地的途中,共追上小明3次。
应用题部分练习
1.小明看一本书,原计划每天看35页,32天看完。实际每天比计划多看5页,实际用多少天看完?
2.修一条路,原计划每天修0.4千米,70天可以修完。实际每天修的米数是计划的1.25倍。实际用多少天完成?
3.绿化队植树,计划8天完成任务。实际每天植树240棵,7天就完成了全部的植树任务。实际比计划每天多植树多少棵?
4.某街道居委会慰问军烈属,给他们送去红糖和白糖。每到一户送去2袋红糖和5袋白糖,送到最后一户时,红糖正好送完,还剩下10袋白糖。已知带去的白糖的袋数是红糖袋数的3倍,那么带去的红糖、白糖各多少袋?
5.服装厂要加工一批服装。第一车间和第二车间同时加工60天正好完成。已知第一车间加工的服装占服装总数的45%,第二车间每天加工132件。第一车间每天加工多少件?
6.洗衣机厂计划生产一批洗衣机。结果9天恰好完成了计划的37.5%。照这样计算,完成计划还要多少天?
7.有一堆煤可以烧120天。由于改进烧煤技术,每天节约用煤0.25吨,结果这堆煤烧了150天。这堆煤共有多少吨?
牵走7头黄牛放在水牛群之中,那么这三群牛的头数正好相等。问奶牛有多少头?
9.甲乙两个车间加工一批同样的零件。如果甲车间先加工35个,然后乙
先加工1天,然后乙车间再开始加工,经过5天后两车间加工的零件数相等。那么乙车间一天加工多少个零件?
10.修路队原计划用240天修好一条长 91200米的公路。实际每天比计
12.有100千克青草,含水量为66%,晾晒后含水量降到15%。这些青草晾晒后重多少千克?
13.将一个正方形的一边减少1/5,另一边增加 4米,得到一个长方形。这个长方形与原来正方形面积相等。那么正方形面积有多少平方米?
14.某车间加工甲、乙两种零件。已加工好的零件中甲种零件占30%,后来又加工好了24个乙种零件,这时甲种零件占25%。那么现在已加工好两种零件共多少个?
15.甲、乙、丙三人共生产零件1760个。如果甲少生产2/9,乙多生产80个,那么甲、乙、丙三人生产零件的个数相等。甲、乙、丙三人各生产了多少个?
16.小明今年的年龄是他爸爸年龄的1/6,15年后他的年龄是他爸爸年龄的4/9。小明和他爸爸今年各多少岁?
17.某校有学生314人,其中男生人数的2/3比女生人数的4/5少40人。这个学校男生、女生各多少人?
18.甲、乙两班人数相等,各有一些同学参加了数学小组。甲班参加数学小组的人数恰好是乙班没参加数学小组人数的1/3;乙班参加数学小组的人数恰好是甲班没参加数学小组人数的1/4。那么甲班没参加数学小组的人数是乙班没参加数学小组人数的几分之几?
19.容器里放着某种浓度的酒精溶液若干升,加 1升水后纯酒精含量为25%;再加1升纯酒精,容器里纯酒精含量为40%。那么原来容器里的酒精溶液共几升?浓度为百分之几?
20.甲、乙、丙三人合抄一份稿件,1小时可以完成。如果甲、乙二人合抄,要80分钟完成;如果乙、丙二人合抄,要100分钟完成。如果这份稿件由乙一人独抄,要几小时完成?
21.一件工程,甲独做,20天可以完成;乙独做,30天可以完成。现在两人合做,中间甲休息了3天,乙休息了若干天,结果经过16天才完成。问乙休息了几天?
22.注满一池水,只打开甲管,要8小时;只打开乙管,要12小时;只打开丙管,要15小时。今开始只打开甲、乙两管,中途关掉甲、乙两管,然后打开丙管,前后共用了10小时才注满一池水。那么打开丙管注水几小时?
23.某工程队承建一项工程,要用12天完成。如果只让其中的甲、乙两个小队交换一下工作内容,那么全工程就要推迟3天完成;如果让其中甲、乙两个小队交换一下工作内容的同时,也让丙、丁两个小队交换工作内容,仍然可以按期完成全工程。如果只让丙、丁两个小队交换工作内容,那么可以使全工程提前几天完成?
24.甲、乙两队合干一项工程,甲队先独干了6天后,乙队参加和甲队一起干,又过了4天完成了全工程的1/3。又过了10天正好完成了全工程的3/4。因甲队另有任务调出,乙队继续工作,直到完成全工程。从开始到完工用了多少天?
25.甲、乙二人同时从A、B两地出发,各自去B、A两地,二人速度比为7∶6。二人相遇后继续向前行进,这时乙的速度比原来速度每小时增加
来的速度。
26.平日A、B两车分别从甲城、乙城两地同时出发,相向而行,6小时相遇。某日A车途中发生故障,修理占去了2.5小时,结果经过7.5小时两车才相遇。那么这一天A车从甲城出发到乙城用了多少小时?
27.某市104路电车起点站和终点站都按一定的间隔时间发一辆电车,并且匀速行驶。张华骑车沿104路电车线以均匀速度行驶,每隔12分钟有一辆电车从后面超过他,每隔4分钟有辆电车迎面开来。那么104路电车起点站和终点站每隔多少分钟发一辆车?
28.甲、乙二人步行的速度比为11∶7。二人分别从A、B两地相向而行,2小时相遇。如果二人同向而行,几小时后甲追上乙?
29.45名学生要到离学校30千米的郊外劳动。学校只有一辆汽车能乘坐15人,汽车的速度是每小时60千米。学生步行的速度是每小时4千米。为使他们尽早到达劳动地点,他们最少要用几小时才能全部到达?
30.甲、乙两班学生同时从学校出发去少年宫。甲班步行的速度是每小时5千米,乙班步行的速度是每小时6千米。学校有一辆汽车恰好可以坐一个班的学生,汽车每小时行30千米。为了使两班学生尽早到达少年宫,甲、乙两班步行路程比应该是几比几?
31.一辆汽车从甲地开往乙地。如果把车速度提高20%,那么可以比原定时间提早1小时到达。如果以原速行驶120千米后,再将速度提高25%,那么可以比原定时间提早40分钟到达。甲、乙两地之间的路程有多少千米?
32.从甲市到乙市有一条公路,它分成三段,其中第一段长是第三段长的2倍。在第一段路上,汽车的速度都是每小时40千米;在第二段路上,汽车的速度都是每小时90千米;在第三段路上,汽车的速度都是每小时50千米。现有两辆汽车同时从甲、乙两市出发相向而行,1小时20分后在第二段路的1/3(从甲市到乙市方向的1/3)处相遇。那么甲、乙两市相距多少千米?
33.甲、乙两车同时从A地出发到B地。甲车按原定速度行了全程的2/3后,车速提高了1倍,结果比原计划时间提前2小时到达B地;乙车按每小时30千米的原定速度行了全程的1/4后,车速提高了1倍,结果两车同时到达B地。那么甲原定每小时行多少千米?
34.甲、乙两城之间有长途汽车以固定速度行驶。如果车速比原定速度每小时快6千米,那么就可以早到20分钟。如果车速比原定速度每小时慢5千米,那么就要迟到24分钟。问甲、乙两城间的路程是多少千米?
35.甲、乙、丙三人进行自行车比赛,结果甲比乙早24分钟、乙比丙早6分钟到达终点。又知道甲速度比乙速度每小时快5千米,乙速度比丙速度每小时快1千米。甲、乙、丙三人比赛的路程有多少千米?
杂题部分
小学生的课外数学活动,包括一些数学竞赛活动,极大地提高了小学生学习数学的兴趣和热情。通过参加各种数学课外活动,提高了学生思维和探索能力。杂题中选编的例题,更突出了小学数学知识的综合运用。有的题涉及一点小学尚未学习的知识,但是学生还是可以理解的,题中介绍的各种解法,小学生应该掌握。
例84 将奇数1、3、5、7、9、……按下表排成五列。
例如,13排在第2行第2列,25排在第4行第4列。那么1993排在第几行第几列?
分析与解 首先要算出1993这个数是这列数中的第几个数。
由上表可看出,每行有4个数,而997÷4=249……1。就是说第997个数是第250行中最小的一个。偶数行的数是从小到大依次排在第4、3、2、1列的,因此1993这个数排在第250行第 4列。
例85 在自然数中有很多三位数,其中三个数字之和是5的倍数的三位数共有多少个?
分析与解 要想求出三个数字之和是5的倍数的三位数共有多少个,不妨按从小到大的顺序把这些数写出来:104、109、113、118、122、127、……显然,用这种寻找答案的方法是可以的,但是太费时间了。
我们可以按下面的思路去思考。
这10个连续的三位数的三个数字之和,也正好是10个连续的自然数。例如,A=1,B=2,那么上面写出的10个连续的三位数的三个数字之和为3、4、5、6、7、8、9、10、11、12。其中有而且只有两个三位数的三个数字之和是5的倍数。
从100~999,这些三位数共900个,每10个连续三位数为一个“数段”,一共可以分成90个“数段”。而每10个连续的三位数中有而且只有2个三位数的三个数字之和是5的倍数,所以在所有的三位数中共有 2×90=180个三位数,它们的三个数字和是5的倍数。
答:三位数中三个数字之和是5的倍数的共有180个。
例86 有一串数 1、4、9、16、25、26、49、……它们是按一定的规律排列的。那么左起第1994个数比第1993个数大多少?
分析与解 仔细观察这串数各数的特征不难发现,这串数是从1开始的自然数的平方数,即12、22、32、42、52、62、72、……
进而比较相邻两数之差,可以发现
4-1=22-12=2+1
9-4=32-22=3+2
16-9=42-32=4+3
25-16=52-42=5+4
由此可以推得,左起第1994个数比第1993个数大
1994+1993=3987
答:左起第1994个数比第1993个数大3987。
例87 有一列数 1、2、4、7、11、16、22、29、……这列数左起第1994个数除以5的余数是多少?
分析与解 观察这一列数,我们发现它排列的规律是:第2个数比第1个数多1;第3个数比第2个数多2;第4个数比第3个数多3;……依次类推。这样我们就可以先求出第1994个数是几,再算出这个数除以5的余数是多少了。
左起第1994个数是
1+1+2+3+…+1993
=1+1987021
=1987022
再计算1987022除以5的余数,得到余数是2。
也可以这样思考:
根据这列数排列的规律,我们先列出前15个数,然后再算一下这15个数被5除的余数。列表如下:
从上表可以看出、第1、2、3、4、5五个数被5除的余数,与第6、7、8、9、10五个数被5除的余数对应相同、也与第11、12、13、14、15五个数被5除的余数对应相同。由此得出,这一列数被5除的余数,每隔5个数循环出现。
因为1994=5×398+4,所以第1994个数被5除得到的余数,与第四个数除以5得到的余数一样,也就是余数为2。
答:这列数左起第1994个数除以5得到的余数是2。
例88 有1994名同学按编号从小到大排成一排,令奇数号位(1号位、3号位……)上的学生离队。余下的同学顺序不变,再令其中站在新编号为奇数号位上的同学离队。依次重复上面的做法,那么最后留下来的同学,在开始时是排在第几号位上的?
分析与解 依照题中所说的做法,第一次令奇数号位上的同学离队后,余下的同学,开始时编号是2(21×1)、4(21×2)、6(21×3)、……、1994(21×997),再令余下的同学中站在奇数号位上的同学离队后,剩下的同学开始时的编号是4(22×1)、8(22×2)、12(22×3)、16(22×4)、……、1992(22×498)
依次类推,第9次令余下的同学中站在奇数号位上的同学离队后,剩下的同学开始时的编号是29×1,29×2,29×3。
第10次令余下的同学中站在奇数号位上的同学离队后,只剩下一个同学,他开始时的编号是:210×1,即1024。
答:最后留下来的同学,在开始时是排在第1024号位上的。
例89 把乒乓球装在6个盒中,每盒装的个数分别为1个、3个、9个、27个、8l个、243个。从这6盒中,每次取其中1盒,或取其中几盒,计算乒乓球的个数之和,可以得到63个不同的和。如果把这些和从小到大依次排列起来,是1个、3个、4个、9个、10个、12个、……,那么第60个和是多少个?
分析与解 首先应该想到,不能用从取1盒、取2盒、……去计算乒乓球个数之和的办法,去寻找第60个和是多少个。根据题意,第63个兵乓球个数之和是很容易计算出来的,而第60个兵乓球个数之和与它相差不多,例推回去,就可以得出结果了。
根据已知,第63个乒乓个数之和是
1+3+9+27+81+243=364
于是第62个乒乓球个数之和应该是
364-1=363
第61个乒乓球个数之和应该是
364-3=361.
第60个乒乓球个数之和应该是
364-3-1=360
答:第60个乒乓球个数之和是360。
例90 有甲、乙、丙、丁四个人,他们的年龄一个比一个大2岁,这四个人年龄的乘积是48384。这四个人的年龄各是几岁?
分析与解 题中告诉我们,48384是四个人年龄的乘积,只要我们把48384分解质因数,再按照每组相差2来分成四个数相乘,这四个数就是四个人的年龄了。
48384=28×33×7
=(22×3)×(2×7)×24×(2×32)
=12×14×16×18
由此得出这四个人的年龄分别是12岁、14岁、16岁、18岁。
也可以这样想:
由题意可知,这四个数是相差2的四个整数。它们的积是偶数,当然这四个数不是奇数,一定是偶数。又因为48384的个位数字不是0,显然这四个数中,没有个位数字是0的,那么这四个数的个位数字一定是2、4、6、8。
又因为104<48384,而 48384<204,所以可以断定,这四个数一定是12、14、16、18。也就是说,这四个人的年龄分别是12岁、14岁、16岁、18岁。
答:这四个人的年龄分别是12岁、14岁、16岁、18岁。
例91 把分母为60的最简假分数从小到大排列,第1994个分数是几分之几?
分析与解 直接求出第1994个假分数是几分之几,是不大容易的。我们不妨换一下思考的角度,那就是将假分数化成带分数去思考,求出第1994个带分数是几又几分之几,再把这个带分数化成假分数就可以了。
由于分母是60的最简真分数共有16个,把它们从小到大排列起来,依
由此可知,分母为60的最简假分数化成带分数后,由小到大依次排列,
因为1994÷16=124……10,所以第1994个带分数的整数部分是
答:第1994个最简假分数是7537/60。
例92 有 A、B、C、D、E五个小足球队参加足球比赛,到现在为止,A队赛了4场,B队赛了3场,C队赛了2场,D队赛了1场。那么E队赛了几场?
分析与解 把参赛的五个球队看成平面上不在同一条直线上的五个点,并且没有3个点在一条直线上。这样每两队比赛了1场,就可以用相应的两点间连一条线段来表示。根据各队比赛过的场次可画成图55。
从上图不难看出,E队赛了2场。
答:E队赛了2场。
例93 有4个不同的自然数a、b、c、d,而且a<b<c<d。又知道a比b小5,d比c大7,这四个数的平均数是 17,那么d最大是多少?最小是多少?
分析与解 题中告诉我们,四个数的平均数是17,那么这四个数的和就是17×4=68。
题中问d最大是多少。要使d最大,那么a就要尽量小。因为这四个数都是自然数,所以a最小为1。又因为a比b小5,所以这时b为6。这样不难求出这时c与d的和是68-1-6=61。题中又告诉我们,d比c大7,这样就可以求出这时d是61+7/2=34,即d最大是34。
那么d最小是多少呢?
题中告诉我们,a比b小5,d比c大7,a、b、c、d四个数之和是68,而68+5+7之和正好是b与d的和的2倍,因此b与d的和是(68+5+7)÷2=40。要使d最小,那么a、b、c就要尽量大,而b与c的差应该尽量小,而b与c的差最小是1,这样b与d之差就是1+7=8。由此得出d最小是:40+8/2=24
答:d最大是34,最小是24。
例94 一个正方体有六个面,分别用字母A、B、C、D、E、F表示。图56是从三个不同角度看到的这个正方体的部分面的字母。那么这个正方体到底哪个面与哪个面相对?
分析与解 观察题中给出的三个图,不容易看出哪个面与哪个面相对。那就换一种思考方法,看看哪个面不对着哪个面,从而得出哪个面与哪个面相对的正确结论。
观察图(1)可知,A面不对着D面、E面;观察图(2)可知,A面不对着B面、F面。由此得出,A面一定对着C面。
再观察图(2),可以知道,F面不对着A面、B面;观察(3)可以知道,F面不对着C面、D面。那么F面一定对着E面。
这样剩下的B面一定对着D面。
答:这个正方体的A面对着C面;B面对着D面;E面对着F面。
例95 一次乒乓球比赛,共有512名乒乓球运动员参加比赛。比赛采用淘汰制赛法,两个人赛一场,失败者被淘汰,将不再参加比赛;获胜者进入下轮比赛,如此进行下去,直到决赛出第一名为止。问这次乒乓球比赛一共要比赛多少场?
分析与解 如果这样去想,第一轮512名运动员参赛,要赛256场;第二轮256名运动员参赛,要赛128场;……直到决赛出第一名为止,再将各轮比赛场次加起来,计算出一共要比赛多少场。这种方法是可以的,不过太复杂了。
如果按下面的思路思考,那就简单得多了。
根据题中所说,比赛采取淘汰制,每比赛一场淘汰掉1人,到最后决赛得出第一名,只有这第一名未被淘汰。也就是说,512名运动员参赛,有511人被淘汰。淘汰一个人就要赛一场,所以这次乒乓球比赛一共要进行511场比赛。
答:这次乒乓球比赛,一共要比赛 511场。
例96 一只杯子里装着红葡萄酒,一只杯子里装着白酒,都是300毫升。现在从装着红葡萄酒的杯中倒出30毫升红葡萄酒与白酒混合,混合均匀后,再从混合的酒中取出30毫升倒回装红葡萄酒的杯中,每个杯中的酒仍然是300毫升。问这时是红葡萄酒杯中的白酒多呢?还是白酒杯中的红葡萄酒多呢?
分析与解 解答这题不应从具体数量上分析入手,因为那样计算就太复杂了。
根据题中条件,红葡萄酒和白酒的数量都是300毫升,我们用V表示。白酒中红葡萄酒的含量用a表示,红葡萄酒中白酒的含量用b表示。于是白酒杯中的酒是
V=(V-b)+a
红葡萄酒杯中的酒是
V=(V-a)+b
因此,(V-b)+a=(V-a)+b
那么 a-b=b-a
2a=2b
所以 a=b
这就是说,白酒里的红葡萄酒与红葡萄酒里的白酒是一样多的。
当然题目还可以改为:“不等混合均匀,又倒回30毫升”,那该是怎样的结果呢?
这个问题的回答是:结果与前面完全一样,其中的道理也就不用再说了。
答:红葡萄酒中的白酒与白酒中的红葡萄酒一样多。
例97 甲盒中有1993个白棋子和1994个黑棋子,乙盒中有足够多的黑棋子。现在每次从甲盒中任取2个棋子放在外面。如果被取出的2个棋子是同颜色的,就从乙盒中取1个黑棋子放入甲盒;如果取出的2个棋子是不同颜色的,便将那个白棋子再放回到甲盒中去。这样经过3985次取、放之后,甲盒中还剩下几个棋子?它们是什么颜色的?
分析与解 根据题意,甲盒中共有1993+1994= 3987(个)棋子。每次取出2个棋子后又放回到甲盒中1个棋子,实际每次取、放后,甲盒中减少1个棋子。因此,经过3985次取、放后,甲盒中还剩下3987-3985=2个棋子。
根据题中所说的取、放方法,每次取、放之后,甲盒中要么减少1个黑棋子,要么减少2个白棋子增加1个黑棋子。显然,甲盒中的白棋子总是两个两个地减少。而甲盒中有1993个白棋子,那么,最后必定剩下1个白棋子。另外剩下的那个棋子一定是黑色的。
答:甲盒中还剩下2个棋子,1个白色的,1个黑色的。
例98 某市电话403局的各户电话号码是4030000~4039999。那么除局号外其余4个数码中的前两个数码之和与后两个数码之和不相等的电话号码共有多少个?
分析与解 我们知道,403局的电话号码0000~9999,共有10000个号码。而前两个数码之和与后两个数码之和相等的号码的个数,比前两个数码之和与后两个数码之和不相等的号码的个数少得多。因此,要求前两个数码之和与后两个数码之和不相等的电话号码的个数,应该先求出前两个数码之和与后两个数码之和相等的个数,再从 10000中减去这个数,所得的结果就是题目所要求的电话号码的个数了。
那么除局号外,在其余4个数码中,前两个数码之和与后两个数码之和相等的号码有多少个呢?
我们知道,在这些号码中,两个号码之和最小的是0,最大的是18。
前、后两个数码之和为0的,只用到数字0,即0000。前、后两个数码之和为18的,只用到数字9,即9999。显然,前、后两个数码之和为0或18的,都只用到1个数字,各有1个号码。
再看前、后两个数码之和为1的情况。这时只用到0和1两个数字,它们是0101、0110、1010、1001,共4个号码。前、后两个数码之和为17的,只用到8和9两个数字,它们是
8989、8998、9898、9889,共4个号码。显然,前、后两个数码之和为1或17的,都用到2个数字,各有4个号码。
我们再看看前、后两个数码之和为2的情况。这时只用到0、1、2三个数字,它们是0202、0220、2020、2002、1102、0211、2011、1120、1111,共9个号码。前、后两个数码之和为16的,用到 7、8、9三个数字,它们是7979、7997、9797、9779、8879、7988、8897、9788、8888,共9个号码。显然,前、后两个数码之和为2或16的,都用到3个数字,各有9个号码。
从以上列举的三种情况看,我们发现,前、后两个数码之和相等的号码,如果用到1个数字,就有1个号码,即12个;用到2个数字,就有4个号码,即22;用到3个数字,就有9个号码,即32个。
前面已经说了,前、后两个数码之和最小的是0,最大的是18,共有19种情况。我们把这19种情况,即用到数字的个数及号码的数,列成下表。
从上表不难看出,前两个数码之和与后两个数之和相等的号码共有
(12+22+32+42+52+62+72+82+92)×2+102
=(1+4+9+16+25+36+49+64+81)×2+100
=285×2+100
=570+100
=670(个)
于是得出,除局号外,在其余的四个数码中,前两个数码之和与后两个数码之和不相等的电话号码共有
10000-670=9330(个)
答:前两个数码之和与后两个数码之和不相等的电话号码共有 9330个。
例99 用红、黄、蓝三种颜色把图57中8个圆圈涂上颜色,每个圆圈只许涂一种颜色,并且有连线的两端的圆圈不能涂上相同的颜色,那么共有多少种不同的涂法?
分析与解 根据题中条件,首先要想到中间菱形的四个圆圈连线最多,应该从这里开始思考。为了说明方便,先用字母表示图中各圆圈,如图58所示。
假如在A圆圈内涂红色,那么B、C、D三个圆圈的涂色方法有六种,如图59所示。
因为A圆圈可以涂红、黄、蓝三种颜色,所以A、B、C、D四个圆圈的涂色方法共6×3=18种。
又因为A、B、C、D都有一条线分别与E、F、G、H相连,所以 E、F、 G、H各有2种不同的涂法,由此共有18×2×2×2×2=288种不同的涂法。
答:共有288种不同的涂法。
例100 9月1日开学那天,五年级数学科代表向李老师汇报说:“李老师,我们100个同学,在暑假里一共做了1600道数学题。”李老师听了非常高兴,当即表扬了他们,并且说:“你们100个人中,至少有4个人做的数学题的数目一样多。”李老师说的这句话对吗?为什么?
分析与解 根据题意,把100个学生按3人为一组,分成33组,还剩下1个学生。
假设第1组3个学生都没做题,即每人做了0道题;第2组3个学生每人做1道题;第3组3个学生每人做2道题;…… 第33组3个学生每人做32道题。剩下的一个学生要是与前面的99个学生做的题数不相同,最少也要做33道题。这样100个学生最少共做了
3×(0+1+2+3+4+…+31+32)+33
=3×528+33
=1584+33
=1617(道)
超过了1600道题。要是不超过1600道题,必须有1个或更多的学生少做题,合起来共少做了17道题。其实只要有1个学生少做了题,这个学生就会归到其它做题少的那组中去。这样一来,那个组就会有4个学生做题一样多了。
因此,李老师的话是正确的。
杂题部分练习。
1.明明和小华到新华书店去买《小学数学百问》这本书。一看书的价钱,发现明明带的钱缺1分钱,小华带的钱缺2.35元。两人把钱合起来,还是不够买一本的。那么买一本《小学数学百问》到底要花多少元?
2.将奇数按如下顺次排列
1 5 7 19 21
3 9 17 23 ……
11 15 25 ……
13 27 ……
29 33 ……
31 ……
在这样的排列中,17这个数排在第2行第3列,33这个数排在第5行和2列,那么1995这个数排在第几行第几列?
3.有一列数,第一个数和第二个数都是1994,以后每个数都是前面两个数的和,这列数的第1994个数除以3的余数是几?
4.11+22+33+44+55+66+77+88+99+1010除以3的余数是几?
5.某班有学生51人,准备推选1名同学在教师节那天给老师献花。选举的方法是让51名同学按编号1、2、3、……、51排成一个圆圈,从1号位开始,隔过1号,去掉2号、3号,隔过4号,去掉5号、6号……如此循环下去,总是每隔过1个人,就去掉2个人,最后剩下的那名同学当选。那么当选的同学开始时是排在几号位置上的?
6.设 1、3、9、27、81、243、729、2187是给定的 8个数,在这8个数中每次取1个或取几个不同的数求和,可以得到一个新数,这样共得到255个新数。从小到大把这些新数排列起来,那么第250个数是几?
7.有一列数1/1、1/2、2/2、1/2、1/3、2/3、3/3、2/3、1/3、1/4、2/4、3/4、……那么第398个数是多少?
8.下图中已填好了2个数6和7,再从1、2、3、4、5中选出4个数填在图中空格中,要使填好的格里的数右边比左边大,下边比上边大,那么一共有多少种不同的填法?
9.下面方格中每横行、每竖行、每条对角线上的三个数之和都相等,那么方格中的A、B、C、D、E各是多少?
10.有四包糖,每次选出其中的3包,算出这三包的平均重量,再加上另一包的重量,用这种方法算了4次,分别得到下面4种重量8.8千克,9.6千克,10.4千克,11.2千克那么这四包糖平均每包重多少千克?
小明摆了两次,第一次摆成正方阵后,余下12枚棋子;第二次摆成每边各加 1枚棋子的正方阵时,还缺少9枚棋子。那么这些棋子共有多少个?
12.有两列数,它们各自按一定的规律排列。第一列数是:3、5、7、9、……,第二列数是:4、9、14、19、24、……,第一列数中的第1个数与第二列数中的第1个数相加是3+4;第一列数中的第2个数与第二列数中的第2个数相加是5+9;……那么两列数第80个数相加,是几+几?
13.有7000多棵小树苗,按着六种规格捆成若干小捆。如果每10根捆成1捆,结果剩下9棵;如果每9棵捆成1捆,结果剩下8棵;第三、四、五、六种规格是:分别以8棵、7棵、6棵、5棵捆成1捆,那么最后分别剩下7棵、6棵、5棵、4棵。问一共有多少棵小树苗?
14.有几个长方形,它们的长和宽的长度都是小于10的自然数,并且各个长方形的宽与长的比值都比3/10大,比1/2小。那么这几个长方形的面积总和是多少?
15.有一个数比30小,它与2的差能被3整除。它与3的和能被4整除。它与1的和能被5除整除。这个数除以60的余数是几?
16.如果两个数的和是80,这两个数的积可以整除4875,那么这两个数的差是多少?
17.一个六位数,把它的末三位一起搬到前三位的前面,成为一个新的六位数,而原来那个六位数的7倍正好等于新的六位数的6倍。原来的六位数是多少?
18.某校六年级学生按一层男生、一层女生地排成一个正方阵。又知道男生比女多25人,这个学校的六年级共有多少学生?
19.在小于5000的自然数中,能被11整除,并且数字和为13的数,共有多少个?
20.有若干学生参加数学竞赛,每个学生的得分都是整数。已知参赛学生所得的总分是4729分,并且前三名的分数分别是88分、85分、80分,最低分是30分,又知道没有与前三名得分相同的学生,其它任何一个分数,得到这个分数的都不超过3人。那么在这次竞赛中得分不低于60分的学生至少有多少名?
21.某班一次考试有52人参加,共考 5个题,每道题做错的人数如下:
又知道每人至少做对一道题,做对一道题的有7人,5道题全做对的有6人,做对2道题的人数和3道题的人数一样多,那么做对4道题的有多少人?
22.某车间原有工人不少于63名。在1月底以前的某一天调进了若干工人,以后每天都增调1人进车间工作。现在知道,这个车间在1月份每人每天生产1件产品,共生产了1994件。试问1月几号开始调进工人?共调进了多少工人?
23.打一份稿件,甲单独打,要6小时完成。如果按甲、乙、丙轮流每人打1小时的顺序去打,正好用整小时数完成;如果按乙、丙、甲轮流每人打1小时的顺序去打,就要比按甲、乙、丙轮流的顺序去打多用0.5小时完成;如果按丙、甲、乙轮流每人打1小时的顺序去打,就要比按甲、乙、丙轮流的顺序去打多用0.25小时完成。现在由甲、乙、丙合打这份稿件,需要几小时完成?
答案仅供参考:
1.明明买这本书还缺1分钱,小华要是能补上1分钱,就能买这本书了。可是小华、明明的钱合起来,仍然买不了这本书,这说明小华连1分钱也没带。
题中说,小华买这本书缺2.35元,那么2.35元正好是这本书的价钱了。
所以买一本《小学数学百问》要花2.35元。
个数是990×2—1=1979
排在第1行第45列的数是1981,1983是第2行第44列上的数,余类推,得出1995排在第8行第38列。
3.首先算出这一列数除以3的余数排列的规律。
从上表不难看出,这列数被3除的余数呈2、2、1、0、1、1、2、0这八个数一循环的排列,而1994÷8=249……2,即1994个数除以3的余数同第二个数除以3的余数一样,即余2。
4.因为3、6、9都能被3整除,因此33、66、99都能被3整除,即33、66、99除以3的余数都是0。
我们知道,一个不能被3整除的数的平方数被3除的余
数都是1,因此
11=12,12除以 3余数是1;
22除以3的余数是1;
44=4×4×4×4=(4×4)2,44除以3的余数是1;
88=8×8×8×8×8×8×8×8=(8×B×8×8)2,88除以3的余数是1;
1010=10×10×10×10×10×10×10×10×10×10=(10×10×10×10×10)2,1010除以3的余数是1。
再看一下55=5×5×5×5×5
= 5×5×5×5×(3+2)
=(5×5)2×(3+2)
=(5×5)2×3+(5×5)2×2
其中(5×5)2×3能被 3整除,(5×5)2×=1250, 1250除以 3的余数是2,因此55除以3的余数是2。
77=7×7×7×7×7×7×7
=(7×7×7)×(7×7×7)×(6+1)
=(7×7×7)2×(6+1)
=(7×7×7)2×6+(7×7×7)2×1
其中(7×7×7)2×6能被3整除,(7×7×7)2×1除以 3的余数是 1,因此7×7除以 3的余数是 1。
由以上分析,得出:
11、22、44、55、77、88、1010除以3的余数分别是1、1、1、2、1、1、1,这些余数的和是8,而8除以3的余数是2。因此,
11+22+33+44+55+66+77+88+99+1010除以3的余数是2。
5.根据推选的方法可知,第一轮筛选后留下了17人。这17人是排在第 1、4、7、10、13、16、19、22、25、28、31、34、37、40、43、46、49号位置上的同学。接下去继续筛选,留下了6人,这6个人是排在第1、10、19、28、37、46号位置上的同学。不过留下46号后去掉49号,接下来正好去掉1号,再继续下去,留下的是第10、37号位上的同学,在去掉46号之后,接下去是去掉10号,最后剩下的是37号,即开始时排在37号位置上的那个同学当选。
6.第255个数是:
1+3+9+27+81+243+729+2187=3280
第 250个数是:3280—1—9=3270
7.仔细观察这列分数的特点,不难发现,它们的分母是1、2、3、4.……分母是1的分数有1个;分母是2的分数有3个;分母是3的分数有5个;……分子是1、1、2、1、1、2、3、2、1……从小到大再到小,依次排列。从而得出,从第400个分数是分母为20的分数中最后一个,
8.当空格中取1、2、3、4时,有2种填法,即
1 2 1 3
3 4 2 4
当空格中取1、2、3、5时,有2种填法,即
1 2 1 3
3 5 2 5
当空格中取1、2、4、5时,有2种填法,即
1 2 1 4
4 5 2 5
当空格中取1、3、4、5时,有2种填法,即
1 3 1 4
4 5 3 5
当空格中取2、3、4、5时,有2种填法,即
2 3 2 4
4 5 3 5
由此得出,共有2+2+2+2+2=10种不同填法。
9.19+10+D=D+18+E
∴E=11
19+A+14=A+B+18
∴B=15
19+15+11=14+15+D
∴D=16
三数之和是19+10+16=45
∴A=45—19—14=12
C=45—14—11=20
10.根据题中所说的称重方法可知,每包糖重在四次的计算中,三次各取了每包的1/3,一次取了一包的重量,也就是说,这四次计算中,每包的重量都被计算了两次。因此,8.8+9.6+10.4+11.2的和相当于四包糖重的2倍,那么这四包糖平均每包的重量是:
=5(千克)
11.解法(1)根据题意,两次摆放棋子都要摆成正方阵,那么两次要摆成的正方阵所需要的棋子数一定是两个相邻的平方数,像22=4,32=9,4和9是两个相邻的平方数。
题中告诉我们,第一次摆成正方阵后,余下12枚棋子,第二次摆成正方阵时缺少9枚棋子,那么两次摆成正方阵后棋子数相差12+9=21枚。也就是说,两个相邻的平方数相差21。我们知道102=100,112=121,而121—100正好是21。
由此得出,这堆棋子共有
100+12=112(枚)
或121—9=112(枚)
解法(2)根据题意,第二次摆成的正方阵要比第一次摆成的正方阵多用了第一次摆成的正方形最外一层每边棋子数的2倍多1枚。题中告诉我们,第二次摆成正方阵还差9枚棋子,而第一次摆成正方阵后余下12枚,就是说,第二次摆成的正方阵由于多摆了一层而多用了12+9=21枚棋子,多用的棋子数比第一次摆成正方阵的最外一层每边的棋子数的2倍多1枚。
因此第一次摆成正方阵时,最外一层每边上的棋子数是:
(9+12—1)÷2=10(枚)
那么这些棋子数是:
10×10+12=112(枚)
或(10+1)×(10+1)-9=112(枚)
下面再用方程表示。
设第一次摆成正方阵时,最外一层的棋子数为x枚,则
2x+1=9+12
2x=9+12-1
2x=20
x=10
这些棋子共有10×10+12=112(枚)
或(10+1)×(10+1)-9=112(枚)
12.观察两列数排列的规律不难发现:第一列数是从3开始、公差为2的数列,因此第一列数的第 80个数是 3+ 2×(80—1)=161。第二列数是从4开始、公差为5的数列,因此第二列数的第 80个数是 4+5×(80—1)=399。
由此得出这两列数的第80个数相加是161+399。
13.5、6、7、8、9、10的最小公倍数是2520,它的3倍是7560,7560—1=7559(棵)
们的总和是133。
15.4×5+3×5×3+3×4×2—60=29
29除以60的余数是29。
16.4875=3×5×5×5×13
由此得出这两个数是:5与75或15与65。这两个数的差是 70或50。
由此得出,原来那个六位数是461538。
18.根据男生比女生多25人,可知方阵中心站1名男生,这个方阵共排
19.根据已知条件,符合要求的数不可能有一位数及两位数。在三位数及四位数中,奇、偶数位上数字和的差不可能是0,只能是11。
因此在三位数中,只有十位数字为1,个位与百位数字之和为12的一些数。于是得出符合要求的数有
319、913、418、814、517、715、616、共有7个数。
在四位数中有(3+9)-(1+0)=11、(4+8)-(1+0)=11、(5+7)-(1+0)=11、(6+6)-(1+0)=11。于是得出符合要求的数有
1309、1903、3091、3190、1408、1804、4081、4180、1507、1705、1606共11个数。
合起来共有7+11=18个小于5000的数,其数字和为13,并且能被11整除。
20.要求得分不低于60分的学生至少有多少人,那么不及格的人数应尽量多,得高分的也应尽量多。根据题意,不及格的学生最多占去的分数是:
(30+31+32+……+58+59)×3=4005(分)
除去不及格的及前三名学生的得分,还有
4729-4005-88-85-80=471(分)
再从这471分中依次去掉3个79分,3个78分,得
471-79×3-78×3=0(分)
这说明得79分的有3人,得78分的有3人。再加上前三名学生,共9人及格,这就是说,不低于60分的学生至少有9人。
21.根据已知,全班 52人应做对 5×52=260(道)题。实际做对 260-(4+6+10+20+39)=181(道)题。做对2道、3道、4道题的有52-7-6=39(人)。做对1道题及5道题的共做对1×7+5×6=37(道)题,那么做对2道、3道、4道题的39人共做对181-37=144(道)题。
题中告诉我们,做对2道、3道题的人数一样多,可以把他们看成做对了(2+3)÷2=2.5(道)题。
假设做对2道、3道、4道题的39人全做对了2.5道题,那么做对了4道题的有
(144—2.5×39)÷(4—2.5)=31(人)
22.根据题意可得1994=63×31+41
1994=64×31+10
而 1994<65×31,也就是说,这个车间原有工人63人或64人,于1月份可生产63×31=1953件产品或生产64×31=1984件产品,这样还差41件或10件产品未完成。
根据已知,应把41或10表示为若干连续自然数之和。我们知道,41=20+21,10=1+2+3+4,这就是说,1月30日开始调进20人,1月31日再增调1人,共调进21人。或1月28日开始调进1人,以后每天增调1人,到1月31日共调进4人。
23.根据题意可知,如果按甲、乙、丙、甲、乙、丙……丙最后完成的顺序去打,或按乙、丙、甲、乙、丙、甲……甲最后完成的顺序去打,或按丙、甲、乙、丙、甲、乙……乙最后完成的顺序去打,完成这份稿件都应是3小时的整倍数。但是题中告诉我们,如果按乙、丙、甲的顺序去打,要比按甲、乙、丙的顺序去打多用0.5小时完成;如果按丙、甲、乙的顺序去打,要比按甲、乙、丙的顺序去打多用0.25小时完成。由此可知,如按甲、乙、丙的顺序去打,最后完成这份稿件的不是丙,而是甲或乙。
如果是甲最后完成,那么完成全部稿件的方案如下:(脚码表示工作的小时数)
甲1 乙1 丙1 甲1 乙1 丙1……甲1
乙1 丙1 甲1 乙1 丙1 甲1……乙1丙0.5
丙1 甲1 乙1 丙1 甲1 乙1……丙1甲0.25
由以上三种方案可知,经若干轮后,余下的工作量,甲打1小时完成;或乙打1小时后,丙再打0.5小时完成;或丙打1小时后,甲再打0.25小时完成。由此得出:
打这份稿件,所用的时间是:
由上面得出的合打时间可知,甲、乙、丙各打2小时后,甲、乙、丙还
1小时完成相矛盾。这说明最后完成的是乙而不是甲。
由乙最后完成,那么完成全部稿件的方案如下:
甲1 乙1 丙1 甲1 乙1 丙1……甲1乙1
乙1 丙1 甲1 乙1 丙1 甲1……乙1丙1甲0.5
丙1 甲1 乙1 丙1 甲1 乙1……丙1甲1乙0.25
由以上方案可知,用、乙、丙经若干轮后,余下的工作甲打1小时,乙再打1小时完成;或乙打1小时、丙打1小时后,甲再打0.5小时完成;或丙打1小时、甲打1小时后,乙再打0.25小时完成。由此得出
进而求出甲、乙、丙的工效之和是:
甲、乙、丙合打这份稿件,需要
甲、乙、丙各打2小时后,余下的工作由甲先打1小时,再由乙打还要
 爱华网
爱华网


