在备课中有两个问题需要精心设计.一个是问题的引入,一个是定理的证明.课本通过一个实际问题引入,但没有深入展开下去;对正弦定理的证明是利用三角形的面积公式导出的,但不够自然.为了处理好这两个问题,我首先确定了一个基本原则,就是充分利用课本素材,从学生的“最近发展区”入手进行设计.具体的思路就是从解决课本的实际问题入手展开,将问题一般化导出三角形中的边角关系——正弦定理.
图1 |
某林场为了及时发现火情,在林场中设立了两个观测点A和B,某日两个观测点的林场人员分别观测到C处出现火情.在AC处观测到火情发生在北偏西40º方向,而在B处观测到火情在北偏西60º方向(如图1),已知B在A的正东方向10千米处.现在请你确定火场C距A、B多远.
要解决问题,首先应将此问题转化为数学问题
“在△ABC中,已知∠CAB=130º,∠CBA=30º,AB=10千米,求AC与BC的长.”
师:这里△ABC是斜三角形,问题是求△ABC 的边长AC与BC.一般应如何处理这类问题?
生:通常把它转化为直角三角形的问题来解决.
学生思考后,叫两个学生表述解题思路:
学生1.过A作BC的垂线,垂足为D,则
∠C=180º-130º-30º=20º,
学生2.
2.深入探究
引导学生将上述问题一般化,即“在△ABC中,已知两角(∠A,∠B)和一边(c),求其他两边(a,b)”
的问题.
师:根据上述问题的解答思路,你能否导出一个a、b的计算公式?
一个学生给出
对于BC,另一个学生给出的思路是
非常遗憾的是,当学生给出思路后,我打断学生说,这种方法太麻烦,我们看另一种思路,
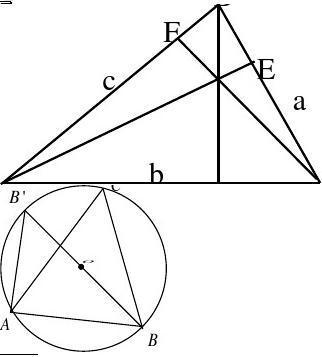
如图2,过B作CA的垂线交CA的延长线于E,则
这种思路虽然简单,但不是从学生的头脑中产生的,而是教师强加给学生的,只注意教学的结果而没有注意学生思维过程的发展,思路再好对学生的也没有指导意义.违背了以学生发展为本的原则.事实上按照学生的思路并不麻烦,可推导如下.
3.归纳、概括结论
师:由上面两个式子你能得到什么关系?
生:在△ABC中,
图3 |
也有这样的关系呢?
生1:在直角三角形ABC中,设∠C=90º,则sinC=1,
对于锐角三角形,学生A的思路是在ABC中,过A作BC边的高AD=h,
则 ,再往下没说清楚,我也没听明白学生的思路,为了赶进度,
就另叫了一个学生说出了如下的思路,直接得到结论:在锐角三角形中,
直接有 , ,可得 .
课下我问了学生A,他的推导方法是: ,又错过了一次展示学生思维过程的机会.
这样对于钝角三角形、直角三角形和锐角三角形上述关系都成立,
一般地我们得到结论:在任意△ABC中,有
我让学生用语言叙述这一关系.
本来我按课本上设计的表述是:在三角形中,各边与它所对角的正弦的比相等.而被提问的学生的表述为:在三角形中,各边与它所对角的正弦成正比.我顺势按照学生的表述,概括出正弦定理,并进一步追问:既然各边与它所对角的正弦成正比,那么这个比值是多少呢?
图4 |
师:设a是常数,我们让点A运动,保持∠A不变,那么点
A的运动轨迹如何呢?
生:在圆弧上(如图4用《几何画板》演示).
师:在运动过程中能否找到一个直角三角形,使得
∠A是直角三角形的一个锐角?
生:当BA过圆心O时,角C为直角(如图4),
比值 等于△ABC外接圆的直径,即 .
以下过程略.
教学反思
1.本节课虽然在教师的引导下,完成了教学任务,但是一味地为了完成任务而忽略了对学生正确思维的展开和引导.上好一堂课不仅有好的教学设计,还应有灵活应变的能力,只有从思想上真正转变为以学生的发展为根本,才不会为了进度而将学生强拉进自己事先设计好的轨道.正是教学有法,又无定法.
2.问题是思维的起点,是学生主动探索的动力.本节课通过对课本引例的解决、展开,引导学生在问题解决中发现结论.符合认识问题的思维规律,对激发学生探究问题兴趣是非常有益的.
3.正弦定理的证明方法很多,如利用三角形的面积公式、利用三角形的外接圆、利用向量证明等,本节课将斜三角形的边角关系转化为直角三角形的边角关系导出正弦定理,从学生的“最近发展区”入手去设计问题,思路自然,是学生们易于接受的一种证明方法.但在具体的推导时,要注意尊重学生思维的发展的过程,这是一种理念,也是一种能力.
4.在教学中恰当地利用多媒体技术,是突破教学难点的一个重要手段.本节课利用《几何画板》探究比值的值,由动到静,取得了很好的效果.而课下学生问,∠A是钝角的情形怎么证明呢?于是我将这一问题给学生留作思考题,即“你能否将∠A是钝角的情形转化为锐角的情形呢?”
在教学设计和课堂教学中应充分了解学生、研究学生,备课不仅是备知识,更重要的是备学生.作为教师只有真正树立以学生的发展为本的教学理念,才能尊重学生思维过程的发生、发展,才能从学生的生活经验和已有知识背景出发,创设合理的教学情境,才能为学生提供充分的数学活动和交流的机会,使学生从单纯的知识接受者转变为数学学习的主人.
 爱华网
爱华网