通过变动二叉树模型的步长数,可以测试二叉树模型的精度和收敛方式,由于Black-Scholes定价模型可以给出欧式期权的精确解,故这里以Black-Scholes模型给出的欧式看涨期权为对比标准价格,步长设置为1到100步,如下图
通过上图可以看到二叉树模型对于实值期权和虚值期权的收敛方式并不与平值一样具备明显趋势性,但整体上当步数足够大时,都是以震荡的方式收敛于对比标准价格。==============================================================================三叉树模型TrinomialTree Model通过变动步长数,可以测试三叉树模型的精度和收敛方式,由于Black-Scholes定价模型可以给出欧式期权的精确解,故这里以Black-Scholes模型给出的欧式看涨期权为对比标准价格,并对比三叉树模型(TrinomialTree Model)和二叉树模型(CRR Model)的精度和收敛速度,如下图:
通过上图可以看出三叉树模型(Trinomial Tree Model)的收敛速度和精度明显优于二叉树模型(CRRModel),但对于实值和虚值期权,三叉树模型(Trinomial TreeModel)在收敛过程中也有锯齿震荡现象,比二叉树模型(CRR Model)轻微一些,平滑一些。==============================================================================蒙特卡罗模拟法 Monte Carlo Method对于欧式期权,分别变动仿真次数和时间步数,使用蒙特卡罗模拟法对期权定价,对比Black-Scholes模型定价结果。
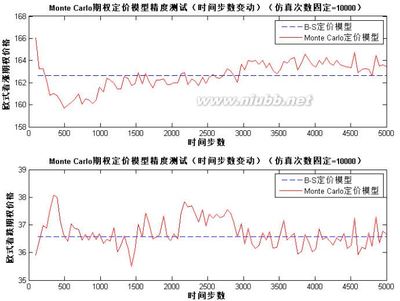
测试结果图如下:
===================================================================================================最小二乘蒙特卡罗美式期权定价模型 Least-Squares MonteCarlo Method
对于美式期权,分别变动仿真次数和时间步数,使用LSM(Least-SquaresMonteCarlo最小二乘蒙特卡罗)模型对期权定价,对比CRR模型(二叉树模型)定价结果。
测试结果图如下:
==================================================================各种定价模型都是各有利弊,适用于不同的定价标的和定价条件。
 爱华网
爱华网



