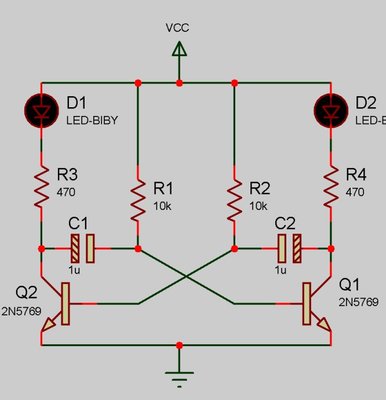
(sinusoidal current circuit)
本章主要介绍:
① 正弦量的三要素及正弦量的相量表示方法;
② 正弦电流电路中的单一元件(电阻、电感、电容);
③ RLC串、并联电路的电压和电流关系及功率;
④ 一般正弦电流电路的计算
3.1正弦量(sinusoidal function)
正弦量:大小和方向随时间按正弦规律变化的电流、电压,简称交流(AC)。
一.正弦量的三要素(three-element sinusoidal function)
正弦电压的数学表达式为
波形如图所示,其三要素:振幅 、角频率 和初相位 。
1.振幅(最大值):正弦量的变化幅度。反映正弦量变化大小的参数。
2.频率(或角频率,或周期)-----反映正弦交流电变化快慢的参数。
频率( ):正弦量在单位时间内变化的循环数,SI单位:赫兹( )。
常用千赫(KHZ)、兆赫(MHZ)等。其换算关系为
周期( ):正弦量每变化一个循环所需要的时间,SI单位:秒(s)。
角频率( ):单位时间内正弦量变化的弧度数,SI单位:弧度/秒(rad/s)。
、ω、T之间的关系:
我国工业电力网的供电频率为 , , 。
3.初相位:正弦交流电初始状态的参数。
相位角: 称为正弦量的相位角,简称相位。
初相位(初相角): 时的相位角,简称:初相。
规定:
二.相位差(phase difference)
1.相位差:两个同频率正弦量的相位之差,即为初相位之差。
例如
相位差为
①超前: , 超前 角 。
②滞后: , 滞后 角 。
③同相: ( ), 和 同相;即 和 同时达到最大。
④反相: ( 为奇数), 和 反相。
⑤正交: ( 为奇数), 和 正交。
结论:两个同频率正弦量的计时起点变化时,它们各自的初相位会跟着变化,但它们的相位差不变。
三.有效值(virtual value)
1.有效值定义:把一交变电流 和一直流电流 分别通过两个阻值相同的电阻R,如果在一个周期内,它们产生的热量相等,便称此 为 的有效值。
表示式为
2.正弦量有效值与最大值关系
即 或
注:在实际应用中,通常用有效值来表示交流电的大小。例如,电表测出的交流电压;电气设备的额定值;家庭用电的交流电压220V等等。
3.2正弦量的相量表示法
(phasor representation of sinusoidal function)
一.复数(complex function)
1.复数的表达方式及其转换
复数常用的表达方式有:公式法和图形法。
①公式法:代数式、三角函数式、指数式、极坐标形式等。
ⅰ.代数式为 、 为实数 实部,
虚部,
ⅱ.三角函数式为 为 的模, 为 的辐角。
转换关系为
(欧拉公式 )
ⅲ.指数形式
ⅳ.极坐标形式
②图形法
2.复数的运算
复数的运算符合代数运算中的交换律、结合律和分配律。
①复数的加、减运算
已知: ,
则:
②复数的乘、除运算
已知: ,
则:
③共轭复数:实部相同,虚部的数值相同而符号相反的两个复数,记作 。
二.用相量表示正弦量(phasor representation of sinusoidal function)
复指数函数 , ,则
显然有
所以正弦量可以用上述形式的复指数函数描述,使正弦量与其虚部一一对应起来。
设正弦电流
而一个复指数函数
即
正弦电流的振幅相量,记为
正弦电流的有效值相量为
相量图:相量在复平面上的几何图形。
三.同频率正弦量的和与差
(sum and difference of same frequency sinusoidal function)
同频率正弦量相加、相减、微分、积分、或与常数相乘,其频率不变,结果仍然是一个同频率的正弦量。因而同频率正弦量的加、减、微分、积分等运算,可化为它们的相量形式进行。
3.3正弦电流电路中的电阻(resistor in sinusoidal current circuit)
在正弦电流电路中,仍然适用欧姆定律和基尔霍夫定律。
一.电压和电流关系(relation between voltage and current)
如图关联参考方向下,设 ,则电流为
结论:①电压和电流为同频率的正弦量;
②电阻上的电压和电流同相位;
③有效值关系:
④相量关系: 。其中: ,
⑤欧姆定律的相量形式:
二.功率(power)
1.瞬时功率
设 ,则瞬时功率 为
由于 ,所以 ,即电阻是一个耗能元件。
2.平均功率
平均功率:瞬时功率在一个周期内的平均值(又称为有功功率),用 表示。即
它代表了电路实际消耗的功率大小,其SI单位:瓦特(W)。
例 将220V的交流电压加在额定值为220V、25W的白炽灯上,求白炽灯的电阻大小和流过白炽灯的电流。
解:
出流过白炽灯的电流
3.4正弦电流电路中的电感(inductor in sinusoidal current circuit)
一.电压和电流关系(relation between voltage and current)
如图关联参考方向下,设电感线圈中电流
则电感两端的感应电压 为
结论:①电压和电流为同频率的正弦量;
②电感上的电压超前电流 ;
③有效值关系: = , 感抗( );
④相量关系: 。其中: , ;
⑤感抗随频率变化:频率越低,感抗 就越小;直流时,电感相当于短路。感抗具有阻碍电流通过的性质。
二.功率(power)
1.瞬时功率
设 ,则瞬时功率为
结论:①在第一、三的1/4周期( 和 同相),电感吸收电源的电能( ),并转换成磁场能量储存在电感线圈中;
②第二、四的1/4周期( 和 反相),电感将储存在电感线圈中的磁场能量释放出来( ),还给电源。
③电感在电路中起能量交换作用。电感是一个储能元件,它不消耗能量。
2.平均功率
3.无功功率:反映电感在电路中与电源进行的能量交换的大小,即瞬时功率的最大值 。用 代表。单位:乏(Var)或千乏(kVar)。
3.5正弦电流电路中的电容(capacitor in sinusoidal current circuit)
一.电压和电流关系(relation between voltage and current)
如图关联参考方向下,设电容端电压为
则电容中的电流为
结论:①在纯电容电路中,电压和电流为同频率的正弦量;
②电容中的电流超前端电压 ;
③有效值关系: = , 容抗( );
④相量关系: 。其中: , ;
⑤容抗随频率变化:频率越低,容抗 就越大;直流时,电容相当于开路。容抗具有“通交流、隔直流”的作用。
二.功率(power)
1.瞬时功率
设 ,则瞬时功率为
结论:①在第一、三的1/4周期( 和 同相),电容吸收电源的电能( ),并转换成电场能量储存在电容器中;
②第二、四的1/4周期( 和 反相),电容将储存在电容器中的电场能量释放出来( ),还给电源。
③电容在电路中起能量交换作用。电容是一个储能元件,它不消耗能量。
2.平均功率
3.无功功率:反映电容元件在电路中进行能量交换的大小,用瞬时功率的最大值 ,即无功功率 表示;其单位:乏(Var)或千乏(kVar)。
3.6 串联电路( series connection circuit)
一.电压和电流关系(relation between voltage and current)
图(a)为 串联电路,选取电流、电压为关联参考方向,并设电流为
则端口电压的解析式为
(a) (b) (c)
用相量表示,如图(b)所示,得
即 -------欧姆定律的相量形式
其中 ------电压有效值关系
-------------总电压与电流的相位差电电压三角形: 、 、 组成一个直角三角形。
二.复阻抗(complex-number impedance)
RLC串联电路中
或
其中, 称为电路的复阻抗,单位:欧( );
称为电抗,单位:欧( );
为复阻抗 的模,也称为阻抗;
为复阻抗 的辐角,也称为阻抗角。
在RLC串联电路中,由于电流处处相等,将电压三角形的每边除以 ,得出新的三边( ),构成阻抗三角形。阻抗三角形与电压三角形相似。
电源电压与电流的相位差即为阻抗角,可根据电压三角形或阻抗三角形求出,即
例 一个内阻R=12Ω、电感L=160mH的线圈,与C=125μf的电容串联后,接到电压 的电源上,求电路中的电流瞬时值表达式。
解:线圈与电容串联后有
电流的瞬时值为
三.电路的三种情况(three kind state of circuit)
1. ,即 ,电路呈感性;
2. ,即 ,电路呈容性;
3. ,即 ,电源电压与电流同相,,电路呈电阻性。这种情况又称为谐振。
(a) 呈容性特性 (b) 呈阻性特性
例 日光灯电路如图所示,已知灯管电阻 为480欧姆,镇流器的电阻 为30欧姆,电感为1.5亨,当电路加上220V、50Hz的交流电压后,求电路中的电流、灯管两端的电压 、以及镇流器两端的电压 。
解:电路的等效阻抗为
电路中的电流
灯管两端的电压
镇流器两端的电压
3.7 并联电路( parallel connection circuit)
一.电压和电流关系(relation between voltage and current)
并联电路如图(a)所示,并设电压为
相量表示为
电路中电流
即 --------欧姆定律的相量形式。
由相量图可得
(a) (b) (c)
二.复导纳(complex-number admittance)
RLC并联电路中
或
其中, 称为电路的复导纳,单位:西门子(S);
( )称为电路的电导,单位:西门子(S);
称为电纳,单位:西门子(S),为容纳 ( )与感纳 ( )之差;
为复导纳 的模,也称为导纳;
为复导纳 的辐角,也称为导纳角。反映的是电路总电流超前电压的角度,即
例 在RLC并联电路中,已知R=20Ω,L=50mH,C=40μF,当该电路接入220V、50Hz的交流
电路时,求电路的复导纳为多少?写出电路中总电流瞬时值表达式。
解:电路中的复导纳
=
设电压的初相位为00,得
电流的瞬时值表达式为
三.电路的三种情况(three kind state of circuit)
1. ,即 ,总电流滞后电压,电路呈感性;
2. ,即 ,总电流超前电压,电路呈容性;
3. ,即 ,总电流 最小,电路呈电阻性。这种情况又称为RLC并联电路的谐振。
(a) 呈感性特性 (b) 呈容性特性 (c)呈阻性特性
3.8复阻抗、复导纳及其等效变换
(impedance、admittance and equivalent switch)
一.复阻抗的串、并联(series connection and parallel connection of impedance)
1.复阻抗的串联
①等效复阻抗:
②分压公式:
复阻抗的串联电路 复阻抗的并联电路
2.复阻抗的并联
①等效复导纳:
②分流公式:
③两个阻抗并联时,分流公式
二.复阻抗与复导纳的等效变换
(equivalent switch between impedance and admittance)
复阻抗 复导纳
对同一电路来说,复阻抗与复导纳互为倒数,即
或
1.已知电路的复阻抗,求等效的复导纳
已知:
则等效的复导纳为
或
即 或 不变
2.已知电路的复导纳,求等效的复阻抗
已知
则等效的复阻抗为
或
即 或 不变时
3.9几种实际电气器件的电路模型
(circuit model of electric elements)
实际的电气器件根据其特点,可以用一些理想的电路元件的组合来等效。
一.电阻器(resistor)
线绕电阻
固定
合成电阻(电阻值较大)
1.电阻(器)分类 线绕电阻
可变 (如电位器)
合成电阻
2.导体电阻的定义:
3.趋肤效应:当频率较高时,交流电流在导体截面的分布不再均匀,而是越靠近导线中间,电流密度越小;越靠近导线表面,电流密度越大。
因此,在高频电路中,为减小趋肤效应对导线电阻的影响,导线常做成管状、或将多股互相绝缘的导线紧密地绞合在一起使用。
(a)线绕电阻 (b)合成电阻 (c)可变电阻 (d)电位器
(a)合成可变电阻 (b)滑动电位器
* 当直流电流或低频电流通过线绕电阻器件时,电流在导体截面上的分布是均匀的。
二.电感器(inductor)
1.电感(器)分类
固定 铁的、钢的
①分类 ②芯子分类
可变 塑料、空气
螺线缠绕电感
③形状 环形电感
基片电感
(a)螺线缠绕电感 (b)环形电感 (c)基片电感 (d)固定电感 (e)可变电感
2.电感的等效电路
由导线绕制而成的电感器,它除了含有一定的电感L外,还含有导线的损耗(称为线圈的损耗电阻R),同时在线圈的匝间还存在电容效应(称为线圈的分布电容C),因而,在不同频率的正弦激励作用下,电路模型是不同的。
(a) (b) (c) (d) (e) (f)
图(a):一般情况。
图(b):直流。ω=0, , 。
图(c):较低频率。
图(d):频率较高(中频)。
图(e):频率相当高。线匝之间的电容不能忽略
图(f):频率足够高。感抗远远大于容抗,可认为电感处于开路状态。
三.电容器(capacitor)
1.电容(器)分类
涤纶电容器(重量轻、容量稳定)
固定
①分类 电解电容器(容量最大)
调谐电容器(微调电容)
可变
玻璃柱电容器
空气、陶瓷、涤纶
②介质材料分类
纸、云母、聚苯乙烯
(a)涤纶电容器 (b)陶瓷电容器 (c)电解电容器 (d)调谐电容器 (e)薄膜调谐电容器
2.电容器的用途:隔直流、通交流、移相、存储能量、启动电机和抑制噪声等。
3.电容器的等效电路
当正弦电压作用于电容器时,由于绝缘介质有能量损耗(包括极化损耗和漏电损耗),因而,实际的电容器与理想电容元件不同,一般等效为一个理想的电容元件与漏电阻的并联。
通常,电容器的漏电阻很大,电容器等效为一个理想电容即纯电容。
3.10正弦电流电路中的功率(power of sinusoidal current circuit)
一.瞬时功率(instantaneous power)
设无源二端网络端口电压、电流分别为
则无源二端网络的瞬时功率为
计及 ,且设 ,上式为
交流电路的瞬时功率 功率三角形
分析:① ,二端网络从外电路吸收功率,当 、 瞬时值同号时;
② ,二端网络向外电路提供功率,当 、 瞬时值异号时;
③瞬时功率有正有负的现象说明在外电路和二端网络之间有能量的往返交换。
④在一个循环内, 的部分大于 的部分,即平均来看,二端网络是从外电路吸收功率的,这是由于二端网络中存在着消耗能量的电阻。
二.有功功率、无功功率和视在功率
(active power、reactive power and apparent power)
1.有功功率:有功功率即为平均功率。
或
:功率因数
结论:①有功功率即为瞬时功率的恒定值部分,它与电压、电流有效值及它们间的相位差的余弦成正比。
②正弦电流电路中,总的有功功率等于电路各部分有功功率之和。
2.无功功率
定义正弦电流电路的无功功率Q为
正弦电流电路中,总的无功功率等于电路各部分无功功率之和;即
3.视在功率
视在功率是用来表示电气设备的容量大小的,用S表示。其定义为
单位:伏安( )。
有功功率、无功功率和视在功率的关系
、 、 、
*有功功率、无功功率和视在功率构成一个直角三角形,称为功率三角形。
三.复功率(complex power)
复功率 定义:
可知: ,
* 注意:①复功率与阻抗相似,它是一个复数量。并不代表正弦量,因此不能作为相量对待。
②对正弦电路,因有功功率和无功功率是守恒的,所以复功率也守恒,即在整个电路中某些支路吸收的复功率应该等于其余支路发出的复功率。
例 某一电路由三个复阻抗串联构成,其中 , , ,电源电压 ,求
(1)电路中的电流;
(2)各阻抗上的电压;
(3)电路的有功功率、无功功率、视在功率及电路的功率因数。
解:(1)电路总的复阻抗为
电路中的电流为
(2)各阻抗上的电压为
(3)
、 、 、
四.功率因数及功率因数的改善(power factor and power-factor improved)
1.功率因数的定义
,
2.改善功率因数原因
① 低 电源设备的容量不能充分利用。( 一定, 小)。
② 低 在供电线路上能量损耗和电压降低较大,引起负载电压的降低,影响负载的正常工作。( 一定, 大)。
可见:提高用电的功率因数,能使电源设备的容量得到合理的利用,减少输电电能损耗,又能改善供电的电压质量。
3.改善功率因数方法及原理:在感性负载两端并上一个合适的补偿电容。
例 一台电动机的功率为1.2kW,接到220V的工频电源上,其工作电流为10A,试求:(1)电动机的功率因数;
(2)若在电动机两端并上一只80μF的电容器,此时电路的功率因数为多少?
解:(1)根据题意,电动机的有功功率及电路的视在功率为
电动机的功率因数为
(2)电动机两端并上电容器后,如图(a)所示,相量图如图(b)所示。
(a) (b)
根据相量图得
所以
电路的功率因数变为
3.11一般正弦电流电路的计算
(analysis of the sinusoidal current circuit)
一.最大功率传输(transmission of most power)
电路中的一个重要内容是:如何将信号功率最大限度传递给下一级电路——最大功率的传输。
根据戴维南定理,任何有源二端网络都可以用一个有源支路来替代。因而,电路的功率传输问题,转化为电源输出功率的问题。
(a) (b)
1.负载获得最大功率的条件及最大功率
如图所示,若 ,其复阻抗 ,负载 ,则负载吸收的有功功率为
令 , ,可求出负载获得的最大功率。
条件: , 或
最大功率为:
例 如图电路中,已知 , ,问负载为何值时,可获得最大功率。若 变为 ,则负载上的最大功率有何变化?
解:当 时,负载可获得最大功率。最大功率为
当 变为 时,负载为 ,获得最大功率为
即 不变
二.正弦电流电路的一般分析方法与计算
前面介绍的节点电压法、网孔电流法、叠加定理以及戴维南定理等电路的分析方法,均可用于正弦电流电路,不同的是,正弦电流电路中的电压和电流用相量来表示,电路元件用复阻抗来表示。
例 用节点电压法求图示电路中电流 的瞬时值表达式。已知
, , 。
解:各支路的复导纳分别为
电压 、 的相量形式为
选择b为参考结节点,则a点的节点电压为
所以
例 在图示电路中,已知 , , , , , ,用网孔电流法求电流 的瞬时值表达式。
解:设网孔电流为 、 、 ,其绕行方向如图所示
网孔电压方程分别为
即
联立求解方程得
例 两台相同的交流发电机并联运行,同时为负载 供电,如图所示。已知发电机的电源电压 ,内阻为 ,负载 ,用戴维南定理求出负载上的电压 与电流 ,以及负载消耗的功率大小。
(a) 流发电机供电电路 (b)戴维南等效电路
解:根据戴维南定理,求开路电压和等效阻抗
所以
负载中电流
负载端电压
负载消耗的功率
 爱华网
爱华网