分类: 数据结构 2012-08-12 20:42 265人阅读 评论(0) 收藏 举报
nullinsertdeletetreeclass算法
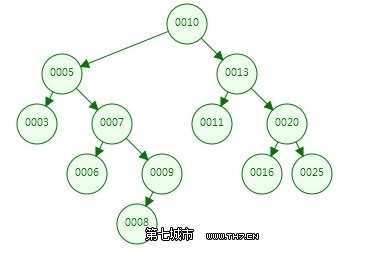
二叉排序树(Binary Sort Tree)又称二叉查找树。 它是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
二叉排序树是一种动态树表。
vs2008运行正确,如有误,请各位大牛指正!
实现代码如下:
[cpp] view plaincopyprint?
//MyBiSortTree.cpp:定义控制台应用程序的入口点。
//二叉查找树的各种操作
//实现功能:建树,查找,插入,删除,求最大值最小值,求双亲结点
//,获取中序遍历的前驱结点后继结点,用栈实现非递归的先序中序后序遍历算法,
#include"stdafx.h"
#include<iostream>
usingnamespacestd;
inta[100];//存放结点数据的数组
constintSTACK_MAXSIZE=30;
//二叉排序树的结点类型
classBSNode
{
public:
BSNode(){};
BSNode(intitem):data(item),m_lchild(NULL),m_rchild(NULL){}
intdata;//数据域
BSNode*m_lchild;//左孩子
BSNode*m_rchild;//右孩子
};
//二叉排序树类型
classBSTree
{
public://定义接口
BSTree();
//建树:创建一棵结点个数为n的二叉排序树
voidCreateTree();
//查找:在以root为根的树上查找值为item的结点,返回给Node,找到返回true,否则为false
boolFindNode(intitem);
//插入:在以root为根的树上插入值为item的结点
voidInsertNode(intitem);
//删除:在以root为根的树上插入值为item的结点
voidDeleteNode(intitem);
//求最大值:返回以root为根的树中结点的最小值,结点返回给minNode
intMinNode();
//求最小值:返回以root为根的树中结点的最大值,结点返回给maxNode
intMaxNode();
//求双亲结点:返回值为item的结点的双亲结点
BSNode*GetParent(intitem);
//获取中序遍历的前驱结点
BSNode*GetInOrderPre(intitem);
//获取中序遍历的后继结点
BSNode*GetInOrderPost(intitem);
//用栈实现非递归的先序遍历
voidPreOrderVisit();
//用栈实现非递归的中序遍历
voidInOrderVisit();
//用栈实现非递归的后序遍历
voidPostOrderVisit();
private:
BSNode*root;//树的根结点
//建树:创建一棵结点个数为n的二叉排序树
voidCreate(BSNode*&root,int*a,intn);
//查找:在以root为根的树上查找值为item的结点,返回给Node,找到返回true,否则为false
boolFind(BSNode*&root,BSNode*&Node,intitem);
//插入:在以root为根的树上插入值为item的结点
voidInsert(BSNode*&root,intitem);
//删除:在以root为根的树上插入值为item的结点
voidDelete(BSNode*&root,intitem);
//求最大值:返回以root为根的树中结点的最小值,结点返回给minNode
intMin(BSNode*root,BSNode*&minNode);
//求最小值:返回以root为根的树中结点的最大值,结点返回给maxNode
intMax(BSNode*root,BSNode*&maxNode);
//求双亲结点:返回值为item的结点的双亲结点
BSNode*getParent(BSNode*root,intitem);
//获取中序遍历的前驱结点
BSNode*getInOrderPre(BSNode*root,intitem);
//获取中序遍历的后继结点
BSNode*getInOrderPost(BSNode*root,intitem);
//用栈实现非递归的先序遍历
voidPreOrder(BSNode*root);
//用栈实现非递归的中序遍历
voidInOrder(BSNode*root);
//用栈实现非递归的后序遍历
voidPostOrder(BSNode*root);
};
BSTree::BSTree()
{
root=NULL;
}
//建树:创建一棵结点个数为n的二叉排序树
voidBSTree::CreateTree()
{
intn=0;
Create(root,a,n);
}
//建树:创建一棵结点个数为n的二叉排序树
voidBSTree::Create(BSNode*&root,int*a,intn)//待续,要利用插入算法
{
cout<<"请输入树的结点个数:";
cin>>n;
cout<<endl<<"请依次输入结点的数值:"<<endl;
BSNode*newNode=NULL;
for(inti=0;i<n;i++)
{
cin>>a[i];
InsertNode(a[i]);
}
}
//查找:在以root为根的树上查找值为item的结点,返回给Node,找到返回true,否则为false
boolBSTree::FindNode(intitem)
{
BSNode*Node=NULL;
returnFind(root,Node,item);
}
//查找:在以root为根的树上查找值为item的结点,返回给Node,找到返回true,否则为false
boolBSTree::Find(BSNode*&root,BSNode*&findNode,intitem)
{
if(root==NULL)//树空
{
findNode=NULL;//没有找到结点
returnfalse;
}
else
{
if(root->data==item)
{
findNode=root;//找到结点
returntrue;
}
elseif(root->data>item)//数值小于根结点的数值,则在左子树中递归查找
{
returnFind(root->m_lchild,findNode,item);
}
else//数值大于根结点的数值,则在右子树中递归查找
{
returnFind(root->m_rchild,findNode,item);
}
}
}
//插入:在以root为根的树上插入值为item的结点
voidBSTree::InsertNode(intitem)
{
Insert(root,item);
}
//插入:在以root为根的树上插入值为item的结点
//根为空,则直接插入;根不空,则在插入之前先要查找该数值的结点是否存在
voidBSTree::Insert(BSNode*&root,intitem)
{
BSNode*newNode=NULL;
if(root==NULL)//树为空,则先建立根结点
{
newNode=newBSNode(item);
root=newNode;
cout<<item<<"已被插入二叉排序树中!"<<endl;
}
else
{
if(FindNode(item))//如果找到该数值的结点,直接返回
{
cout<<"数值"<<item<<"已经存在!"<<endl;
return;
}
if(item>root->data)//当前数值比根结点大,则插入树的右子树
{
Insert(root->m_rchild,item);
}
else
{
Insert(root->m_lchild,item);
}
}
}
//删除:在以root为根的树上删除值为item的结点
voidBSTree::DeleteNode(intitem)
{
Delete(root,item);
}
//删除:在以root为根的树上删除值为item的结点
voidBSTree::Delete(BSNode*&root,intitem)
{
BSNode*pNode=NULL;
if(root==NULL)
{
cout<<"树空!"<<endl;
return;
}
if(Find(root,pNode,item))
{
BSNode*pParent=NULL;
//情况一:叶子结点
if(pNode->m_lchild==NULL&&pNode->m_rchild==NULL)//被删除结点是叶子结点
{
if(pNode==root)//且是根结点
{
root=NULL;
}
else//且不是根结点
{
pParent=GetParent(item);
if(pParent->m_lchild==pNode)//为其父亲结点的左孩子
{
pParent->m_lchild=NULL;
}
else//为其父亲结点的右孩子
{
pParent->m_rchild=NULL;
}
}
}
//情况二:只有一个孩子结点
elseif(pNode->m_rchild!=NULL&&pNode->m_lchild==NULL)//被删除结点有右孩子,无左孩子
{
if(pNode==root)//且是根结点
{
root=pNode->m_rchild;
}
else//且不是根结点
{
pParent=GetParent(item);//找到给结点的父亲节点
if(pParent->m_lchild==pNode)
{
pParent->m_lchild=pNode->m_rchild;
}
else
{
pParent->m_rchild=pNode->m_rchild;
}
}
}
elseif(pNode->m_lchild!=NULL&&pNode->m_rchild==NULL)//被删结点有左孩子,无右孩子
{
if(pNode==root)//且是根结点
{
root=pNode->m_lchild;
}
else//且不是根结点
{
pParent=GetParent(item);//找到给结点的父亲节点
if(pParent->m_lchild==pNode)
{
pParent->m_lchild=pNode->m_lchild;
}
else
{
pParent->m_rchild=pNode->m_lchild;
}
}
}
//情况三:有两个孩子结点
elseif(pNode->m_lchild!=NULL&&pNode->m_rchild!=NULL)//被删结点有左孩子和右孩子
{
//解法一:找到该结点的前驱结点(右孩子必为空)
BSNode*maxNode=NULL;
intmax=Max(pNode->m_lchild,maxNode);//找到以该结点左孩子为根的子树上最大的结点,即为其前驱结点
BSNode*father=GetParent(max);
pNode->data=max;//将前驱结点的值赋给该结点
if(father!=pNode)
{
father->m_rchild=maxNode->m_lchild;
}
else
{
father->m_lchild=maxNode->m_lchild;
}
//解法二:找到该结点的后继结点(左子树必为空)
//BSNode*minNode=NULL;
//intmin=Min(pNode->m_rchild,minNode);//找到以该结点右孩子为根的子树上最小的结点,即为其后继结点
//BSNode*father=GetParent(min);
//pNode->data=min;//将后继结点的值赋给该结点
//if(father!=pNode)
//{
//father->m_lchild=minNode->m_rchild;
//}
//else
//{
//father->m_rchild=minNode->m_rchild;
//}
//解法三:让该结点的左子树为其父亲结点的左子树(或右子树,取决于该结点是父亲结点的左子树还是右子树),
//其右子树为其前驱结点(以该结点左孩子为根的子树中最大值结点)的右子树
//BSNode*Father=GetParent(item);
//if(Father==NULL)//该结点是根结点
//{
//root=pNode->m_lchild;
//BSNode*maxNode=NULL;
//intmax=Max(pNode->m_lchild,maxNode);
//maxNode->m_rchild=pNode->m_rchild;
//}
//else//该结点不是根结点
//{
//if(Father->m_lchild==pNode)
//{
//Father->m_lchild=pNode->m_lchild;
//}
//else
//{
//Father->m_rchild=pNode->m_lchild;
//}
////BSNode*maxNode=GetInOrderPre(item);
//BSNode*maxNode=NULL;
//intmax=Max(pNode->m_lchild,maxNode);
//maxNode->m_rchild=pNode->m_rchild;
//}
}
if(root==NULL)
{
cout<<"删除结点后,二叉排序树为空!"<<endl;
}
else
{
cout<<"结点"<<item<<"删除成功!"<<endl;
}
}
else
{
cout<<"数值为"<<item<<"的结点不存在!"<<endl;
}
}
//求最小值:返回以root为根的树中结点的最小值,结点返回给minNode
intBSTree::MinNode()
{
BSNode*minNode;
returnMin(root,minNode);
}
//求最小值:返回以root为根的树中结点的最小值,结点返回给minNode
intBSTree::Min(BSNode*root,BSNode*&minNode)
{
intmin=0;
BSNode*p=root;
if(p==NULL)
{
cout<<"树空!"<<endl;
return-1;//结果为-1表示树空,最小值不存在
}
else
{
while(p->m_lchild)
{
p=p->m_lchild;
}
minNode=p;
returnminNode->data;
}
returnmin;
}
//求最大值:返回以root为根的树中结点的最大值,结点返回给maxNode
intBSTree::MaxNode()
{
BSNode*maxNode=NULL;
returnMax(root,maxNode);
}
//求最大值:返回以root为根的树中结点的最大值,结点返回给maxNode
intBSTree::Max(BSNode*root,BSNode*&maxNode)
{
intmax=0;
BSNode*p=root;
if(p==NULL)
{
cout<<"树空!"<<endl;
return-1;//结果为-1表示树空,最大值不存在
}
else
{
while(p->m_rchild)
{
p=p->m_rchild;
}
maxNode=p;
returnmaxNode->data;
}
returnmax;
}
//求双亲结点:返回值为item的结点的双亲结点
BSNode*BSTree::GetParent(intitem)
{
returngetParent(root,item);
}
//求双亲结点:返回值为item的结点的双亲结点
BSNode*BSTree::getParent(BSNode*root,intitem)
{
BSNode*pParent=NULL;//指向双亲结点的指针
BSNode*pNode=NULL;
if(Find(root,pNode,item))//找到值为item的结点
{
if((root==NULL)||(root==pNode))//树空,或该结点为根结点,则不存在双亲结点
{
pParent=NULL;
}
else//树不空且该结点不是根结点
{
if(root->m_lchild==pNode||root->m_rchild==pNode)
{
pParent=root;
}
elseif(root->data>item)
{
pParent=getParent(root->m_lchild,item);
}
else
{
pParent=getParent(root->m_rchild,item);
}
}
returnpParent;
}
else
{
cout<<"不存在值为"<<item<<"的结点!";
returnpParent;
}
}
//获取中序遍历的前驱结点
BSNode*BSTree::GetInOrderPre(intitem)
{
returngetInOrderPre(root,item);
}
//获取中序遍历的前驱结点
//思想:先找到对应的结点,如果该结点的左孩子不空,找到以它的左孩子为根的子树中的最大值结点
//否则如果该结点的左孩子空,找到第一个有右孩子的祖先结点
BSNode*BSTree::getInOrderPre(BSNode*root,intitem)
{
BSNode*pPre=NULL;//指向该结点的前驱结点的指针
BSNode*pNode=NULL;
if(Find(root,pNode,item))//找到对应的结点
{
if(pNode->m_lchild!=NULL)//该结点的左孩子不空
{
BSNode*maxNode=NULL;
intmax=Max(pNode->m_lchild,maxNode);//找到以它的左孩子为根的子树中的最大值结点
pPre=maxNode;
}
else//该结点的左孩子为空
{
//找到第一个有右孩子的祖先结点
BSNode*pParent=GetParent(item);
;
while(pParent->m_rchild==NULL)//右孩子为空
{
pParent=GetParent(pParent->data);
}
pPre=pParent;
}
returnpPre;
}
else
{
cout<<"数值为"<<item<<"的结点不存在!";
returnpNode;
}
}
//获取中序遍历的后继结点
//思想:先找到对应的结点,如果右孩子节点非空,则找到右子树的最小值节点
//否则如果右孩子节点为空,则找到第一个有左孩子节点的其祖辈节点
BSNode*BSTree::GetInOrderPost(intitem)
{
returngetInOrderPost(root,item);
}
//获取中序遍历的后继结点
BSNode*BSTree::getInOrderPost(BSNode*root,intitem)
{
BSNode*pPost=NULL;//指向后继结点的指针
BSNode*pNode=NULL;
if(Find(root,pNode,item))
{
if(pNode->m_rchild!=NULL)//该结点的右孩子不空
{
//找到以其右孩子为根的子树中最小值的结点
BSNode*minNode=NULL;
intmint=Min(pNode->m_rchild,minNode);
pPost=minNode;
}
else//该结点的右孩子为空
{
//找到第一个有左孩子的祖先结点
BSNode*pParent=GetParent(item);
while(pParent->m_lchild==NULL)
{
pParent=GetParent(pParent->data);
}
pPost=pParent;
}
returnpPost;
}
else
{
cout<<"数值为"<<item<<"的结点不存在!"<<endl;
returnpPost;
}
}
//用栈实现非递归的先序遍历
voidBSTree::PreOrderVisit()
{
PreOrder(root);
}
//用栈实现非递归的先序遍历
voidBSTree::PreOrder(BSNode*root)
{
//定义栈
BSNode*stack[STACK_MAXSIZE];
inttop=0;//top为0表示栈空,指向栈顶的下一个位置
BSNode*p=root;
cout<<"二叉树的先序遍历:";
while(p||(top!=0))//指针不空或栈不空
{
if(p)
{
stack[top++]=p;//入栈
cout<<p->data<<"";//访问该结点
p=p->m_lchild;
}
else
{
p=stack[--top];//出栈
p=p->m_rchild;
}
}
cout<<endl;
}
//用栈实现非递归的中序遍历
voidBSTree::InOrderVisit()
{
InOrder(root);
}
//用栈实现非递归的中序遍历
voidBSTree::InOrder(BSNode*root)
{
//定义栈
BSNode*stack[STACK_MAXSIZE];
inttop=0;//top为0表示栈空,指向栈顶的下一个位置
BSNode*p=root;
cout<<"二叉树的中序遍历:";
while(p||(top!=0))//指针不空或栈不空
{
if(p)
{
stack[top++]=p;//入栈
p=p->m_lchild;
}
else
{
p=stack[--top];//出栈
cout<<p->data<<"";//访问该结点
p=p->m_rchild;
}
}
cout<<endl;
}
//用栈实现非递归的后序遍历,后序遍历较为复杂,需要用到两个栈
voidBSTree::PostOrderVisit()
{
PostOrder(root);
}
//用栈实现非递归的后序遍历,后序遍历较为复杂,需要用到两个栈
voidBSTree::PostOrder(BSNode*root)
{
//定义栈
BSNode*stack1[STACK_MAXSIZE];
BSNode*stack2[STACK_MAXSIZE];
inttop1=0;//top为0表示栈空,指向栈顶的下一个位置
inttop2=0;
BSNode*p=root;
cout<<"二叉树的后序遍历:";
while(p||(top1!=0))//指针不空或栈不空
{
if(p)
{
stack1[top1++]=p;//入栈1
stack2[top2++]=p;//入栈2
p=p->m_rchild;//注意此处是指向右孩子
}
else
{
p=stack1[--top1];//栈1的栈顶元素出栈,栈2元素不出栈
p=p->m_lchild;
}
}
while(top2!=0)
{
p=stack2[--top2];//栈2栈顶元素出栈
cout<<p->data<<"";//访问该结点
}
cout<<endl;
}
int_tmain(intargc,_TCHAR*argv[])
{
BSTreetree;
tree.CreateTree();
tree.PreOrderVisit();
tree.InOrderVisit();
tree.PostOrderVisit();
intitem=0;
cout<<"请输入要查找的结点值:";
cin>>item;
cout<<item<<"存在返回1,否则返回0.结果是:"<<tree.FindNode(item)<<endl;
cout<<item<<"的双亲是:";
if(tree.GetParent(item))
{
cout<<tree.GetParent(item)->data<<endl;
}
else
{
cout<<"该结点为根结点,不存在双亲!"<<endl;
}
cout<<item<<"中序遍历序列中前驱结点值是:"<<tree.GetInOrderPre(item)->data<<endl;
cout<<item<<"中序遍历序列中后继结点值是:"<<tree.GetInOrderPost(item)->data<<endl;
tree.InsertNode(100);
tree.InsertNode(48);
tree.DeleteNode(50);
tree.DeleteNode(45);
tree.DeleteNode(55);
tree.InOrderVisit();
cout<<"二叉排序树中,最大值为:"<<tree.MaxNode()<<endl;
cout<<"二叉排序树中,最小值为:"<<tree.MinNode()<<endl;
system("pause");
return0;
}
 爱华网
爱华网