例子:假设我们有一个信号,它含有a、2V的直流分量,b、频率为50Hz、相位为-30度、幅度为3V的交流信号,以及c、频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下:S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。 式中cos参数为弧度,所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样,采样时间为1秒,数据长度为256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT的(部分)结果的模值如下所示,我们把在第1点、第51点、和第76点附近的数据拿上来细看: 1点: 512+0i 2点: -2.6195E-14 -1.4162E-13i 3点: -2.8586E-14 -1.1898E-13i 50点:-6.2076E-13 -2.1713E-12i 51点:332.55 - 192i 52点:-1.6707E-12 -1.5241E-12i 75点:-2.2199E-13-1.0076E-12i 76点:3.4315E-12 +192i 77点:-3.0263E-14+7.5609E-13i 很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下: 1点: 512 51点:384 76点:192 按照公式,可以计算出直流分量为:512/N=512/256=2;50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见,从频谱分析出来的幅度是正确的。 然后再来计算相位信息。直流信号没有相位可言,不用管它。先计算50Hz信号的相位,atan2(-192,332.55)=-0.5236,结果是弧度,换算为角度就是180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位,atan2(192,3.4315E-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。可见,相位也是对的。根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
原文的总结:总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。要精确到xHz,则需要采样长度为1/x秒的信号,并做FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。
加一点我自己的理解:1、无论采样时间是多少,数据长度是多少,离散傅里叶变换的第一项是直流分量。只要计算不错,如何理解是你自己的事。举个例子,如果我们有一个1Hz的正弦波,你的采样时间是0.5秒,正好采了这个1Hz正弦波的正半周,那么无论你的数据长度是多少(即采样频率有多高),你的变换结果中一定有很大的直流分量。如何理解这个直流分量?可见,变换结果的判读是十分重要的,另外,对于信号的先验知识是更加重要的,因为它可以帮助我们正确地设计采样时间、采样频率,以及事后对变换结果的正确判读。 2、离散傅里叶变换的第二项是基频,也就是可以分辨的最小频率(间隔),这是由采样时间决定的,即采样时间的倒数。例如,我的采样时间是1秒,那么频率分辨率就是1Hz,如果我要分辨到0.5Hz,那么采样时间就得是2秒。3、数据长度决定倍频的次数。例如,采样长度是16个点,那么转换结果第一个值是直流分量,第二个值是基频,第三个就是2倍频,第四个是三倍频,依此类推,N个数据,可以到N-1倍频。4、幅值与相位的计算,前面说了,不多说了。5、补零可以提高频率分辨率吗?清华程佩青认为不可以。例如,实际采样了1秒时间,补了1秒的零,计算的频率分辨率显然提高了。为什么不可以?程佩青说“实际的”频率分辨率还得按实际的测量数据的长度来算,这怎么看?我认为,无论实际采样的长短如何,它是真实的,在补了零以后,你就把数据的形态给改变了,你让傅里叶变换认为实际数据中有一段是持续的零,那么你在理解变换的结果的时候也得充分考虑补零带来的影响。否则显然会理解错误。
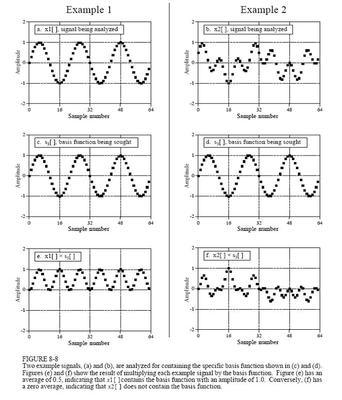
上面的“第x个数”,是按我们一般习惯的说法,因此没有“第0个数”这种说法。如果按照C语言的习惯,一个数组的下标从0开始,那么就是“第0个数”是直流分量,第一个数是基频(一倍频),下标是几就是几倍频,这样是否有助于理解呢?
原作者是用Matlab做的实验,附了源程序,如下:[附录:本测试数据使用的matlab程序]clc;clear;Adc=2; %直流分量幅度A1=3; %频率F1信号的幅度A2=1.5; %频率F2信号的幅度F1=50; %信号1频率(Hz)F2=75; %信号2频率(Hz)Fs=256; %采样频率(Hz)P1=-30; %信号1相位(度)P2=90; %信号相位(度)N=256; %采样点数t=[0:1/Fs:N/Fs]; %采样时刻%信号S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);%显示原始信号subplot(411);plot(S);title('原始信号');
Y = fft(S,N); %做FFT变换Ayy = (abs(Y)); %取模subplot(412);stem(Ayy(1:N)); %显示原始的FFT模值结果title('FFT 模值');Ayy=Ayy/(N/2); %换算成实际的幅度Ayy(1)=Ayy(1)/2;F=([1:N]-1)*Fs/N; %换算成实际的频率值,Fn=(n-1)*Fs/Nsubplot(413);stem(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果title('幅度-频率曲线图');Pyy=[1:N/2];for i=1:N/2Pyy(i)=angle(Y(i)); %计算相位Pyy(i)=Pyy(i)*180/pi; %换算为角度end;subplot(414);stem(F(1:N/2),Pyy(1:N/2)); %显示相位图title('相位-频率曲线图');
 爱华网
爱华网