拓扑排序的三种方法 拓扑排序 c

拓扑排序

通常，这样的线性序列称为满足拓扑次序(TopologicalOrder)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。离散数学中关于偏序和全序的定义：

　　若集合X上的关系是R是自反的、反对称的和传递的，则称R是集合X上的偏序关系。

　　设R是集合X上的偏序（Partial Order）,如果对每个x,y属于X必有xRy 或yRx，则称R是集合X上的全序关系。

　　注意：

　　①若将图中顶点按拓扑次序排成一行，则图中所有的有向边均是从左指向右的。

　　②若图中存在有向环，则不可能使顶点满足拓扑次序。

　　③一个DAG的拓扑序列通常表示某种方案切实可行

本节说明了如何用深度优先搜索，对一个有向无回路图进行拓扑排序。有向无回路图又称为dag。对这种有向无回路图的拓扑排序的结果为该图所有顶点的一个线性序列，满足如果G包含(u,v)，则在序列中u出现在v之前（如果图是有回路的就不可能存在这样的线性序列)。一个图的拓扑排序可以看成是图的所有顶点沿水平线排成的一个序列，使得所有的有向边均从左指向右。因此，拓扑排序不同于通常意义上对于线性表的排序。

有向无回路图经常用于说明事件发生的先后次序，图1给出一个实例说明早晨穿衣的过程。必须先穿某一衣物才能再穿其他衣物(如先穿袜子后穿鞋)，也有一些衣物可以按任意次序穿戴(如袜子和短裤)。图1(a)所示的图中的有向边(u,v)表明衣服u必须先于衣服v穿戴。因此该图的拓扑排序给出了一个穿衣的顺序。每个顶点旁标的是发现时刻与完成时刻。图1(b)说明对该图进行拓扑排序后将沿水平线方向形成一个顶点序列，使得图中所有有向边均从左指向右。

下列简单算法可以对一个有向无回路图进行拓扑排序。

procedure Topological_Sort(G);begin 1.调用DFS(G)计算每个顶点的完成时间f[v]; 2.当每个顶点完成后，把它插入链表前端; 3.返回由顶点组成的链表;end;

图1(b)说明经拓扑排序的结点以与其完成时刻相反的顺序出现。因为深度优先搜索的运行时间为θ(V+E)，每一个v中结点插入链表需占用的时间为θ(1)，因此进行拓扑排序的运行时间θ(V+E)。

图1 早晨穿衣的过程

为了证明算法的正确性，我们运用了下面有关有向无回路图的重要引理。

引理1

有向图G无回路当且仅当对G进行深度优先搜索没有得到反向边。

证明：

→：假设有一条反向边(u,v)，那么在深度优先森林中结点v必为结点u的祖先，因此G中从v到u必存在一通路，这一通路和边(u,v)构成一个回路。

←：假设G中包含一回路C，我们证明对G的深度优先搜索将产生一条反向边。设v是回路C中第一个被发现的结点且边(u,v)是C中的优先边，在时刻d[v]从v到u存在一条由白色结点组成的通路，根据白色路径定理可知在深度优先森林中结点u必是结点v的后裔，因而(u,v)是一条反向边。(证毕)

定理1

Topological_Sort(G)算法可产生有向无回路图G的拓扑排序。

证明:

假设对一已知有问无回路图G=(V,E)运行过程DFS以确定其结点的完成时刻。那么只要证明对任一对不同结点u,v∈V，若G中存在一条从u到v的有向边，则f[v]<f[u]即可。考虑过程DFS(G)所探寻的任何边(u,v)，当探寻到该边时，结点v不可能为灰色，否则v将成为u的祖先，(u,v)将是一条反向边，和引理1矛盾。因此，v必定是白色或黑色结点。若v是白色，它就成为u的后裔，因此f[v]<f[u]。若v是黑色，同样f[v]<f[u]。这样一来对于图中任意边(u,v)，都有f[v]<f[u]，从而定理得证。（证毕）

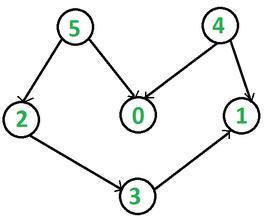
另一种拓扑排序的算法基于以下思想：首先选择一个无前驱的顶点（即入度为0的顶点，图中至少应有一个这样的顶点，否则肯定存在回路），然后从图中移去该顶点以及由他发出的所有有向边，如果图中还存在无前驱的顶点，则重复上述操作，直到操作无法进行。如果图不为空，说明图中存在回路，无法进行拓扑排序；否则移出的顶点的顺序就是对该图的一个拓扑排序。

下面是该算法的具体实现：

procedure Topological_Sort_II(G);begin  1  for 每个顶点u∈V[G] do d[u]←0;  //初始化d[u],d[u]用来记录顶点u的入度2  for 每个顶点u∈V[G] do3    for 每个顶点v∈Adj[u] do d[v]←d[v]+1;  //统计每个顶点的入度4  CreateStack(s);  //建立一个堆栈s5  for 每个顶点u∈V[G] do    6    if d[u]=0 then push(u,s);  //将度为0的顶点压入堆栈7  count←0;     8  while (not Empty(s)) do     begin9      u←top(s);  //取出栈顶元素10     pop(s);     //弹出一个栈顶元素11     count←count+1;12     R[count]←u;   //线性表R用来记录拓扑排序的结果13     for 每个顶点v∈Adj[u] do //对于每个和u相邻的节点v             begin14                 d[v]←d[v]-1;15                 if d[v]=0 then push(v,s);  //如果出现入度为0的顶点将其压入栈                 end;                         end;         16 if count<>G.size then writeln('Error! The graph has cycle.')17                  else 按次序输出R;end;

上面的算法中利用d[u]来记录顶点u的入度，第2-3行用来统计所有顶点的入度，第5-6行将入度为0的顶点压入堆栈，第8-15行不断地从栈顶取出顶点，将该顶点输出到拓扑序列中，并将所有与该顶点相邻的顶点的入度减1，如果某个顶点的入度减至0，则压入堆栈，重复该过程直到堆栈空了为止。显而易见该算法的复杂度为O(VE)，因为第2-3行的复杂性就是O(VE)，后面8-15行的复杂性也是O(VE)。这个算法虽然简单，但是没有前面一个算法的效率高。

//=========================================================================================

爱华网本文地址 » http://www.aihuau.com/a/25101011/84852.html