标签:二叉树linux分类: linux 内存
linux 内存管理之红黑树
谨以此文纪念过往的岁月。
我们可以将经常需要被读取的数据定义为 __read_mostly类型, 这样Linux内核被加载时,该数据将自动被存放到Cache中,以提高整个系统的执行效率
一.红黑树
1.1什么是红黑树
红黑树是满足一定特征的二叉树,其本质还是二叉树。
一般的,红黑树,满足以下性质,即只有满足以下全部性质的树,我们才称之为红黑树:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
其每一个红黑树的节点包括三个参数node_color,node_left,node_right。
http://blog.csdn.net/v_JULY_v/archive/2010/12/29/6105630.aspx 博文详细的讲述了红黑树的操作。
1.2linux中如何实现红黑树
1.2.1红黑树结构体
__attribute__((aligned(sizeof(long)))); --声明结构体long类型对齐。
红黑根节点描述
struct rb_root
{
struct rb_node *rb_node;
};
红黑树节点描述
struct rb_node
{
unsigned long rb_parent_color; --保存节点color同时保存父节点的指针值
#defineRB_RED0
#defineRB_BLACK1
struct rb_node *rb_right; --右子
struct rb_node *rb_left; --左子
}
设置父节点。
static inline void rb_set_parent(struct rb_node *rb, struct rb_node *p)
{
rb->rb_parent_color = (rb->rb_parent_color & 3) | (unsigned long)p;
}
设置节点颜色
static inline void rb_set_color(struct rb_node *rb, int color)
{
rb->rb_parent_color = (rb->rb_parent_color & ~1) | color;
}
1.2.2红黑树的操作
红黑树的最主要特征在于其颜色满足特定的性质。普通的节点添加,极有可能破坏红黑树的性质,所以在添加红黑树节点时,需要将整个红黑树的颜色进行调整。
下面以rb_insert_color为例。
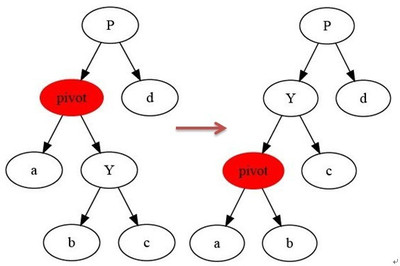
在理解下面的程序前要先理解两个函数,即红黑树的左旋和右旋。
左旋:
对照上图可以更好的理解下面的程序。将node设置为pivot,root不管。
static void __rb_rotate_left(struct rb_node *node, struct rb_root *root)
{
struct rb_node *right = node->rb_right; --right = Y
struct rb_node *parent = rb_parent(node); --parent = P
if ((node->rb_right = right->rb_left)) --pivot的右子设置为P的左子即pivot->rb_right = b
rb_set_parent(right->rb_left, node); --同时将b->parent 设置为pivot
right->rb_left = node; --将pivot设置为Y的左子
rb_set_parent(right, parent); --设置Y的parent为P
if (parent)
{
if (node == parent->rb_left) --如果pivot为P的左子
parent->rb_left = right; --则P的右子设置为Y
else
parent->rb_right = right; --否则P的左子设置为Y
}
else
root->rb_node = right;
rb_set_parent(node, right); --设pivot的parent为Y
}
对于右旋参照左旋即可了,这两个旋转类似。
static void __rb_rotate_right(struct rb_node *node, struct rb_root *root)
{
struct rb_node *left = node->rb_left;
struct rb_node *parent = rb_parent(node);
if ((node->rb_left = left->rb_right))
rb_set_parent(left->rb_right, node);
left->rb_right = node;
rb_set_parent(left, parent);
if (parent)
{
if (node == parent->rb_right)
parent->rb_right = left;
else
parent->rb_left = left;
}
else
root->rb_node = left;
rb_set_parent(node, left);
}
关于左旋和右旋都是为了保证平衡二叉树的性质不变,即是通过左旋和右旋来保证红黑二叉树的第五条性质满足。
红黑二叉树的添加跟普通的二叉树的添加类似。不过在添加节点后需要对节点的颜色进行调整,甚至对树的结构进行调整,来满足红黑树的性质。
在博文http://blog.csdn.net/zhongjiekangping/archive/2010/05/26/5624503.aspx中对红黑树插入的情况做了详细的描述。
将下面函数对比上三幅图即可。
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
struct rb_node *parent, *gparent; --一个为父节点,一个为祖父节点
while ((parent = rb_parent(node)) && rb_is_red(parent)) --从node获得父节点指针值,并判断父节点是否为红色
{
gparent = rb_parent(parent);
if (parent == gparent->rb_left)
{
{
register struct rb_node *uncle = gparent->rb_right;
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
if (parent->rb_right == node)
{
register struct rb_node *tmp;
__rb_rotate_left(parent, root);
tmp = parent;
parent = node;
node = tmp;
}
rb_set_black(parent);
rb_set_red(gparent);
__rb_rotate_right(gparent, root);
} else {
{
register struct rb_node *uncle = gparent->rb_left;
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
if (parent->rb_left == node)
{
register struct rb_node *tmp;
__rb_rotate_right(parent, root);
tmp = parent;
parent = node;
node = tmp;
}
rb_set_black(parent);
rb_set_red(gparent);
__rb_rotate_left(gparent, root);
}
}
rb_set_black(root->rb_node);
}
在理解红黑二叉树后,再来理解内存管理。在linux中虚拟内存的vma采用红黑树的结构来管理。这也是为什么要去理解红黑树的结构。
二.虚拟内存管理
在start_kernel中有一段关于vma的初始化
vmalloc_init -> __insert_vmap_area
将已有的vma添加入管理。
static void __insert_vmap_area(struct vmap_area *va)
{
struct rb_node **p = &vmap_area_root.rb_node;
struct rb_node *parent = NULL;
struct rb_node *tmp;
while (*p) { --查询适合的插入点
struct vmap_area *tmp;
parent = *p;
tmp = rb_entry(parent, struct vmap_area, rb_node);
if (va->va_start < tmp->va_end)
p = &(*p)->rb_left;
else if (va->va_end > tmp->va_start)
p = &(*p)->rb_right;
else
BUG();
}
rb_link_node(&va->rb_node, parent, p); --将节点插入
rb_insert_color(&va->rb_node, &vmap_area_root); --调整红黑二叉树。
tmp = rb_prev(&va->rb_node);
if (tmp) {
struct vmap_area *prev;
prev = rb_entry(tmp, struct vmap_area, rb_node);
list_add_rcu(&va->list, &prev->list);
} else
list_add_rcu(&va->list, &vmap_area_list);
}
上面是vmalloc_init。
 爱华网
爱华网