余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理。运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题。
基本信息
中文名称
余弦定理
外文名称
cos
目录
展开
1 基本简介
2 数学应用
2.1 求边
2.2 求角
3 定理证明
3.1 平面向量证法
3.2 平面几何证法
4 相关应用
1 基本简介
余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。是勾股定理在一般三角形情形下的推广。高中阶段,余弦定理是比较重要的数学公式。
余弦定理
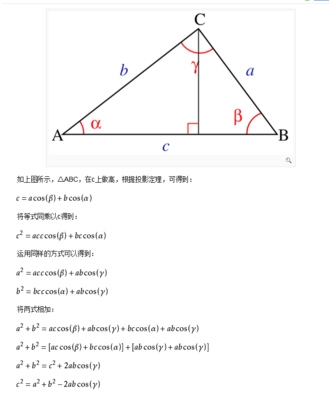
如图所示,△ABC,余弦定理可表示为:
a^2=b^2+c^2--2bc cos A,
同理,也可描述为:
b^2=a^2+c^2--2ac cos B,
c^2=a^2+b^2--2ab cos C
变式:
2a=2b+2c-2bc cos A==>2a=2(b+c-bc cos A)——a=b+c-bc co sA
其他同理。
cos A=b^2+c^2-a^2/2bc
其他同理。
2 数学应用
余弦定理是解三角形中的一个重要定理,可应用于以下两种需求:
当已知三角形的两边及其夹角,可由余弦定理得出已知角的对边。
当已知三角形的三边,可以由余弦定理得到三角形的三个内角。
2.1 求边
余弦定理公式可变换为以下形式:
如果知道了三角形的两边及其夹角,可由余弦定理得出已知角的对边。
2.2 求角
余弦定理公式可变换为以下形式:
因为余弦函数在 上的单调性,可以得到:
因此,如果已知三角形的三条边,可以由余弦定理得到三角形的三个内角。
3 定理证明
3.1 平面向量证法
∵如图,有 a+ b= c (平行四边形定则:两个邻边之间的 对角线代表两个邻边大小)∴ c· c=(a+ b)·( a+ b)
∴ c^2= a· a+2 a· b+ b· b∴ c^2= a^2+ b^2+2| a|| b| Cos(π-θ)(以上粗体字符表示向量)
又∵c os(π-θ)=-Cosθ
∴c^2=a^2+b^2-2|a||b|c osθ(注意:这里用到了 三角函数公式)
再拆开,得c^2=a^2+b^2-2*a*b* CosC
即 c osC=(a^2+b^2-c^2)/2*a*b
同理可证其他,而下面的c osC=(a^2+b^2-c^2)/2ab就是将c osC移到左边表示一下。
3.2 平面几何证法
在任意△ABC中 余弦定理
做AD⊥BC.
∠C所对的边为c,∠B所对的边为b,∠A所对的边为a
则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c
根据 勾股定理可得:
AC2=AD2+DC2
b2=(sinB*c)2+(a-cosB*c)2
b2=(sinB*c)2+a2-2ac*cosB+(cosB*c)2
b2=(sinB^2+cosB^2)*c2-2ac*cosB+a2
b2=c2+a2-2ac*cosB
begin{displaymath} cosB=(c2+a2b2)~2*a*c end{displaymath}
()
4 相关应用
在实际生活中,余弦定理是在计算机应有技术中的智能推荐系统,新闻分类中的基本算法之一。从吴军的《数学之美》那本书上知道余弦公式是可以对新闻进行分类的,当然就可以用来对用户进行分类了。引用《数学之美》文章中的话:“向量实际上是多维空间中有方向的线段。如果两个向量的方向一致,即夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,这就要用到余弦定理计算向量的夹角了。” “当两条新闻向量夹角的余弦等于一时,这两条新闻完全重复(用这个办法可以删除重复的网页);当夹角的余弦接近于一时,两条新闻相似,从而可以归成一类;夹角的余弦越小,两条新闻越不相关。 ”同理,可以在推荐系统中用来计算用户或者商品的相似性。
数学定理 15定理 2π定理 Sun-Ni定理 Vizing定理 阿贝尔定理
阿贝尔二项式定理 阿贝尔-鲁菲尼定理 阿贝尔曲线定理 阿达马三圆定理 阿蒂亚-辛格指标定理
阿尔泽拉-阿斯科利定理 阿基米德原理 阿基米德中点定理 埃尔布朗定理 艾森斯坦定理
安达尔定理 奥尔定理 巴拿赫不动点定理 巴拿赫-塔斯基悖论 贝尔纲定理
贝亚蒂定理 贝叶斯定理 贝祖定理 本迪克森-杜拉克定理 本原元定理
闭图像定理 波尔查诺-魏尔斯特拉斯定理 伯恩斯坦定理 伯特兰-切比雪夫定理 博苏克-乌拉姆定理
博特周期性定理 不动点定理 布尔素理想定理 布朗定理 布劳威尔不动点定理
布列安桑定理 采样定理 陈氏定理 垂径定理 达布中值定理
大数定律 代数基本定理 单调收敛定理 单值化定理 等周定理
狄利克雷定理 迪尼定理 笛卡儿定理 笛卡儿符号法则 笛沙格定理
棣莫弗定理 棣莫弗-拉普拉斯定理 多项式定理 多项式余数定理 二次互反律
二项式定理 法图引理 法伊特-汤普森定理 凡·奥贝尔定理 反函数定理
范德瓦尔登定理 费马大定理 费马多边形数定理 费马平方和定理 费马小定理
芬斯勒-哈德维格尔定理 弗罗贝尼乌斯定理 辐角原理
富比尼定理 高斯-卢卡斯定理 高斯-马尔可夫定理 高斯散度定理 哥德巴赫-欧拉定理
哥德尔不完备定理 哥德尔完备性定理 鸽巢原理 格尔丰德-施奈德定理 格林公式
共轭复根定理 勾股定理 古尔丁定理 古斯塔夫森定理 谷山-志村定理
哈恩-巴拿赫定理 海涅-博雷尔定理 海涅-康托尔定理 亥姆霍兹定理 赫尔德定理
黑林格-特普利茨定理 胡尔维兹定理 蝴蝶定理 华勒斯-波埃伊-格维也纳定理 霍普夫-里诺定理
积分第二中值定理 积分第一中值定理 基尔霍夫定理 吉洪诺夫定理 极值定理
夹挤定理 嘉当-迪厄多内定理 角平分线定理 介值定理 紧致性定理
卷积定理 绝妙定理 卡迈克尔定理 卡诺定理 开世定理
开映射定理 凯莱定理 凯莱-哈密顿定理 戡根定理 康托尔-伯恩斯坦-施罗德定理
康托尔定理 柯西定理 柯西积分定理 柯西-利普希茨定理 柯西中值定理
可靠性定理 克莱姆法则 克莱尼不动点定理 克罗内克定理 克罗内克-韦伯定理
克纳斯特-塔斯基定理 空间分割定理 拉东-尼科迪姆定理 拉格朗日定理 拉格朗日定理
拉格朗日中值定理 拉克斯-米尔格拉姆定理 拉姆齐定理 勒贝格控制收敛定理 勒贝格微分定理
勒让德定理 勒文海姆-斯科伦定理 雷维收敛定理 黎曼级数定理 黎曼-勒贝格定理
黎曼-罗赫定理 黎曼映射定理 里斯表示定理 良序定理 林德曼-魏尔斯特拉斯定理
零一律 刘维尔定理 留数定理 六指数定理 卢津定理
吕利耶定理 罗尔定理 罗斯定理
马勒定理 迈尔斯定理 迈希尔-尼罗德定理 毛球定理 梅涅劳斯定理
米迪定理 密克定理 闵可夫斯基定理 莫尔-马歇罗尼定理 莫雷角三分线定理
莫雷拉定理 拿破仑定理 纳什嵌入定理 鸟头定理 牛顿定理
欧几里得定理 欧拉定理 欧拉定理 欧拉旋转定理 帕普斯定理
帕塞瓦尔定理 帕斯卡定理 排容原理 庞加莱-本迪克松定理 庞加莱-霍普夫定理
披萨定理 皮卡定理 皮克定理 皮亚诺存在性定理 婆罗摩笈多定理
普罗斯定理 谱定理 齐肯多夫定理 切除定理 切消定理
曲线基本定理 儒歇定理 若尔当曲线定理
萨维奇定理 塞瓦定理 三次互反律 射影定理 施图姆定理
舒尔正交关系 斯坦纳-雷姆斯定理 斯通布尔代数表示定理 斯图尔特定理 斯托尔兹-切萨罗定理
斯托克斯定理 四顶点定理 四平方和定理 四色定理 素数定理
算术基本定理 泰博定理 泰勒公式 泰勒斯定理 泰勒中值定理
同构基本定理 图厄定理 图兰定理 托勒密定理 威尔逊定理
微积分基本定理 韦伯定理 韦达定理 维纳一辛钦 维维亚尼定理
魏尔施特拉斯分解定理 魏尔斯特拉斯逼近定理 沃尔斯滕霍尔姆定理 无限猴子定理 五边形数定理
五色定理 西尔维斯特惯性定理 西尔维斯特—加莱定理 西罗定理 西姆松定理
线性代数基本定理 线性同余定理 演绎定理 叶戈罗夫定理 因式定理
隐函数定理 友谊定理 有理根定理 有限简单群分类 有噪信道编码定理
余弦定理 圆幂定理 詹姆斯定理 正切定理 正弦定理
秩-零化度定理 中国剩余定理 中线定理 中心极限定理 中值定理
主轴定理 祖暅原理 最大流最小割定理 最大模原理
词条标签: 余弦 定理公式
 爱华网
爱华网