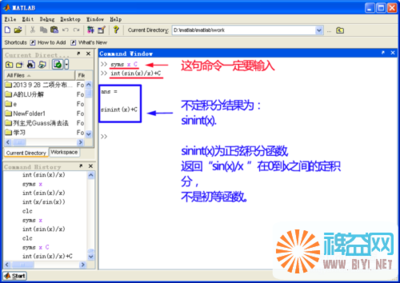
由于有不少的微积分等式无解析解存在,所以必须以数值方法求解。MATLAB提供了一些函数用来求微积分的数值解。
MATLAB提供最简单的积分函数是梯形法trapz,它的格式是trapz(x,y),其中x,y分别代表数目相同的数组或矩阵,而y与x的关系可以是连续的函数形态(如y=sin(x)),也可以是以点的方式描述的离散形态,下面给出实例:
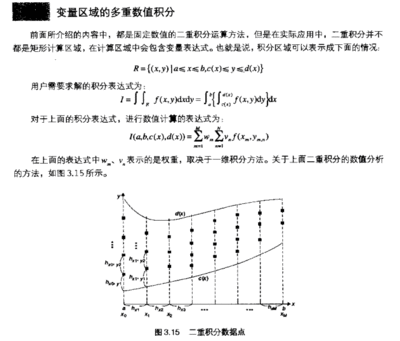
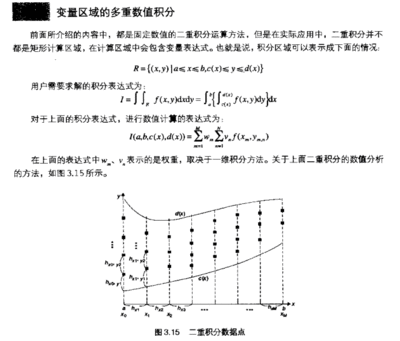
若用MATLAB梯形法来求:
>>x=0:pi/100:pi;%给出x的积分范围
>>y=sin(x);%描述y与x的函数关系
>>k=trapz(x,y)%求出定积分值k=1.9998
MATLAB另外提供有辛普森法(quad、quad8)的两种方法,计算精度按trapz、quad、quad8的顺序由低至高。辛普森法的格式是quad('function',a,b)(quad8语法相同),其中function是已定义的函数名,而a,b是积分的下限和上限。下面给出实例:
>>x=-1:0.07:2;%给出x的范围
>>y=humps(x);%y是x的humps函数
>>area=trapz(x,y);%用梯形法求得的结果是26.6243
>>area=quad('humps',-1,2);%直接用辛普森法,结果是26.3450
 爱华网
爱华网