1. 在计算机里,通常用数字后面紧跟一个英文字母来表示该数的数字,
十进制一般用D,二进制用B,八进制用O,十六进用H来表示,
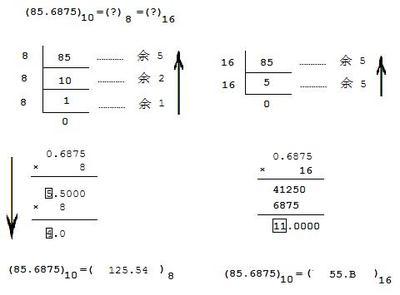
2.首先,十进制数转换成二进制,除2取余,按箭头方向写,自上而下写出来,所以45D转换成二进制为:101101B
3.十进制数转换成十六进除16取余,16进制一般用0~9,A,B,C,D,E,F,所以,117D转换成十六进制为:75H,
6.2 十六进制到二进制:每一位用4位二进制数来表示,最终形成对应的二进制数,如:
A19CH:A=10(十进制)=1010 ,1 = 0001 ,9 = 1001,C = 12(十进制)=1100,
所以A19CH =1010000110011100B
7.机器数
通常,机器数是把符号"数字化"的数,是数字在计算机中的二进制表示形式。
一:
数的符号数值化。实用的数据有正数和负数,由于计算机内部硬件只能表示两种物理状态(用0和1表示),因此实用数据的正号“+”或负号“-”,在机器里就用一位二进制的0或1来区别。通常这个符号放在二进制数的最高位,称符号位,以0代表符号“+”,以1代表符号“-”。因为有符号占据一位,数的形式值就不等于真正的数值,带符号位的机器数对应的数值称为机器数的真值。例如二进制真值数-011011,它的机器1011011。
二:
二进制的位数受机器设备的限制。机器内部设备一次能表示的二进制位数叫机器的字长,一台机器的字长是固定的。字长8位叫一个字节(Byte),现在机器字长一般都是字节的整数倍,如字长8位、16位、32位、64位。
三:
机器数可以用不同的码制来表示,常用的有原码,补码,和反码表示法。
将数的真值形式中“+”号用“0”表示,“-”号用“1”表示时,叫做数的原码形式,简称原码。若字长为n位,原码一般可表示为:
(1)当X为正数时[X]原和X一样,即[X]原 =X。当X为负数时。由于X本身为负数,所以,实际上是将∣X∣数值部分绝对值前面的符号位上写成“1”即可。
原码表示法比较直观,它的数值部分就是该数的绝对值,而且与真值、十进制数的转换十分方便。但是它的加减法运算较复杂。当两数相加时,机器要首先判断两数的符号是否相同,如果相同则两数相加,若符号不同,则两数相减。在做减法前,还要判断两数绝对值的大小,然后用大数减去小数,最后再确定差的符号,换言之,用这样一种直接的形式进行加运算时,负数的符号位不能与其数值部分一道参加运算,而必须利用单独的线路确定和的符号位。要实现这些操作,电路就很复杂,这显然是不经济实用的。为了减少设备,解决机器内负数的符号位参加运算的问题,总是将减法运算变成加法运算,也就引进了反码和补码这两种机器数。
4.2 反码
如前所述,为了克服原码运算的缺点,采用机器数的反码和补码表示法。若字长为n位,反码可表示为:
(2)即对正数来说,其反码和原码的形式相同;对负数来说,反码为其原码的数值部分各位变反。
4.3 补码
补码是根据同余的概念引入的,我们来看一个减法通过加法来实现的例子。假定现在是北京时间6点整,有一只手表却是8点整,比北京时间快了2小时,校准的方法有两种,一种是倒拨2小时,一种是正拨10小时。若规定倒拨是做减法,正拨是做加法,那么对手表来讲减2与加10是等价的,也就是说减2可以用加10来实现。这是因为8加10等于18,然而手表最大只能指示12,当大于12时12自然丢失,18减去12就只剩6了。这说明减法在一定条件下,是可以用加法来代替的。这里“12”称为“模”,10称为“-2”对模12的补数。推广到一般则有:
A – B = A + ( – B + M ) = A + ( – B)补
总之,正数的原码、反码和补码是完全相同的;负数的原码、反码和补码其形式各不相同。另外,特别要注意的是,对于负数的反码和补码(即符号位为1的数),其符号位后边的几位数表示的并不是此数的数值。如果要想知道此数的大小,一定要求其反码或补码才行。
多数机器里面都是采用补码表示,正数采用符号+绝对值表示,如:假设机器字长为8位,则[+1]补 =00000001,[+127]补=01111111,[+0]补=00000000,当用补码表示法表示负数时,负数X用2的n次方-[X]来表示,其中n为机器的字长。如:[-1]补= 28-1 = 11111111,[-127]补 =28-127=256-127=129=1000001,0的补码就只有一种表示法:八个0,00000000.
对于10000000这个数,在补码表示法中被定义为-128,采用补码形式表示的有符号数,那么n位二进制数据能够表示的有符号整数的范围是:-2(n-1)~2(n-1)-1是n-1次方(我现在能够理解补码了,也能理解这个范围了,我以前好像陷入了一个这种误解,老是以为这个范围,是这样得出的,比如,负数,最高位是1,对于机器字长8位来说,剩余的七位全是1,即1111111,加起来,就是八个11111111,然后,最小的就是8个0,00000000,然后把这个数转换成相应的十进制,就是范围,其实,我理解错了,为什么呢,这里的所谓的11111111是补码,而我把补码的表示当成了原码的表示来转换成十进制,这就是错误的根源,说明我以前是没理解补码和原码的区别)
那么,8位表示的有符号数的范围是:-128~127,如果n=16,那么能够表示的有符号数整数的范围是-32768~32767(记住这个范围)
例如,假设机器字长是16位,写出-117D的补码表示:
-117D = 216-117D 我把每个数都转化成2进制,也就是1 00000000 0000 0000 – 0000 0000 0111 0101 = 1111 1111 1000 1011这个数转换成六进制就是 FF8BH。
我采用书上的解法就是:
首先:+117D可表示为: 0000 0000 0111 0101
按位求反后为 1111 11111000 1010
某位加1 后: 1111 11111000 1011
表示成十六进制: F F 8 B(最终结果)
如果,对于无符号数来说,8位无符号数的表示范围:0<=n<=2的n次方-1,即:0~255
16位无符号数的表示范围:0<=n<=2n的n次方-1,即:0~65535(也要记住)

符号扩展,常需要把一个n位二进制数扩展为m位二进制数,(m>n),当要扩充的数十无符号数时,只要在最高位前扩展m-n个0,例如,21的8位二进制和16位二进制的补码表示如下:000101018位, 0000000000010101 16位
如果要扩展的数是有符号数,并且采用补码形式表示,进行符号扩展,如:-3的8位二进制补码和16位二进制补码如下:-3 1111 11018位补码,1111 1111 1111 1101 16位补码,
补码的加法和减法
把一个二进制按位求反,末位加1的运输称为求补运算。求补运算有个特性,[X]补---》求补[-x]补--à求补[X]补,就是,比如,3的补码表示是:00000011,这个数求补:11111101-3,对-3再求补,就变成了00000011,则又变成了整数3,
例如:用8位二进制计算,25+(-32)
我们用求补码的方式来解决这个问题,25是整数,他的补码为:00011001,
(-32)的补码是:先求32的补码:00100000,对它求反:11011111,末尾加1,得:11100000,然后把它与25的补码00011001相加得11111001,这个数最高位为1,肯定是个负数,我们对这个数求反再末尾加1,得00000111,刚好为7,根据补码的那个求补特性,[X]补---》求补[-x]补--à求补[X]补,所以11111001就是-7,跟我们用十进制算出来的结果一样。
 爱华网
爱华网