曹泽新
一题外话
因为要集中精力研究经济和专业工作,这里就把个人关于四色问题和hadwiger猜想的证明存这里备档,做个了结,不再摆弄它了。
1.证明四色问题的直接原因,是因为那个计算机证明一直TM折磨着我。个人实在从观念上无法接受计算机证明,所以才尝试证明四色问题,而不是要证明自己在数学上有什么天赋,相反,本证明是承认他人在这方面的工作中获得的。
2.本证明从一开始就接受了别人的教训,别人已经走过而走不通的路,肯定走不通,我早早就告诫自己,不要重蹈他人覆辙,千万别脑残到要和那些大数学家叫板的程度。
3. 文献《数学的陷阱——四色猜想的各种“证明”》(链接地址:http://www.cnki.net/KCMS/detail/detail.aspx?dbcode=cjfq&dbname=cjfd1991&filename=zrzz199105013)中各种错误证明,基本可以表明图论模式证明四色问题的思路,肯定走不通。通过这些错误证明,我判断图论方法很可能不可行,不要对偶图,要回到问题的起点——原汁原味的地图上来。这里也已经暗示四色问题很可能不是图论问题。
4.那些所谓四色问题的归纳法证明,显然没有理解四色问题的整体性,用这些同样来证明环形是3着色的,都不好使,因为奇数顶点的环形可以永远最后一个顶点着第三色。
5. 本证明1997年就有了,2003年在arxiv.org上给出预印本(http://arxiv.org/abs/math/0311475),因为别的原因,没有捣鼓它,就一直放到现在。
6.本文中的证明简洁直观,但不算非常简单,理解需要有拓扑空间概念和一定的空间想象力,而且还要求一点点逻辑思维能力,基本上理工科本科以外的,建议不要费力气理解。
二这一证明中的思想方法
1.把四色问题简化成由顶点和边组成的图论问题,是对证明四色问题的最大误导,四色问题一开始是平面上的地图问题,是一种拓扑空间的拓扑性质问题,而不是离散数学中的图论问题。也就是说,以前的证明者从一开始就被坑了,他们的思维一开始就忽忽悠悠地,被拐到图论中的边和顶点的关系问题上。结果导致平面四色问题,似乎只能通过点边关系来证明,相当坑爹。
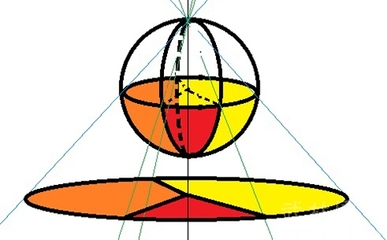
2.图论和拓扑空间问题的最大差别在于,地图是一种连续空间分布,可以是三维空间或三维物体的一个截面,而图论中被简化的平面图只剩下渣渣,截不了面,平面图和它的N色几何生成元之间的关系就根本没有办法通过这种截面的方式表达出来,也就是下图Figure3中的第4个截面关系,在图论中只能是关系6,没办法表达它们之间的生成关系。
3.如果平面是4着色的,那么任一个4色平面地图,可以是四种不同颜色两两相邻的橡皮泥揉搓拉扯,然后截面获得。5色的情况也一样。而要获得这种可以截取相应平面地图的4色或者5色橡皮泥,你完全可以反过来,把平面图变厚,然后用同种颜色的橡皮棒棒把同色的地图粘连成一体,然后充气或者灌浆把空间占满,这种4色或5色橡皮泥就搞定了。也就是下图Figure3中的第4个关系,我们可以通过上面的方法反过来构造三维的K4。
4.任意五个国家不能两两相邻,是平面的性质,并被平面图继承。而平面的这种性质,实际上是一种拓扑空间的性质,这种拓扑空间中,任意N+1个区域不能两两相邻,如直线、圆环、平面都有这类性质。我称之为N度分裂拓扑空间,这个名字感觉不太好,似乎叫色空间更合适些,色即是空,空即是色嘛。
5.三维空间中可以有任意个区域两两相邻,不是上面所说的这种空间。但是证明的最关键就在这里:我们可以抽象出这样一种三维空间,其中任意5个区域不能两两相邻,其它方面和三维空间一样。
6.有些善良的同志会怀疑这种三维空间的存在性,但考虑到平面就是这样一种空间,所以这种三维空间不仅可以抽象出来,平面还必然是其截面。证明很简单,将平面地图沿Z轴无限延伸,这种4度三维分裂拓扑空间的一个比较单调的分布就搞定了,而那个平面地图显然就是其截面。论文中Figure5就是一种任意三个区域不能两两相邻的2度二维分裂拓扑空间的表示。Figure 6则通过1维和2维的关系,说明本段内容。
7.这一空间是证明的最最关键部分,也是本证明中本人的得意之笔,这里称之为分裂拓扑空间,它同时具有离散和连续的性质,而且这两种性质还无不干扰。不过有些同志难以想象,有些同志接受不了,这两种同志,想想平面就能接受这种空间了。
8.这样,证明就极其简单了,平面之所以是4着色的,因为平面是这种4度三维拓扑空间的截面,而这种4度三维空间又把5色橡皮泥这种五色地图的生成元挡在外面。换句话说,三维的5色橡皮泥块,要想放到这种三维空间中,其中至少有两块不同颜色的橡皮泥的相邻关系断开,这样5色橡皮泥就必然变成四色橡皮泥,截面中的相应相邻关系也必然断开。这样,躲在三维4度分裂拓扑空间下的平面,其上的平面图怎么可能还需要5色呢,4色搞定。
9. 本证明中不需要用到平面图的K(3,3)条件,这是本证明方法相对图论方法的先天优势。
10. 看似更复杂的hadwiger猜想,仅仅是本证明在高维空间中的一个平凡推论。
 爱华网
爱华网