哈希表也称散列表,是一种数据结构,在JAVA集合中的HASHMAP,HASHTABLE都运用了哈希表.
它可以提供快速的插入操作和查找操作,不论有多少数据项,插入与删除只需要接近常量的时间:O(1)时间级.
在计算机程序中,如果需要在一秒种内查找上千条记录,通常使用哈希表.
哈希表的速度明显比树快.树的操作通常需要O(N)的时间级.哈希表不仅速度快,而且编程实现也相对容易.
但哈希表也有缺点,它是基于数组的,数组一旦被创建,就难以扩展.某些哈希表被填满时,性能急剧下降.,所以程序员必须清楚表中要存储多少数据.
哈希表操作的平均时间是基于统计特性而不是随机输入的期望值.
哈希表的重要特性就是哈希函数.
我们用一个将大数(或解释为数的字符串)映射成一个较小的,更容易管理的数的函数来达到这个目的.
将一个项映射成一个较小的下标的函数称为哈希函数.
需要哈希函数,是因为哈希表是基于数组的,而且关键字值的范围通常比数组容量大.,关键字值通过哈希函数映射为数组的下标.
在JAVA中,通过取模运算来实现.arrayIndex=hugeNumber%smallRange,这就是一个简单的哈希函数.
哈希函数简化了操作,但也带来了不可避免的麻烦:两个或更多的不同项可能被散列到同一个位置,引起冲突.
哈希函数不仅要容易计算,而且要对键值的分布要均匀.如果有太多的冲突,哈希表的性能将显著下降.
对于下面的哈希函数:
public static inthash(String key , int tableSize){ int hashVal = 0; for(int i=0;i<key.length;i++){ hashVal+=key.charAt(i); } returnhashVal%tableSize; } |
这个哈希函数很简单,很容易实现,计算哈希值也非常快,但这是个糟糕的哈希函数.
假设tableSize很大,为10000,再假设所有的关键字值的长度都是8个或少于8个字符.因为一个ASCIIchar是一个0到127之间的整数,那么哈希函数的值介于0到1016(127*8)之间,这个限制肯定不会产生一个均匀的分布.
为了减少冲突:
1.开放地址法
2.链地址法
开放地址法:
让指定的数组大小两倍于需要存储的数据量.
因此,可能一半的单元是空的.当冲突发生时,一个方法是通过系统的方法找到数组的一个空位,并把这个单词填入,而不再用哈希函数得到的数组下标.
链地址法:
创建一个存放单词链表的数组,数组内不直接存储单词.这样,当发生冲突的时候,新的数据项直接接到这个数组下标所指的链表中.
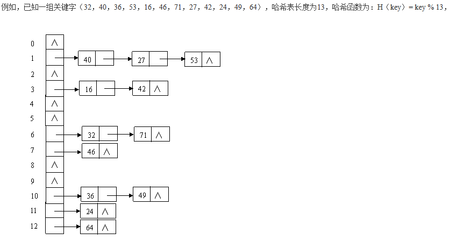
开放地址法
在开放地址法中如果数据不能直接放在由哈希函数中,就得寻找空白位置,其中有简单的三种探索方法.
线性探索法,二次探索法,再哈希法.
线性探索法:就是当通过哈希函数找到的位置有冲突时,再沿着数组下标递增向下探测,例如:寻找到1002置,但已经有数据,就向1003,1004….寻找.
当哈希表越来越满的时候,哈希表的性能就会严重降低.并且填充序列越来越长,这种现象称为聚集.
哈希表的容量总是选一个质数.这可以使数据均匀分布.因为哈希函数是以表长为模运算.
例如,表长为15(下标0到14),有一特定的下标0,步长为5,那么只能是0,5,10,0,5,10….以此类推,一直循环下去.只探索到三个单元.表长为13,就会有0,5,10,2,7,12,4,一直下去,只要表中有一空位,就一直探测下去,由于任何数想整除它都是不可能的,所以会探测到所有单元.
如果哈希表越来越满,都必须扩展数组,而且不能简单的把旧数组中的数据一一拷贝到新数组的相应位置,因为数据项的位置是由数组的长度计算而来的.所以必须重新按照哈希函数给定数据项的位置.这也就是重新哈希化.这是一个耗时的过程.
为了降低聚集,运用二次探索法,已填入哈希表的数据项和表长的比率叫做装填因子.当装填因子不太大的时候,聚集分布得比较连贯,哈希表中可能一部分有大量的聚集,而另一部分比较稀疏.聚集降低了哈希表的性能.
二次探索法的思想就是探测相隔较远的单元,而不是线性探测的相邻的单元.
如果数组下标为x,在线性探测中,是x+1,x+2,x+3…..而在二次探测中,是步数的平方,x+ ,x+ .....
如果表的大小为素数且负载因子不大于0.5,所有的探测将会到达不同的单元,项总是能被插入的.
一旦负载因子到达0.5就得立刻扩展数组.
在二次探索法中也有二次聚集现象,但二次聚集只是一个很小的理论缺陷.
为了消除原始聚集及二次聚集现象,可以用再哈希法也称双重散列,原始聚集及二次聚集的原因是因为它们的探测步长都是固定的.
现在找到产生一种依赖于关键字的探测序列,而不是每个关键字都一样.这样即使有关键字被映射到同一个数组下标,也可以有不同的探测序列.
方法是把关键字用不同的哈希函数再做一次哈希化.这个结果作为步长.对于指定的关键字,步长在整个探测过程中都是不变的,不过不同的关键字使用不同的步长.
第二个哈希函数必须符合以上两个要求:
1.和第一个哈希函数不一样
2.不能输出0,否则将没有步长,每次探测将是原地踏步,算法将无法进行.
专家发现以下哈希函数形式很好:
stepSize = constant– (key % constant ) 其中constant为质数,并且小于数组容量.
链地址法
在开放地址法中,寻找一个减少冲突的方法,
在链地址法中,数据项的关键字值还是映射到数组下标,而数据本身保存在每个单元的链表中.
此方法概念上去开放地址法简单,但代码相对复杂,因为它涉及到链表机制.
此方法中的装填因子不同于开放地址法,因为哈希表中N个单元要存储N个或更多的数据项.装填因子一般为1,或大于1.
当然如果链表中有许多项,存取时间变长,找到初始单元的时间为O(1),而搜索链表的时间与链表中的数据项数目M成正比,为O(M).因此并不希望链表太满.
在开放地址法中,当装填因子超过二分之一或三分之二的时候,哈希表的性能就严重下降.在链地址法中,装填因子达到1以上,而且对性能没有多在影响,因此链地址法比开放地址法更键壮,尤其是不清楚要存储多少数据项的时候.
还有一种方法类似于链地址法,它在哈希表的每个单元用的是数组,而不是链表.这样的数组有时称为桶.这种方法并没有链地址法有效,因为桶容量不好选择.太小会溢出,太大浪费空间.
对于哈希函数的经验就是既简单又快,而且去掉关键字中的无用数据,并尽量全用关键字的所有数据.
在实际情况中,装填因子取决于存储速度与效率之间的平衡.装填因子变小,效率下降,但速度上升..
 爱华网
爱华网