发布时间:2018年04月10日 20:51:50分享人:江南过客来源:互联网10
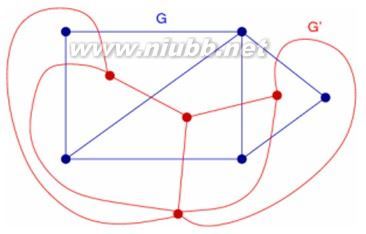
0 定义 一个图G=(V,E),若能将其画在平面上,且任意两条边的交点只能是G的顶点,则称G可嵌入平面,或称G是可平面的。可平面图在平面上的一个嵌入称为一个平面图。如下图左边黑色的图为平面图,右边红色的图不属于平面图:
由平面图的边包围而成,其中不含图的顶点。也称为面。包围面R的所有边组成的回路称为该面的边界,回路长度称为该面的度,记为deg(R)。具有相同边界的面称为相邻面。由平面图的边包围且无穷大的面称为外部面。一个平面图有且只有一个外部面。如下面的平面图中,R0是外部面R0与R1,R2, R3均相邻。deg(R0)=8, deg(R1)=4,deg(R2)=5(R2经过的顶点序列为v7-v4-v6-v4-v5-v7), deg(R3)=1:
利用欧拉公式和数学归纳法可以证明平面图G的所有面的度之和等于其边数|E|的2倍,即:下面我们引入对偶图,设有平面图G=(V,E),满足下列条件的图G'=(V',E')称为图G的对偶图:G的任一面Ri内有且仅有一点Vi';对G的域Ri和Rj的共同边界Ek,画一条边Ek'=(Vi',Vj')且只与Ek交于一点;若Ek完全处于Ri中,则Vi'有一自环Ek',如下图G'是G的对偶图:1 最大流的应用如果网络流中的图G可以转化为一个平面图,那么其对偶图G'中的环对应G中的割,利用最大流最小割定理转化模型,根据平面图G'与其对偶图的关系,先求出最小割。首先连接s和t,如下图蓝色虚线,得到一个附加面,我们设附加面对应的点为s',无界面对应的点为t',求该图的红色的对偶图G',最后删去s'和t'之间的边:
一条从s'到t'的路径,就对应了一个s-t割,更进一步,如果我们令每条边的长度等于它的容量,那么最小割的容量就等于最短路的长度。这样时间复杂度大大降低了。
爱华网本文地址 » http://www.aihuau.com/a/25101012/115178.html
更多阅读
内涵图的制作与使用——简介内涵图,不同于我们一般说的搞笑图片,而是真正的,图里面还包涵其它文件的“内涵”图。说白了,就是将一些不太想让别人知道的文件(如bt种子之类的)和一张图片合成为一张新的图片,原理和把多个文件压缩成一个压缩包

原文地址:总结DFN-LOW算法在图论中的应用作者:OIer_fc总结DFN-LOW算法在图论中的应用北京大学许若辰 长沙市雅礼中学 屈运华摘要: 在一个连通图[1]G中,有些点一旦被去除就会导致图不连通,同样的,有些边一旦被去除也会导致图G失去连通性,
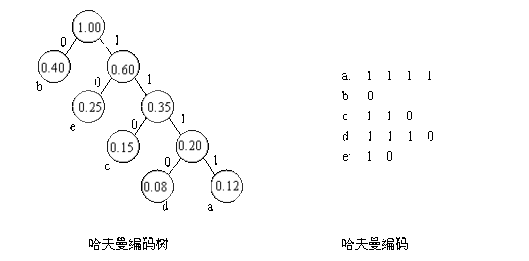
摘 要:字符编码与信息压缩是计算机应用的重要研究课题,许多学者对此作了很多非常有价值的研究。文章简单分析了二叉哈夫曼树的构造及编码,通过比较三种构造三叉哈夫曼树的算法,提出了构造任意K叉哈夫曼树及K进制的最优前缀编码的算法,并

首先我们需要知道计算机是以以矢量或位图格式来显示图形。 了解这两种格式的差别有助于您更有效地工作。 使用 Flash 可以创建压缩矢量图形并将它们制作为动画。 Flash 还可以导入和处理在其它应用程序中创建的矢量图形或位图图形。
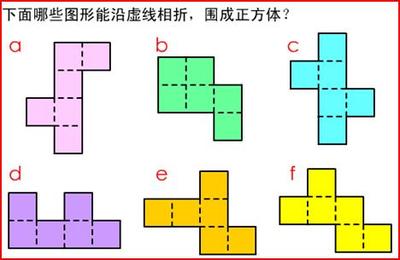
正方体的平面展开图的11种情形归纳一下有四种类型:即:1-4-1型2-3-1型2-2-2型3-3型反思:一个正方体的纸盒,至少要剪多少次才能展开成平面图形?为什么?

 爱华网
爱华网


