高中数学常用公式及结论 高中数学常用二级结论
2集合 的子集个数共有 个;真子集有 个;非空子集有 个;非空的真子集有 个.
3二次函数的解析式的三种形式:
(1)一般式 ;
(2)顶点式 ;(当已知抛物线的顶点坐标 时,设为此式)
(3)零点式 ;(当已知抛物线与 轴的交点坐标为 时,设为此式)
(4)切线式: 。(当已知抛物线与直线 相切且切点的横坐标为 时,设为此式)
4真值表:同真且真,同假或假
5常见结论的否定形式;
原结论
反设词
原结论
反设词
是
不是
至少有一个
一个也没有
都是
不都是
至多有一个
至少有两个
大于
不大于
至少有 个
至多有( )个
小于
不小于
至多有 个
至少有( )个
对所有 ,成立
存在某 ,不成立
或
且
对任何 ,不成立
存在某 ,成立
且
或
6四种命题的相互关系(下图):(原命题与逆否命题同真同假;逆命题与否命题同真同假.)
原命题 互逆 逆命题
若p则q 若q则p
互 互
互 为 为 互
否 否
逆 逆
否 否
否命题 逆否命题
若非p则非q 互逆 若非q则非p
充要条件:(1)、 ,则P是q的充分条件,反之,q是p的必要条件;
(2)、 ,且q≠>p,则P是q的充分不必要条件;
(3)、p≠>p,且 ,则P是q的必要不充分条件;
4、p≠>p,且q≠>p,则P是q的既不充分又不必要条件。
7函数单调性:
增函数:(1)、文字描述是:y随x的增大而增大。
(2)、数学符号表述是:设f(x)在x D上有定义,若对任意的 ,都有
成立,则就叫f(x)在x D上是增函数。D则就是f(x)的递增区间。
减函数:(1)、文字描述是:y随x的增大而减小。
(2)、数学符号表述是:设f(x)在x D上有定义,若对任意的 ,都有
成立,则就叫f(x)在x D上是减函数。D则就是f(x)的递减区间。
单调性性质:(1)、增函数+增函数=增函数;(2)、减函数+减函数=减函数;
(3)、增函数-减函数=增函数;(4)、减函数-增函数=减函数;
注:上述结果中的函数的定义域一般情况下是要变的,是等号左边两个函数定义域的交集。
复合函数的单调性:
函数单调
单调性
内层函数
↓
↑
↑
↓
外层函数
↓
↑
↓
↑
复合函数
↑
↑
↓
↓
等价关系:
(1)设 那么
上是增函数;
上是减函数.
(2)设函数 在某个区间内可导,如果 ,则 为增函数;如果 ,则 为减函数.
8函数的奇偶性:(注:是奇偶函数的前提条件是:定义域必须关于原点对称)
奇函数:
定义:在前提条件下,若有 ,
则f(x)就是奇函数。
性质:(1)、奇函数的图象关于原点对称;
(2)、奇函数在x>0和x<0上具有相同的单调区间;
(3)、定义在R上的奇函数,有f(0)=0.
偶函数:
定义:在前提条件下,若有 ,则f(x)就是偶函数。
性质:(1)、偶函数的图象关于y轴对称;
(2)、偶函数在x>0和x<0上具有相反的单调区间;
奇偶函数间的关系:
(1)、奇函数·偶函数=奇函数;(2)、奇函数·奇函数=偶函数;
(3)、偶奇函数·偶函数=偶函数;(4)、奇函数±奇函数=奇函数(也有例外得偶函数的)
(5)、偶函数±偶函数=偶函数;(6)、奇函数±偶函数=非奇非偶函数
奇函数的图象关于原点对称,偶函数的图象关于y轴对称;反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y轴对称,那么这个函数是偶函数.
9函数的周期性:
定义:对函数f(x),若存在T 0,使得f(x+T)=f(x),则就叫f(x)是周期函数,其中,T是f(x)的一个周期。
周期函数几种常见的表述形式:
(1)、f(x+T)=-f(x),此时周期为2T;
(2)、f(x+m)=f(x+n),此时周期为2 ;
(3)、 ,此时周期为2m。
10常见函数的图像:
11对于函数 ( ), 恒成立,则函数 的对称轴是 ;两个函数 与 的图象关于直线 对称.
12分数指数幂与根式的性质:
(1) ( ,且 ).
(2) ( ,且 ).
(3) .
(4)当 为奇数时, ;当 为偶数时, .
13指数式与对数式的互化式: .
指数性质:
(1)1、 ;(2)、 ( );(3)、
(4)、 ;(5)、 ;
指数函数:
(1)、 在定义域内是单调递增函数;
(2)、 在定义域内是单调递减函数。注:指数函数图象都恒过点(0,1)
对数性质:
(1)、 ;(2)、 ;
(3)、 ;(4)、 ;(5)、
(6)、 ;(7)、
对数函数:
(1)、 在定义域内是单调递增函数;
(2)、 在定义域内是单调递减函数;注:对数函数图象都恒过点(1,0)
(3)、
(4)、 或
14对数的换底公式: ( ,且 , ,且 , ).
对数恒等式: ( ,且 , ).
推论 ( ,且 , ).
15对数的四则运算法则:若a>0,a≠1,M>0,N>0,则
(1) ;(2) ;
(3) ;(4) 。
16平均增长率的问题(负增长时 ):
如果原来产值的基础数为N,平均增长率为 ,则对于时间 的总产值 ,有 .
17等差数列:
通项公式:(1) ,其中 为首项,d为公差,n为项数, 为末项。
(2)推广:
(3) (注:该公式对任意数列都适用)
前n项和:(1) ;其中 为首项,n为项数, 为末项。
(2)
(3) (注:该公式对任意数列都适用)
(4) (注:该公式对任意数列都适用)
常用性质:(1)、若m+n=p+q,则有 ;
注:若 的等差中项,则有2 n、m、p成等差。
(2)、若 、 为等差数列,则 为等差数列。
(3)、 为等差数列, 为其前n项和,则 也成等差数列。
(4)、 ;
(5)1+2+3+…+n=
等比数列:
通项公式:(1) ,其中 为首项,n为项数,q为公比。
(2)推广:
(3) (注:该公式对任意数列都适用)
前n项和:(1) (注:该公式对任意数列都适用)
(2) (注:该公式对任意数列都适用)
(3)
常用性质:(1)、若m+n=p+q,则有 ;
注:若 的等比中项,则有 n、m、p成等比。
(2)、若 、 为等比数列,则 为等比数列。
18分期付款(按揭贷款):每次还款 元(贷款 元, 次还清,每期利率为 ).
19三角不等式:
(1)若 ,则 .
(2)若 ,则 .
(3) .
20同角三角函数的基本关系式: , = ,
21正弦、余弦的诱导公式(奇变偶不变,符号看象限)
22和角与差角公式
; ;
.
=
(辅助角 所在象限由点 的象限决定, ).
23二倍角公式及降幂公式
.
.
.
24三角函数的周期公式
函数 ,x∈R及函数 ,x∈R(A,ω, 为常数,且A≠0)的周期 ;函数 , (A,ω, 为常数,且A≠0)的周期 .
三角函数的图像:
25正弦定理: (R为 外接圆的半径).
26余弦定理:
; ; .
27面积定理:
(1) ( 分别表示a、b、c边上的高).
(2) .
(3) .
28三角形内角和定理:
在△ABC中,有
.
29实数与向量的积的运算律:设λ、μ为实数,那么:
(1)结合律:λ(μ )=(λμ) ;
(2)第一分配律:(λ+μ) =λ +μ ;
(3)第二分配律:λ( + )=λ +λ .
30 与 的数量积(或内积): · =| || | 。
31平面向量的坐标运算:
(1)设 = , = ,则 + = .
(2)设 = , = ,则 - = .
(3)设A ,B ,则 .
(4)设 = ,则 = .
(5)设 = , = ,则 · = .
32两向量的夹角公式:
( = , = ).
33平面两点间的距离公式:
= (A ,B ).
34向量的平行与垂直:设 = , = ,且 ,则:
|| =λ .(交叉相乘差为零)
( ) · =0 .(对应相乘和为零)
35线段的定比分公式:设 , , 是线段 的分点, 是实数,且 ,则
( ).
36三角形的重心坐标公式:△ABC三个顶点的坐标分别为 、 、 ,则△ABC的重心的坐标是 .
37三角形五“心”向量形式的充要条件:
设 为 所在平面上一点,角 所对边长分别为 ,则
(1) 为 的外心 .
(2) 为 的重心 .
(3) 为 的垂心 .
(4) 为 的内心 .
(5) 为 的 的旁心 .
38常用不等式:
(1) (当且仅当a=b时取“=”号).
(2) (当且仅当a=b时取“=”号).
(3)
(4) .
(5) (当且仅当a=b时取“=”号)。
39极值定理:已知 都是正数,则有
(1)若积 是定值 ,则当 时和 有最小值 ;
(2)若和 是定值 ,则当 时积 有最大值 .
(3)已知 ,若 则有
。
(4)已知 ,若 则有
40一元二次不等式 ,如果 与 同号,则其解集在两根之外;如果 与 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.即:
;
.
41含有绝对值的不等式:当a>0时,有
.
或 .
42斜率公式:
( 、 ).
43直线的五种方程:
(1)点斜式 (直线 过点 ,且斜率为 ).
(2)斜截式 (b为直线 在y轴上的截距).
(3)两点式 ( )( 、 ( )).
两点式的推广: (无任何限制条件!)
(4)截距式 ( 分别为直线的横、纵截距, )
(5)一般式 (其中A、B不同时为0).
直线 的法向量: ,方向向量:
44夹角公式:
(1) . ( , , )
(2) .( , , ).
直线 时,直线l1与l2的夹角是 .
45 到 的角公式:
(1) .( , , )
(2) .( , , ).
直线 时,直线l1到l2的角是 .
46点到直线的距离: (点 ,直线 : ).
47圆的四种方程:
(1)圆的标准方程 .
(2)圆的一般方程 ( >0).
(3)圆的参数方程 .
(4)圆的直径式方程 (圆的直径的端点是 、 ).
48点与圆的位置关系:点 与圆 的位置关系有三种:
若 ,则 点 在圆外;
点 在圆上; 点 在圆内.
49直线与圆的位置关系:直线 与圆 的位置关系有三种( ):
; ; .
50两圆位置关系的判定方法:设两圆圆心分别为O1,O2,半径分别为r1,r2, ,则:
;
;
;
;
.
51椭圆 的参数方程是 . 离心率 ,
准线到中心的距离为 ,焦点到对应准线的距离(焦准距) 。
过焦点且垂直于长轴的弦叫通经,其长度为: .
52椭圆 焦半径公式及两焦半径与焦距构成三角形的面积:
, ; 。
53椭圆的的内外部:
(1)点 在椭圆 的内部 .
(2)点 在椭圆 的外部 .
54椭圆的切线方程:
(1)椭圆 上一点 处的切线方程是 .
(2)过椭圆 外一点 所引两条切线的切点弦方程是 .
(3)椭圆 与直线 相切的条件是 .
55双曲线 的离心率 ,准线到中心的距离为 ,焦点到对应准线的距离(焦准距) 。过焦点且垂直于实轴的弦叫通经,其长度为: .
焦半径公式 , ,
两焦半径与焦距构成三角形的面积 。
56双曲线的方程与渐近线方程的关系:
(1)若双曲线方程为 渐近线方程: .
(2)若渐近线方程为 双曲线可设为 .
(3)若双曲线与 有公共渐近线,可设为
( ,焦点在x轴上, ,焦点在y轴上).
(4)焦点到渐近线的距离总是 。
57双曲线的切线方程:
(1)双曲线 上一点 处的切线方程是 .
(2)过双曲线 外一点 所引两条切线的切点弦方程是 .
(3)双曲线 与直线 相切的条件是 .
58抛物线 的焦半径公式:
抛物线 焦半径 .
过焦点弦长 .
59二次函数 的图象是抛物线:
(1)顶点坐标为 ;(2)焦点的坐标为 ;
(3)准线方程是 .
60直线与圆锥曲线相交的弦长公式
或
(弦端点A ,由方程 消去y得到
, 为直线 的倾斜角, 为直线的斜率, .
61证明直线与平面的平行的思考途径:
(1)转化为直线与平面无公共点;
(2)转化为线线平行;
(3)转化为面面平行.
62证明直线与平面垂直的思考途径:
(1)转化为该直线与平面内任一直线垂直;
(2)转化为该直线与平面内相交二直线垂直;
(3)转化为该直线与平面的一条垂线平行;
(4)转化为该直线垂直于另一个平行平面。
63证明平面与平面的垂直的思考途径:
(1)转化为判断二面角是直二面角;
(2)转化为线面垂直;
(3)转化为两平面的法向量平行。
64向量的直角坐标运算:
设 = , = 则:
(1) + = ;
(2) - = ;
(3)λ = (λ∈R);
(4) · = ;
65夹角公式:
设 = , = ,则 .
66异面直线间的距离:
( 是两异面直线,其公垂向量为 , 是 上任一点, 为 间的距离).
67点 到平面 的距离:
( 为平面 的法向量, , 是 的一条斜线段).
68球的半径是R,则其体积 ,其表面积 .
69球的组合体:
(1)球与长方体的组合体:长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长,正方体的棱切球的直径是正方体的面对角线长,正方体的外接球的直径是正方体的体对角线长.
(3)球与正四面体的组合体:棱长为 的正四面体的内切球的半径为
(正四面体高 的 ),外接球的半径为 (正四面体高 的 ).
70分类计数原理(加法原理): .
分步计数原理(乘法原理): .
71排列数公式: = = .( , ∈N*,且 ).规定 .
72组合数公式: = = = ( ∈N*, ,且 ).
组合数的两个性质:(1) = ;(2) + = .规定 .
73二项式定理 ;
二项展开式的通项公式 .
的展开式的系数关系:
; ; 。
74互斥事件A,B分别发生的概率的和:P(A+B)=P(A)+P(B).
个互斥事件分别发生的概率的和:P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
75独立事件A,B同时发生的概率:P(A·B)=P(A)·P(B).
n个独立事件同时发生的概率:P(A1·A2·…·An)=P(A1)·P(A2)·…·P(An).
76n次独立重复试验中某事件恰好发生k次的概率:
77数学期望:
数学期望的性质
(1) .(2)若 ~ ,则 .
(3)若 服从几何分布,且 ,则 .
78方差:
标准差: = .
方差的性质:
(1) ;
(2)若 ~ ,则 .
(3)若 服从几何分布,且 ,则 .
方差与期望的关系: .
79正态分布密度函数: ,
式中的实数μ, ( >0)是参数,分别表示个体的平均数与标准差.
对于 ,取值小于x的概率: .
80 在 处的导数(或变化率):
.
瞬时速度: .
瞬时加速度: .
81函数 在点 处的导数的几何意义:
函数 在点 处的导数是曲线 在 处的切线的斜率 ,相应的切线方程是 .
82几种常见函数的导数:
(1) (C为常数).(2) .(3) .
(4) . (5) ; .
(6) ; .
83导数的运算法则:
(1) .(2) .(3) .
84判别 是极大(小)值的方法:
当函数 在点 处连续时,
(1)如果在 附近的左侧 ,右侧 ,则 是极大值;
(2)如果在 附近的左侧 ,右侧 ,则 是极小值.
85复数的相等: .( )
86复数 的模(或绝对值) = = .
87复平面上的两点间的距离公式:
( , ).
88实系数一元二次方程的解
实系数一元二次方程 ,
①若 ,则 ;
②若 ,则 ;
③若 ,它在实数集 内没有实数根;在复数集 内有且仅有两个共轭复数根 .
高中数学公式提升
一、集合、简易逻辑、函数
1.研究集合必须注意集合元素的特征即三性(确定,互异,无序);已知集合A={x,xy,lgxy},集合B={0,|x|,y},且A=B,则x+y=
2.研究集合,首先必须弄清代表元素,才能理解集合的意义。已知集合M={y|y=x2,x∈R},N={y|y=x2+1,x∈R},求M∩N;与集合M={(x,y)|y=x2,x∈R},N={(x,y)|y=x2+1,x∈R}求M∩N的区别。
3.集合A、B, 时,你是否注意到“极端”情况: 或 ;求集合的子集 时是否忘记 .例如: 对一切 恒成立,求a的取植范围,你讨论了a=2的情况了吗?
4.对于含有n个元素的有限集合M,其子集、真子集、非空子集、非空真子集的个数依次为 如满足条件 的集合M共有多少个
5.解集合问题的基本工具是韦恩图;某文艺小组共有10名成员,每人至少会唱歌和跳舞中的一项,其中7人会唱歌跳舞5人会,现从中选出会唱歌和会跳舞的各一人,表演一个唱歌和一个跳舞节目,问有多少种不同的选法?
6.两集合之间的关系。
7.(CUA)∩(CUB)=CU(A∪B)(CUA)∪(CUB)=CU(A∩B); ;
8、可以判断真假的语句叫做命题.
逻辑连接词有“或”、“且”和“非”.
p、q形式的复合命题的真值表:(真且真,同假或假)
p
q
P且q
P或q
真
真
真
真
真
假
假
真
假
真
假
真
假
假
假
假
9、命题的四种形式及其相互关系 :
互 逆
互 互
互 为 互
否 逆 逆 否
否 否
否 否
否 互 逆
原命题与逆否命题同真同假;逆命题与否命题同真同假.
10、你对映射的概念了解了吗?映射f:A→B中,A中元素的任意性和B中与它对应元素的唯一性,哪几种对应能够成映射?
11、函数的几个重要性质:
①如果函数 对于一切 ,都有 或f(2a-x)=f(x),那么函数 的图象关于直线 对称.
②函数 与函数 的图象关于直线 对称;
函数 与函数 的图象关于直线 对称;
函数 与函数 的图象关于坐标原点对称.
③若奇函数 在区间 上是递增函数,则 在区间 上也是递增函数.
④若偶函数 在区间 上是递增函数,则 在区间 上是递减函数.
⑤函数 的图象是把函数 的图象沿x轴向左平移a个单位得到的;函数 ( 的图象是把函数 的图象沿x轴向右平移 个单位得到的;
函数 +a 的图象是把函数 助图象沿y轴向上平移a个单位得到的;函数 +a 的图象是把函数 助图象沿y轴向下平移 个单位得到的.
12、求一个函数的解析式和一个函数的反函数时,你标注了该函数的定义域了吗?
13、求函数的定义域的常见类型记住了吗?函数y= 的定义域是;
复合函数的定义域弄清了吗?函数 的定义域是[0,1],求 的定义域.函数 的定义域是[ ], 求函数 的定义域
14、一个函数的奇偶性时,你注意到函数的定义域是否关于原点对称这个必要非充分条件了吗?在公共定义域内:两个奇函数的乘积是偶函数;两个偶函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数;
15、据定义证明函数的单调性时,规范格式是什么?(取值,作差,判正负.)可别忘了导数也是判定函数单调性的一种重要方法。
16、函数 的单调区间吗?(该函数在 和 上单调递增;在
和 上单调递减)这可是一个应用广泛的函数!
17、函数问题时,你注意到真数与底数的限制条件了吗?(真数大于零,底数大于零且不等于1)字母底数还需讨论呀.
18、换底公式及它的变形,你掌握了吗?( )
19、你还记得对数恒等式吗?( )
20、“实系数一元二次方程 有实数解”转化为“ ”,你是否注意到必须 ;当a=0时,“方程有解”不能转化为 .若原题中没有指出是“二次”方程、函数或不等式,你是否考虑到二次项系数可能为零的情形?
二、三角、不等式
21、三角公式记住了吗?两角和与差的公式________________;二倍角公式:________________;解题时本着“三看”的基本原则来进行:“看角,看函数,看特征”,基本的技巧有:巧变角,公式变形使用,化切割为弦,用倍角公式将高次降次,
22、在解三角问题时,你注意到正切函数、余切函数的定义域了吗?正切函数在整个定义域内是否为单调函数?你注意到正弦函数、余弦函数的有界性了吗?
23、在三角中,你知道1等于什么吗?(
这些统称为1的代换)常数“1”的种种代换有着广泛的应用.(还有同角关系公式:商的关系,倒数关系,平方关系;
诱导公试:奇变偶不变,符号看象限)
24、在三角的恒等变形中,要特别注意角的各种变换.(如 等)
25、你还记得三角化简题的要求是什么吗?项数最少、函数种类最少、分母不含三角函数、且能求出值的式子,一定要算出值来)
26、你还记得三角化简的通性通法吗?(切割化弦、降幂公式、用三角公式转化出现特殊角.异角化同角,异名化同名,高次化低次);你还记得降幂公式吗?cos2x=(1+cos2x)/2;sin2x=(1-cos2x)/2
27、你还记得某些特殊角的三角函数值吗?
( )
28、你还记得在弧度制下弧长公式和扇形面积公式吗?( )
29、辅助角公式: (其中 角所在的象限由a,b的符号确定, 角的值由 确定)在求最值、化简时起着重要作用.
30、三角函数(正弦、余弦、正切)图象的草图能迅速画出吗?能写出他们的单调区、对称轴,取最值时的x值的集合吗?(别忘了k Z)
三角函数性质要记牢。函数y= k的图象及性质:
振幅|A|,周期T= ,若x=x0为此函数的对称轴,则x0是使y取到最值的点,反之亦然,使y取到最值的x的集合为,当 时函数的增区间为,减区间为;当 时要利用诱导公式将 变为大于零后再用上面的结论。
五点作图法:令 依次为 求出x与y,依点 作图
31、三角函数图像变换还记得吗?
平移公(1)如果点P(x,y)按向量 平移至P′(x′,y′),则
(2)曲线f(x,y)=0沿向量 平移后的方程为f(x-h,y-k)=0
32、有关斜三角形的几个结论:(1) 正弦定理:(2) 余弦定理:(3)面积公式
33、在用三角函数表示直线的倾斜角、两条异面直线所成的角等时,你是否注意到它们各自的取值范围及意义?
①异面直线所成的角、直线与平面所成的角、向量的夹角的取值范围依次是 .
②直线的倾斜角、 到 的角、 与 的夹角的取值范围依次是 .
34、不等式的解集的规范书写格式是什么?(一般要写成集合的表达式)
35、分式不等式 的一般解题思路是什么?(移项通分,分子分母分解因式,x的系数变为正值,奇穿偶回)
36、含有两个绝对值的不等式如何去绝对值?(一般是根据定义分类讨论)
37、利用重要不等式 以及变式 等求函数的最值时,你是否注意到a,b (或a,b非负),且“等号成立”时的条件,积ab或和a+b其中之一应是定值?(一正二定三相等)
38、 (当且仅当 时,取等号);a、b、c R, (当且仅当 时,取等号);
39、在解含有参数的不等式时,怎样进行讨论?(特别是指数和对数的底 或 )讨论完之后,要写出:综上所述,原不等式的解集是…….
40、解含参数的不等式的通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”
41、对于不等式恒成立问题,常用的处理方式?(转化为最值问题)
三、数列
42、等差数列中的重要性质:(1)若 ,则 ;(2) ;
(3)若三数成等差数列,则可设为a-d、a、a+d;若为四数则可设为a- 、a- 、a+ 、a+ ;
(4)在等差数列中,求Sn的最大(小)值,其思路是找出某一项,使这项及它前面的项皆取正(负)值或0,而它后面各项皆取负(正)值,则从第一项起到该项的各项的和为最大(小).即:当a1>0,d<0,解不等式组an≥0an+1≤0可得Sn达最大值时的n的值;当a1<0,d>0,解不等式组an≤0an+1≥0可得Sn达最小值时的n的值;(5).若an,bn是等差数列,Sn,Tn分别为an,bn的前n项和,则 。.(6).若{ }是等差数列,则{ }是等比数列,若{ }是等比数列且 ,则{ }是等差数列.
43、等比数列中的重要性质:(1)若 ,则 ;(2) , , 成等比数列
44、你是否注意到在应用等比数列求前n项和时,需要分类讨论.( 时, ; 时, )
45、等比数列的一个求和公式:设等比数列 的前n项和为 ,公比为 , 则
.
46、等差数列的一个性质:设 是数列 的前n项和, 为等差数列的充要条件是
(a,b为常数)其公差是2a.
47、你知道怎样的数列求和时要用“错位相减”法吗?(若 ,其中 是等差数列, 是等比数列,求 的前n项的和)
48、用 求数列的通项公式时,你注意到 了吗?
49、你还记得裂项求和吗?(如 .)
四、排列组合、二项式定理
50、解排列组合问题的依据是:分类相加,分步相乘,有序排列,无序组合.
51、解排列组合问题的规律是:相邻问题捆绑法;不邻问题插空法;多排问题单排法;定位问题优先法;多元问题分类法;有序分配问题法;选取问题先排后排法;至多至少问题间接法,还记得什么时候用隔板法?
52、排列数公式是:组合数公式是:排列数与组合数的关系是:
组合数性质: = + = =
二项式定理:
二项展开式的通项公式:
五、立体几何
53、有关平行垂直的证明主要利用线面关系的转化:线//线 线//面 面//面,线⊥线 线⊥面 面⊥面,垂直常用向量来证。
54、作出二面角的平面角主要方法是什么?(定义法、三垂线法)三垂线法:一定平面,二作垂线,三作斜线,射影可见.
55、二面角的求法主要有:解直角三角形、余弦定理、射影面积法、法向量
56、求点到面的距离的常规方法是什么?(直接法、等体积变换法、法向量法)
57、你记住三垂线定理及其逆定理了吗?
58、有关球面上两点的球面距离的求法主要是找球心角,常常与经度及纬度联系在一起,你还记得经度及纬度的含义吗?(经度是面面角;纬度是线面角)
59、你还记得简单多面体的欧拉公式吗?(V+F-E=2,其中V为顶点数,E是棱数,F为面数),棱的两种算法,你还记得吗?(①多面体每面为n边形,则E= ;②多面体每个顶点出发有m条棱,则E= )
六、解析几何
60、设直线方程时,一般可设直线的斜率为k,你是否注意到直线垂直于x轴时,斜率k不存在的情况?(例如:一条直线经过点 ,且被圆 截得的弦长为8,求此弦所在直线的方程。该题就要注意,不要漏掉x+3=0这一解.)
61、定比分点的坐标公式是什么?(起点,中点,分点以及 值可要搞清)
线段的定比分点坐标公式
设P(x,y),P1(x1,y1),P2(x2,y2),且 ,则
中点坐标公式
62、若 ,则△ABC的重心G的坐标是 在利用定比分点解题时,你注意到 了吗?
63、在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中一般提到的两条直线可以理解为它们不重合.
64、直线方程的几种形式:点斜式、斜截式、两点式、截矩式、一般式.以及各种形式的局限性.(如点斜式不适用于斜率不存在的直线)
65、对不重合的两条直线 , ,有:
; .
66、直线在坐标轴上的截矩可正,可负,也可为0.
67、直线在两坐标轴上的截距相等,直线方程可以理解为 ,但不要忘记当a=0时,直线y=kx在两条坐标轴上的截距都是0,也是截距相等.
68、两直线 和 的距离公式d=——————————
69、直线的方向向量还记得吗?直线的方向向量与直线的斜率有何关系?当直线L的方向向量为 =(x0,y0)时,直线斜率k=———————;当直线斜率为k时,直线的方向向量 =—————
70、到角公式及夹角公式———————,何时用?
71、处理直线与圆的位置关系有两种方法:(1)点到直线的距离;(2)直线方程与圆的方程联立,判别式. 一般来说,前者更简捷.
72、处理圆与圆的位置关系,可用两圆的圆心距与半径之间的关系.
73、在圆中,注意利用半径、半弦长、及弦心距组成的直角三角形并且要更多联想到圆的几何性质.
74、在利用圆锥曲线统一定义解题时,你是否注意到定义中的定比的分子分母的顺序?两个定义常常结伴而用,有时对我们解题有很大的帮助,有关过焦点弦问题用第二定义可能更为方便。(焦半径公式:椭圆:|PF1|=————;|PF2|=————;双曲线:|PF1|=————;|PF2|=————(其中F1为左焦点F2为右焦点);抛物线:|PF|=|x0|+ )
75、在用圆锥曲线与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零?判别式 的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在 下进行).
76、椭圆中,a,b,c的关系为————;离心率e=————;准线方程为————;焦点到相应准线距离为————双曲线中,a,b,c的关系为————;离心率e=————;准线方程为————;焦点到相应准线距离为————
77、通径是抛物线的所有焦点弦中最短的弦.
78、你知道吗?解析几何中解题关键就是把题目中的几何条件代数化,特别是一些很不起眼的条件,有时起着关键的作用:如:点在曲线上、相交、共线、以某线段为直径的圆经过某点、夹角、垂直、平行、中点、角平分线、中点弦问题等。圆和椭圆参数方程不要忘,有时在解决问题时很方便。数形结合是解决解几问题的重要思想方法,要记得画图分析哟!
79、你注意到了吗?求轨迹与求轨迹方程有区别的。求轨迹方程可别忘了寻求范围呀!
80、在解
更多阅读

方差公式及计算器如何算方差 方差计算器
若x1,x2,x3......xn的平均数为m则方差s^2=1/n[(x1-m)^2+(x2-m)^2+.......+(xn-m)^2]方差即偏离平方的均值,称为标准差或均方差,方差描述波动程度。MODE 2进入SD模式。统计前要先清除上次统计纪录:SHIFTAC=。然后输入

MC34063芯片设计的计算公式及应用讲解 34063芯片
在论坛经常看到有人在应用MC34063的时候会遇到这样那样的问题,特别的电路中的参数计算上很是不太明了,我会陆续贴上一些相关的计算公式及相关应用数据,欢迎大家参与讨论。外围元件标称含义和它们取值的计算公式:Vout(输出电压)=1.25V(1+R
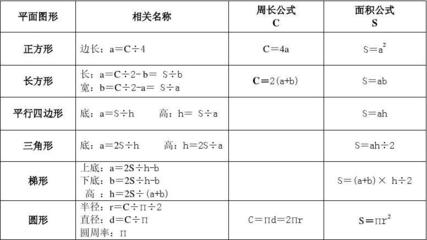
小学数学公式及数学换算公式 小学换算公式大全
长度单位换算1千米=1000米 1米=10分米1分米=10厘米 1米=100厘米1 厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算
较全的同花顺公式用函数 - 指标公式及技术交流区 - 理想论坛 - 中 同花顺积突指标公式
较全的同花顺公式用函数本文来自:理想论坛 www.55188.com 作者:天河饮马 点击112次原文:http://www.55188.com/viewthread.php?tid=3363908 我所知道的“同花顺”函数,不一定是全部,我也没有全部试用过。CLOSE含义:当周期的收盘价。用于:个
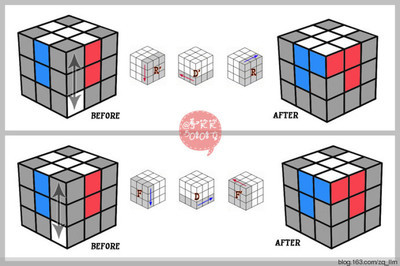
转载 七步玩转三阶魔方还原公式及非公式步骤图解新手适用超详 魔方公式七步法图解
原文地址:七步玩转三阶魔方还原公式及非公式步骤图解【新手适用超详细】作者:荞麦花开高中的时候受同桌的影响,非常痴迷魔方,上课的时候不停地偷偷转魔方练手,连走路的时候也一定要转着魔方。常常和同桌交换各自的公式,交流心得,那段时光真
 爱华网
爱华网