二阶系统的标准形式为:
C(s)/G(s)=wn^2/s^2+2*wn*zeta*s+wn^2;
利用matlab仿真分析zeta取不同值时的单位阶跃响应程序如下:
clear clf
wn=2;
t=0:0.01:20
for zeta=[0:0.2:1.2]
s=tf(4,[1,4*zeta,4]);
figure(1),step(s,t),hold on
end
grid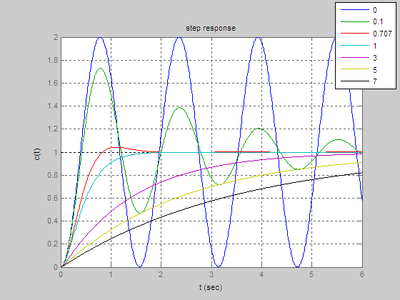
title('二阶系统响应取不同阻尼比时的单位阶跃响应')
gtext('zeta=0');gtext('zeta=0.2');gtext('zeta=0.4');gtext('zeta=0.6');gtext('zeta=0.8');gtext('zeta=1');gtext('zeta=1.2');
hold off
仿真结果:
由上图可知:
当zeta=0时二阶系统无阻尼单位阶跃响应为平均值为1的等幅震荡。其振荡频率为wn,即为无阻尼振荡。
当0<zeta<1时二阶系统为欠阻尼二阶系统,其单位阶跃响应为衰减振荡,
当zeta=1时二阶系统为临界阻尼二阶系统,其单位阶跃响应为稳态为1的无超调的单调上升过程。
当zeta>1时二阶系统为过阻尼二阶系统,其单位阶跃响应为是非振荡的。
在过阻尼和临界阻尼的响应曲线中,临界阻尼响应具有最短的上升时间,响应速度最快。在欠阻尼响应曲线中,阻尼比越小,超调量越大,上升时间越短,在zeta=0.4-0.8时超调量适度,调节时间较短,故通常zeta可在此范围内的选取。
 爱华网
爱华网