知识网络:
概念、定义:
1、 大于0的数叫做正数(positive number)。
2、 在正数前面加上负号“-”的数叫做负数(negative number)。
3、 整数和分数统称为有理数(rational number)。
4、 人们通常用一条直线上的点表示数,这条直线叫做数轴(number axis)。
5、 在直线上任取一个点表示数0,这个点叫做原点(origin)。
6、 一般的,数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value)。
7、 由绝对值的定义可知:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。
8、 正数大于0,0大于负数,正数大于负数。
9、 两个负数,绝对值大的反而小。
10、 有理数加法法则
(1) 同号两数相加,取相同的符号,并把绝对值相加。
(2) 绝对值不相等的异号两数相加,取绝对值较大的加数的负号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0。
(3) 一个数同0相加,仍得这个数。
11、 有理数的加法中,两个数相加,交换交换加数的位置,和不变。
12、 有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
13、 有理数减法法则
减去一个数,等于加上这个数的相反数。
14、 有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值向乘。
任何数同0相乘,都得0。
15、 有理数中仍然有:乘积是1的两个数互为倒数。
16、 一般的,有理数乘法中,两个数相乘,交换因数的位置,积相等。
17、 三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
18、 一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
19、 有理数除法法则
除以一个不等于0的数,等于乘这个数的倒数。
20、 两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0。
21、 求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂(power)。在an 中,a叫做底数(base number),n叫做指数(exponeht)
22、 根据有理数的乘法法则可以得出
负数的奇次幂是负数,负数的偶次幂是正数。
显然,正数的任何次幂都是正数,0的任何次幂都是0。
23、 做有理数混合运算时,应注意以下运算顺序:
(1) 先乘方,再乘除,最后加减;
(2) 同级运算,从左到右进行;
(3) 如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
24、 把一个大于10数表示成a×10n 的形式(其中a是整数数位只有一位的数,n是正整数),使用的是科学计数法。
25、 接近实际数字,但是与实际数字还是有差别,这个数是一个近似数(approximate number)。
26、 从一个数的左边的第一个非0数字起,到末尾数字止,所有的数字都是这个数的有效数字(significant digit)
注:黑体字为重要部分
二:整式的加减
知识网络:
概念、定义:
1、 都是数或字母的积的式子叫做单项式(monomial),单独的一个数或一个字母也是单项式。
2、 单项式中的数字因数叫做这个单项式的系数(coefficient)。
3、 一个单项式中,所有字母的指数的和叫做这个单项式的次数(degree of a monomial)。
4、 几个单项的和叫做多项式(polynomial),其中,每个单项式叫做多项式的项(term),不含字母的项叫做常数项(constantly term)。
5、 多项式里次数最高项的次数,叫做这个多项式的次数(degree of a polynomial)。
6、 把多项式中的同类项合并成一项,叫做合并同类项。
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变。
7、 如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
8、 如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
9、 一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项。
三:一元一次方程
知识网络:
概念、定义:
1、 列方程时,要先设字母表示未知数,然后根据问题中的相等关系,写出还有未知数的等式——方程(equation)。
2、 含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程(linear equation with one unknown)。
3、 分析实际问题中的数量关系,利用其中的等量关系列出方程,是用数学解决实际问题的一种方法。
4、 等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
5、 等式的性质2:等式两边乘同一个数,或除以一个不为0的数,结果仍相等。
6、 把等式一边的某项变号后移到另一边,叫做移项。
7、 应用:行程问题:s=v×t 工程问题:工作总量=工作效率×时间
盈亏问题:利润=售价-成本 利率=利润÷成本×100%
售价=标价×折扣数×10% 储蓄利润问题:利息=本金×利率×时间
本息和=本金+利息
三:图形初步认识
知识网络:
概念、定义:
1、 我们把实物中抽象的各种图形统称为几何图形(geometric figure)。
2、 有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一平面内,它们是立体图形(solid figure)。
3、 有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一平面内,它们是平面图形(plane figure)。
4、 将由平面图形围成的立体图形表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图(net)。
5、 几何体简称为体(solid)。
6、 包围着体的是面(surface),面有平的面和曲的面两种。
7、 面与面相交的地方形成线(line),线和线相交的地方是点(point)。
8、 点动成面,面动成线,线动成体。
9、 经过探究可以得到一个基本事实:经过两点有一条直线,并且只有一条直线。
简述为:两点确定一条直线(公理)。
10、 当两条不同的直线有一个公共点时,我们就称这两条直线相交(intersection),这个公共点叫做它们的交点(point of intersection)。
11、 点M把线段AB分成相等的两条线段AM和MB,点M叫做线段AB的中点(center)。
12、 经过比较,我们可以得到一个关于线段的基本事实:两点的所有连线中,线段最短。简单说成:两点之间,线段最短。(公理)
13、 连接两点间的线段的长度,叫做这两点的距离(distance)。
14、 角∠(angle)也是一种基本的几何图形。
15、 把一个周角360等分,每一份就是1度(degree)的角,记作1°;把一度的角60等分,每一份叫做1分的角,记作1′;把1分的角60等分,每一份叫做1秒的角,记作1″。
16、 从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线(angular bisector)。
17、 如果两个角的和等于90°(直角),就是说这两个叫互为余角(complementary angle),即其中的每一个角是另一个角的余角。
18、 如果两个角的和等于180°(平角),就说这两个角互为补角(supplementary angle),即其中一个角是另一个角的补角
19、 等角的补角相等,等角的余角相等。
七年级数学第一学期期末测试卷五
班级 姓名 学号
一、填空题(每小题3分,共30分)
1. 数轴上在原点左边且离开原点2个单位的点所表示的数是 。
2.2004年12月21日的天气预报,北京市的最低气温为 – 3℃,武汉市的最低气温为5℃,这一天北京市的最低气温比武汉市的最低气温低 ℃
3.神州五号载人飞船的成功发射,标志着我国向月球发射环绕月球探测卫星的条件已渐成熟。月球距地球约为38万千米,用科学记数法表示为 。
4.关于x的方程ax = x + a的解是x = 3,则a的值是 。
5.七年级(1)班数学兴趣小组的同学一起租车秋游,预计租车费人均摊1 5元,后来又有4名同学加入进来,租车费不变,结果每人可少摊3元,设原来有学生x人,可列方程为 。
6.如图是某晚报“热线电话”一周内接到的热线电话的统计图,这周内一共接到热线电话 个。
(第6题图) (第10题图)
7.计算:36°27′×3 = 。
8.已知点C是线段AB的中点,点D是AB的一个三等分点,且AB = 24cm,则CD = cm。
9.时钟上7点整时,时针和分针的夹角是 度。
10.如图,∠AOC =∠BOD = 90°, 且∠AOB = 162°,则∠COD = 度。
二、选择题(每小题3分,共18分)在每小题给出的四个选项中,只有一个是正确的。
11.式子6 + x与x + 1的和是31,则x的值是( )
A.– 12 B.12 C.13 D.– 19
12.若有理数a、b满足ab>0,且a + b<0,则下列说法正确的是( )
A.a、b可能一正一负
B.a、b都是正数
C.a、b都是负数
D. a、b中可能有一个为0
13.为了节约用水,某市规定:每户居民每月用水不超过15立方米,按每立方米1.6元收费,超过15立方米,则超过部分按每立方米2.4元收费。小明家六月份交水费33. 6元,则小明家六月份实际用水( )立方米
A.21 B.20 C.19 D.18
14.下列图形中,不是正方体表面展开图的图形的个数是( )
A.1个 B.2个 C.3个 D.4个
15.如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF = 60°,则∠DAE =( )
(第15题图) (第16题图)
A.15° B.30° C.45° D.60°
16.观察图形,下列说法正确的个数是( )
(1)直线BA和直线AB是同一条直线;
(2)射线AC和射线AD是同一条射线;
(3)AB + BD >AD;
(4)三条直线两两相交时,一定有三个交点;
A.1个 B.2个 C.3个 D.4个
三、解答题(本大题共52分)
17.(本题5分)
计算:
18.(本题5分)
解方程:7x + 6 = 16 – 3x
19.(本题共8分,每小题4分)
(1)在直线l上顺次取A、B、C三点,使得AB = 4cm,BC = 3cm。如果O是线段AC的中点,求线段OB的长度。
(2)已知∠α的余角等于15°,求∠α的补角。
20.(本题6分)
小虫从某点O出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位:厘米)依次为:+ 5、– 3、+ 10、– 8、– 6、+ 12、– 10。
(1)通过计算说明小虫是否回到起点;
(2)如果小虫爬行的速度为0.5厘米/秒,小虫共爬行了多少时间?
21.(本题6分)
如图,∠AOB = 110°,∠COD = 70°,OA平分∠EOC,OB平分∠DOF,求∠EOF的大小。
22.(本题6分)
一家公司的市场调查员对本公司的售后服务情况进行了调查,调查结果如下表。
(1)该公司一共调查了 人,其中满意(包括很满意和比较满意)的人数占被调查人数的百分比是 ;
(2)请将调查结果制成统计图;
(3)请你向公司提出一点建议。
类别
人数
很满意
70
比较满意
105
不满意
40
很不满意
35
合计
23.(本题6分)
一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装的成本价是多少元?
24..(本题10分)
(1)已知 ∠BOC = 120°,∠AOB = 70°,求 ∠AOC的大小;
(2)已知∠AOB = 80°,过O作射线OC(不同于OA、OB),满足∠AOC = ∠BOC,求∠AOC的大小。
(注:本大题中所说的角都是指小于平角的角)
参考答案
一、填空题
题号
答案
1
– 2
2
8
3
3.8×1015
4
1.5
5
15x = 12(x + 4)
6
440
7
109°21′
8
4
9
150
10
18
二、选择题
题号
11
12
13
14
15
16
答案
B
C
C
B
A
C
三、解答题
17.
18.x = 1
19.(1)OB = 0.5cm;
(2)105°
20.(1)小虫回到了起点;
(2)小虫共爬行了108秒钟。
21.∠EOF = 150°
22.(1)250,70%
(2)略
(3)提一条即可。
23.设这种服装的成本价是x元,得
(1 + 40%)X·80% = X + 15
解得 X = 125
答:这种服装的成本价是125元。
24.
(1)∠AOC = 50°或170°;
(2)当OC落在∠AOB内部时,如下图①
图①
由∠AOC = ∠BOC得:
∠AOC = 80°× = 30°。
当OC落在∠AOB外部时,如下图②,反向延长OA、OB。
若OC落在∠BON内,此时∠AOC>∠BOC,而∠AOC = ∠BOC,这不可能,舍去。
若OC落在∠MOA内部时,则∠BOC –∠AOC = 80°,且∠AOC∶∠BOC = 3∶5,∠BOC = 200°>180°,舍去。
若OC落在∠MON内部时,此时,∠AOC +∠BOC = 360° – 80°= 280°,故∠AOC = 280° × = 105°。
综上所述,∠AOC = 30°或105°。
图②
七年级数学第一学期期末测试卷一
一、选择题: 班级 姓名 学号
1.下列图形中,能够折叠成正方体的是( )
2.若a是有理数,则4a与3a的大小关系是( )
A.4a>3a B.4a=3a C.4a<3a D.不能确定
3.下列各对数中互为相反数的是( )
A.32与-23 B.-23与(-2)3; C.-32与(-3)2 D.(-3×2)2与23×(-3)
4.已知某班有40名学生,将他们的身高分成4组,在160~165cm区间的有8名学生,那么这个小组的人数占全体的( )
A.10% B.15% C.20% D.25%
5.一个数的倒数的相反数是 ,这个数是( )
A. B. C.- D.-
6.为了了解1万台某种电视机的使用寿命,从中抽出10台进行测试, 下列叙述正确的是( )
A.1万台某种电视机是总体; B.每台电视机是个体;
C.10台电视机的使用寿命是样本; D.以上说法都不正确
7.当a<0,化简 ,得( )
A.-2 B.0 C.1 D.2
8.把27430按四舍五入取近似值,保留两个有数数字, 并用科学记数法表示应是( )
A.2.8×104 B.2.8×103 C.2.7×104 D.2.7×103
9.某养鱼专业户年初在鱼塘中投放了500条草鱼苗,6个月后从中随机捞取17条草鱼,称重如下:
草鱼质量(单位:千克)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
草鱼数量(单位:条)
2
3
2
3
4
1
1
1
估计这鱼塘中年初投放的500条草鱼此时的总质量大约为( )千克.
A.845 B.854 C.846 D.847
10.一条船在灯塔的北偏东 方向,那么灯塔在船的什么方向( )
A.南偏西 ; B.西偏南 ; C.南偏西 ; D.北偏东
11.若2x+3=5,则6x+10等于( )
A.15; B.16; C.17; D. 34
12.已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC等于( )
A.120° B.120°或60° C.30° D.30°或90°
13.某商店有两个进价不同的计算器都卖了80元,其中一个
赢利60%,另一个亏本20%,在这次买卖中,这家商店( )
A.不赔不赚; B.赚了10元;
C.赔了10元; D.赚了50元
14.城镇人口占总人口比例的大小表示
城镇化水平的高低,由下面统计图可知,
我国城镇化水平提高最快的时期是( )
A.1953年~1964年;B. 1964年~1982年;C. 1982年~1990年;D. 1990年~2002年;
二、填空题:
15.调查某城市的空气质量,应选择_______(填抽样或全面)调查.
16.若│x+2│+(y-3)2=0,则xy=____.
17.已知∠ =72°36′,则∠ 的余角的补角是_____度。
18.如图,∠AOC和∠BOD都是直角,如果∠DOC= ,则∠AOB=_ __.
19.观察下列数字的排列规律,然后在括号内填入适当的数:
3,-7,11, ,19,-23,( ),( ).
20.若线段AB=10cm,在直线AB上有一点C,且BC=4cm,M是线段AC的中点,则AM=______cm.
三、解答题:
21.已知一条射线OA,如果从点O再引两条射线OB和OC,使∠AOB=60°, ∠BOC=20°,
求∠AOC的度数.
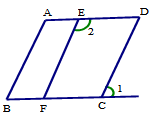
22.如图,直线AB与CD相交于点O,那么∠1=∠2吗?请说明你的理由.
23.计算:
(1) ; (2) .
24.解方程:
(1) ; (2) .
25.某果农承包了一片果林,为了了解整个果林的挂果情况, 果家随机抽查了部分果树挂果树进行分析.下图是根据这组数据绘制的统计图,图中从左到右各长方形之比为5:6:8:4:2,又知挂果数大于60的果树共有48棵.
(1)果农共抽查了多少棵果树?
(2)在抽查的果树中,挂果树在40~60之间的树 有多少棵,占百分之几?
26.“五一”长假日,弟弟和妈妈从家里出发一同去外婆家,他们走了1小时后,哥哥发现带给外婆的礼品忘在家里,便立刻带上礼品以每小时6千米的速度去追,如果弟弟和妈妈每小时行2千米,他们从家里到外婆家需要1小时45分钟,问哥哥能在弟弟和妈妈到外婆家之前追上他们吗?
27.某学校班主任暑假带领该班三好学生去旅游,甲旅行社说:“如果教师买全票一张,其余学生享受半价优惠。” 乙旅行社说:“教师在内全部按票价的6折优惠。” 若全部票价是240元。(1)如果有10名学生,应参加哪个旅行社,并说出理由。
(2)当学生人数是多少时,两家旅行社收费一样多?
28.某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售,每吨利润7000元。当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行。受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕。为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成。
如果你是公司经理,你会选择哪一种方案,说说理由。
答案:
一、选择题:C D C C D C A C C A B B B D
二、填空题:
15. 抽样调查;
16.-6
17.162.6
18.1440
19.27,-31;
20.3或7cm
三、解答题:
21.解:当OC在∠AOB的内部时,如答图(1),此时∠AOC=∠AOB-∠BOC=60°- 20°=40°.
当OC在∠AOB的外部时,如图(2),此时∠AOC=∠AOB+∠BOC=60°+20°=80°,
∴∠AOC等于40°或80°.
22.略.
23.(1) -12,(2) ;
24.(1) x=3, (2) ;
25.(1)200棵,(2)56%;
26. 解:设哥哥追上弟弟需要 小时,由题意得:
解这个方程得:
所以,弟弟行走了 小时小于1小时45分,未到外婆家,哥哥能够追上。
27. 解:(1)甲 240×10×0.5+240=1440
乙 240×(10+1)×0.6=1584
(2)设当学生人数为 x人时。
240·x·0.5+240=240(x+1) ·0.6
x=4
28. 解:方案一:4000×140=560000(元);
方案二:15×6×7000+(140-15×6)×1000=680000(元);
方案三:设精加工x吨,则
解得,x=60,
7000×60+4000×(140-60)=740000(元)
答:选择第三种。
七年级数学第一学期期末测试卷六
满分100分,考试时间120分.班级 姓名 学号
题 号
一
二
三
总 分
21
22
23
24
25
26
得 分
一、填空题(本大题共10小题,每小题3分,共30分.请将答案直接填入题后的横线上)
1.- 的相反数是 .
2.计算: = .
3.某种商品的零售价为m元,顾客以八折的优惠价购买此商品,共需付款 元.
4.若单项式 的系数是 ,次数是 ,则 的值等于 .
5.大于 而小于 的所有整数的和是 .
6.数轴上,A、B两点分别表示数-3、5,则A、B两点之间的距离是 .
7.在一个袋中放有5个红球和3个白球,把球摇匀后从袋中摸出一个球,则摸到 ___球的可能性大.
8.如果 , ,且 ,那么 .
9.已知:点B在线段AC上,AB=8cm,BC=12cm,M、N分别是AB、AC的中点,则MN= cm.
10.已知:∠AOB=35°,∠BOC=75°,则∠AOC= .
二、选择题(每小题3分,共30分.每小题给出的四个选项中,只有一项是符合题目要求的,
将正确结论的代号填入题后的括号内)
11.下列各数: , , , 中,负数有( )
(A)1个 (B)2个 (C)3个 (D)4个
12.我国研制的“曙光3000超级服务器”排在全世界运算速度最快的500台高性能计算机的第80位,它的峰值速度达到每秒403 200 000 000次,用科学记数法表示它的峰值计算速度为每秒( )
(A) 次 (B) 次
(C) 次 (D) 次
13.如果一个数的倒数是它本身,那么这个数是( )
(A)1 (B)-1 (C)0 (D)±1
14.下列式子正确的是( )
(A) (B)
(C) (D)
15.关于多项式 ,下列说法正确的是( )
(A)它是三次四项式 (B)它是关于字母 的降幂排列
(C)它的一次项是 (D) 与 是同类项
16.下列图形中,是正方体表面展开图的是( )
(A) (B) (C) (D)
17.某测绘装置上一枚指针原来指向南偏西55°,把这枚指针按逆时针方向旋转80°,
则结果指针的指向( )
(A)南偏东35o (B)北偏西35o
(C)南偏东25o (D)北偏西25o
18.若∠1与∠3互余,∠2与∠3互补,则∠1与∠2的
关系是( )
(A)∠1=∠2 (B)∠1与∠2互余
(C)∠1与∠2互补 (D)∠2-∠1=90°
19.直线a、b、c中,a∥b,a∥c,则直线b与直线c的
关系是( ) (第17题图)
(A)相交 (B)平行 (C)垂直 (D)不确定
20.如图是由一些相同的小正方体构成的立体图形的三种视图.那么构成这个立体图形的小正方体有( )
主视图 俯视图 左视图
(A)4个 (B)5个 (C)6个 (D)7个
三、计算(每小题6分,共18分)
21. .
22. .
23. ,其中 .
四、解下列各题(24、25小题每小题7分,26小题8分,共22分)
24.如图,已知:∠1=70°,∠2=70°,∠3=85°,求∠4的度数.
25.某储蓄代办员办理业务,约定存入为正,取出为负.某天他办理了6件业务:-780元、-650元、+1250元、-310元、-420元、+240元.
(1)若他早上领取备用金5000元,那么下班时应交回银行多少元?
(2)若每办一件业务,银行发给业务量的0.08%作为奖励,这天他应得奖金多少元?
26.美化城市,改善人们的居住环境已成为城市建设的一项重要内容。某市区近几年来,
通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加.
(1)根据图中所提供的信息,回答下列问题:2002年底的绿地面积为 公顷,比2001年底增加了 公顷;在2000年,2001年,2002年这三年中,绿地面积增加最多的是 年;
(2) 城区每年年底绿地面积统计图
1999
2000
2001
2002
60
56
51
48
年份
绿地面积(公顷)
为满足城市发展的需要,计划到2004年底使城区绿地总面积达到 公顷,试求2004年底绿地面积比2002年底增长了百分之几?
成功学校2004-2005学年度第一学期七年级期末考试
数学附加题
(本卷满分50分)
姓名 学号 得分 .
1.计算: .
2.已知三个有理数 , , 的积是负数,它们的和是正数,当 时,求代数式 的值.
3.解方程: .
4.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50﹪的利润定价,乙服装按40﹪的利润定价。在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
5.下面两幅统计图(如图1、图2),反映了某市甲、乙两所中学学生参加课外活动的情况.请你通过图中信息回答下面的问题.
甲校 乙校
图1 图2
(1)通过对图1的分析,写出一条你认为正确的结论;
(2)通过对图2的分析,写出一条你认为正确的结论;
(3)2003年甲、乙两所中学参加科技活动的学生人数共有多少?
参考答案
一、填空题
1. 2.2 3. 4.-2 5.-2 6.8 7.红 8.0 9.6 10.110°或40°.
二、选择题
11.B 12.C 13.D 14.D 15.B 16.C 17.C 18.D 19.B 20.B.
三、计算
21.-18.
22.43.
23. (3分),30(3分).

四、解下列各题
24.由已知条件可得∠1=∠2,根据同位角相等,
两直线平行,可得 ∥ .(4分)
因为 ∥ ,根据两直线平行,同旁内角互补,
可得∠3+∠4=180°,因此∠4=180°-85°=95°.(3分)
25.(1)5000-780-650+1250―310―420+240
=4330(元);(3分)
(2)(780+650+1250+310+420+240)×0.1%=3.65(元)(3分)
答:(1)他下班时应交回银行4330元;(2)这天他应得奖金为3.65元.(1分)
26.(1)60,4,2001;(每空2分)
(2) .
答:2004年底绿地面积比2002年底增长为21%.(2分)
 爱华网
爱华网